0.   引言

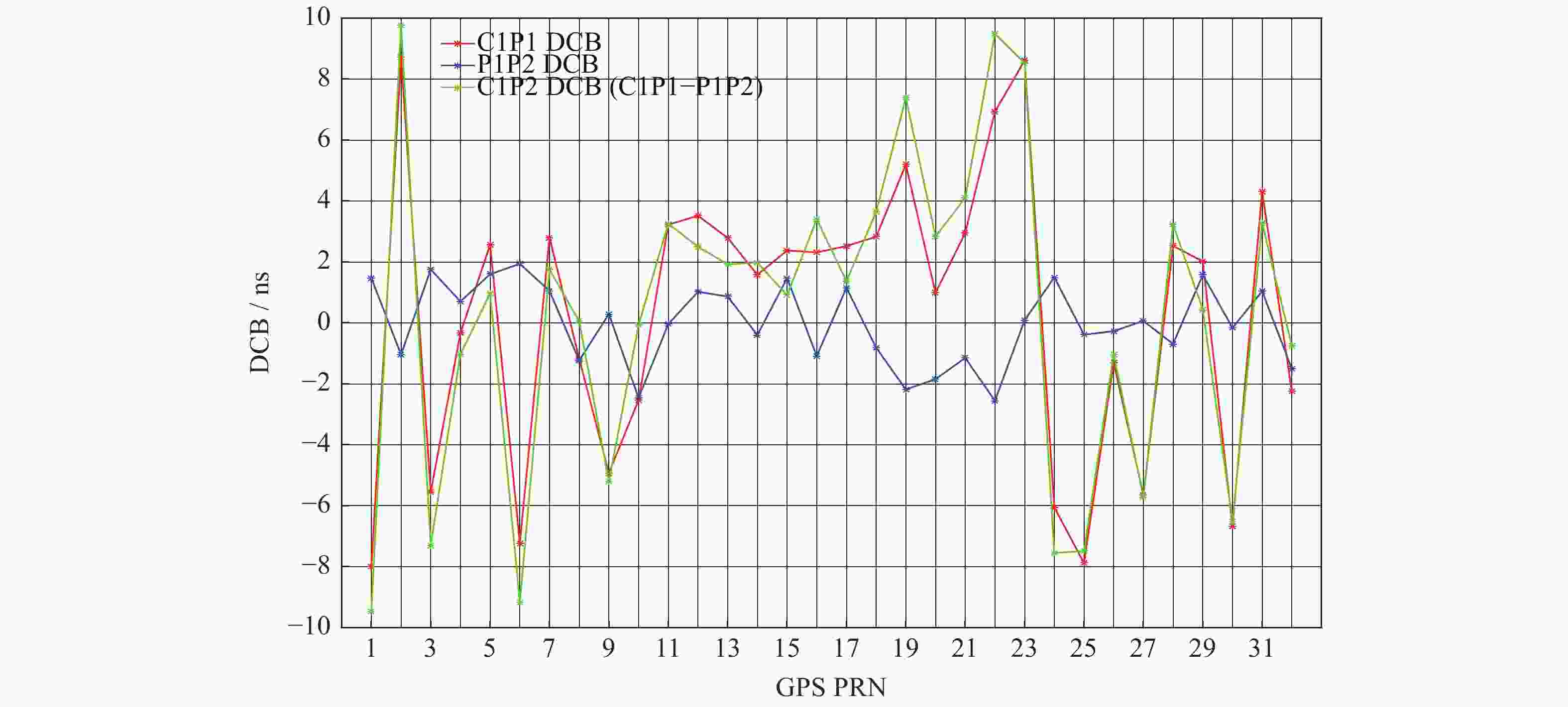
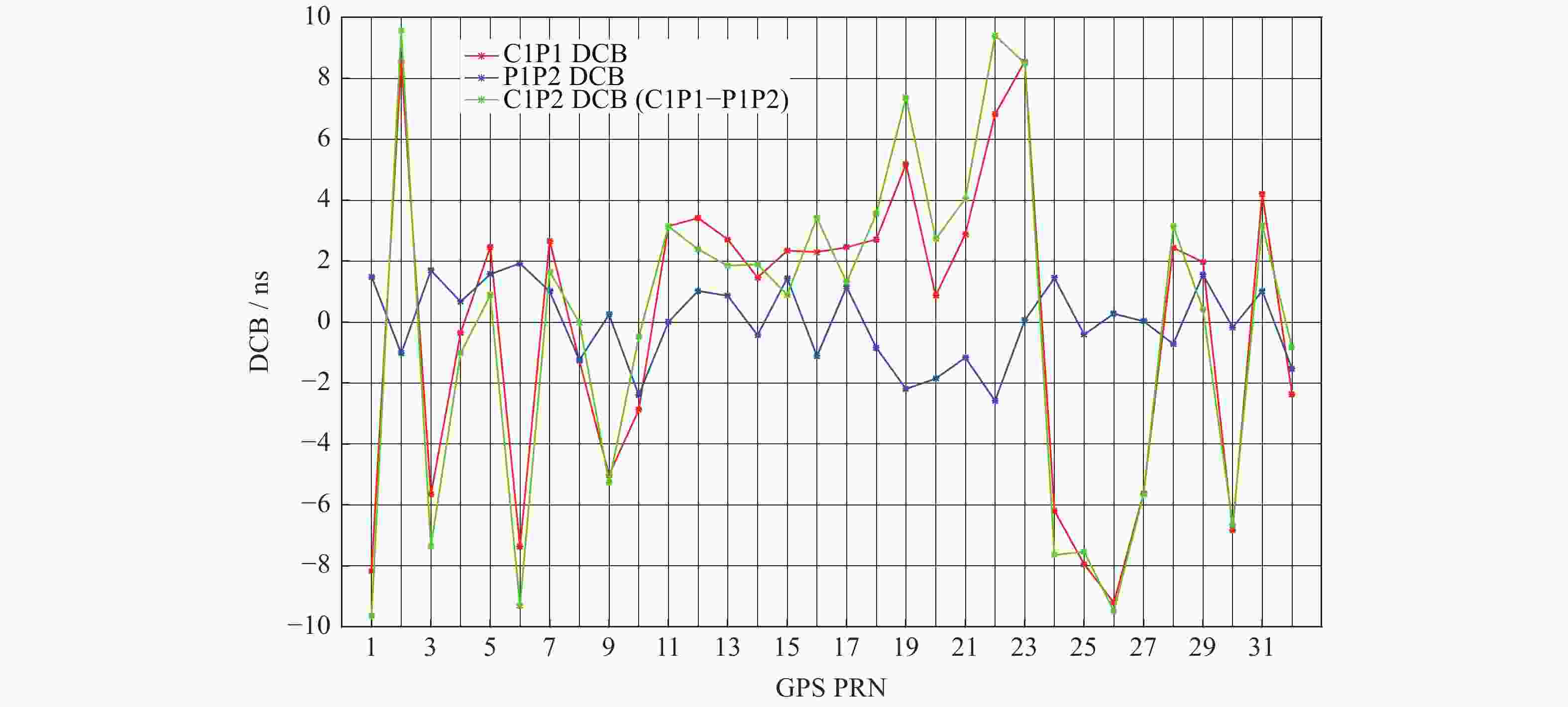
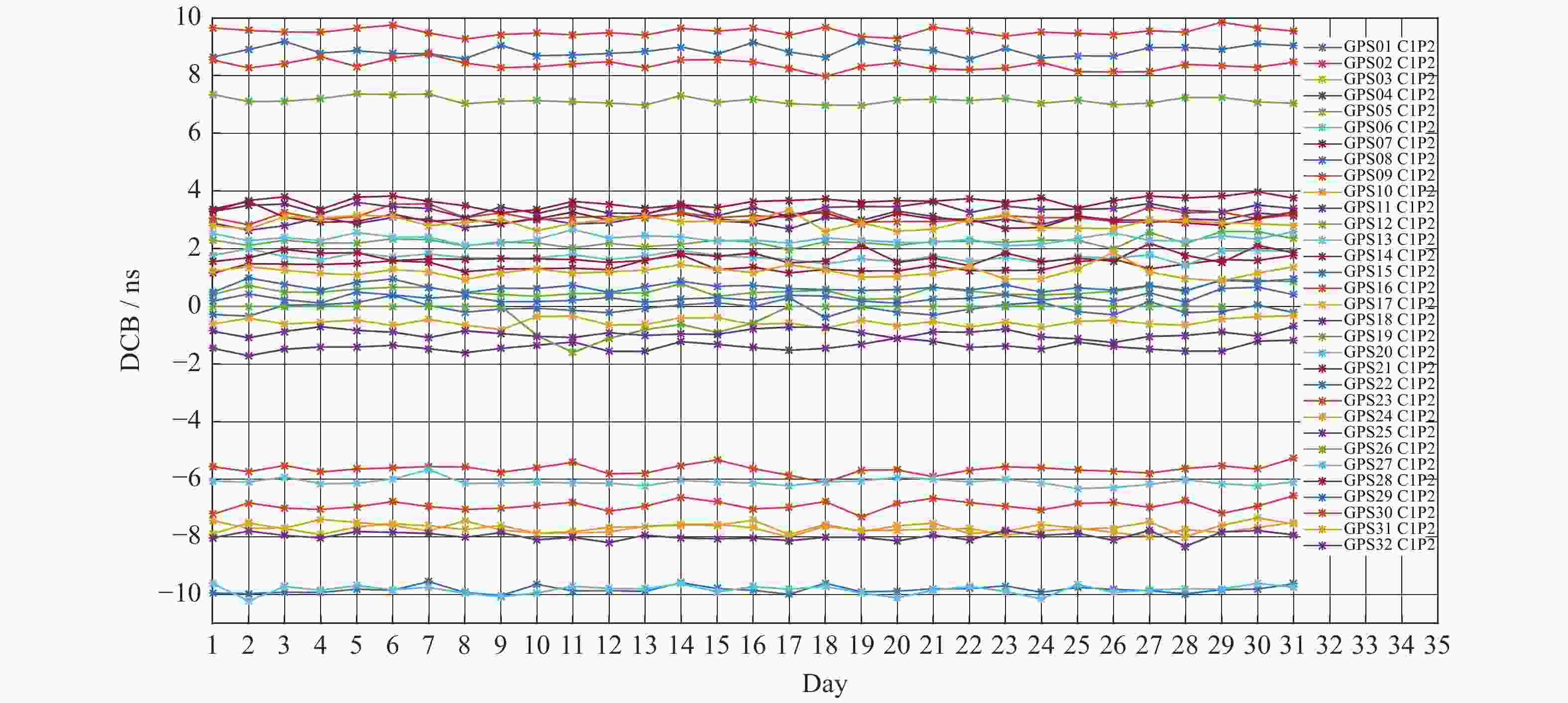
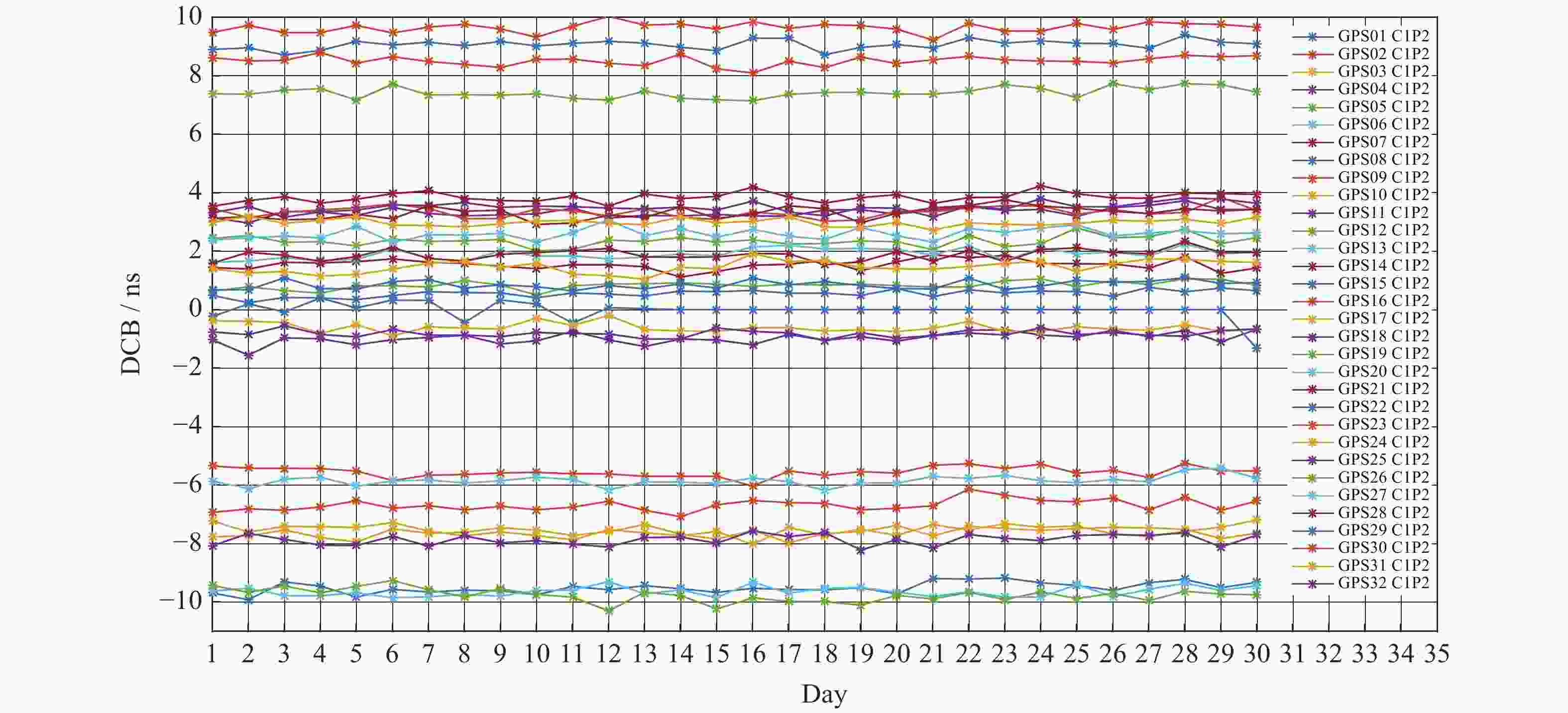
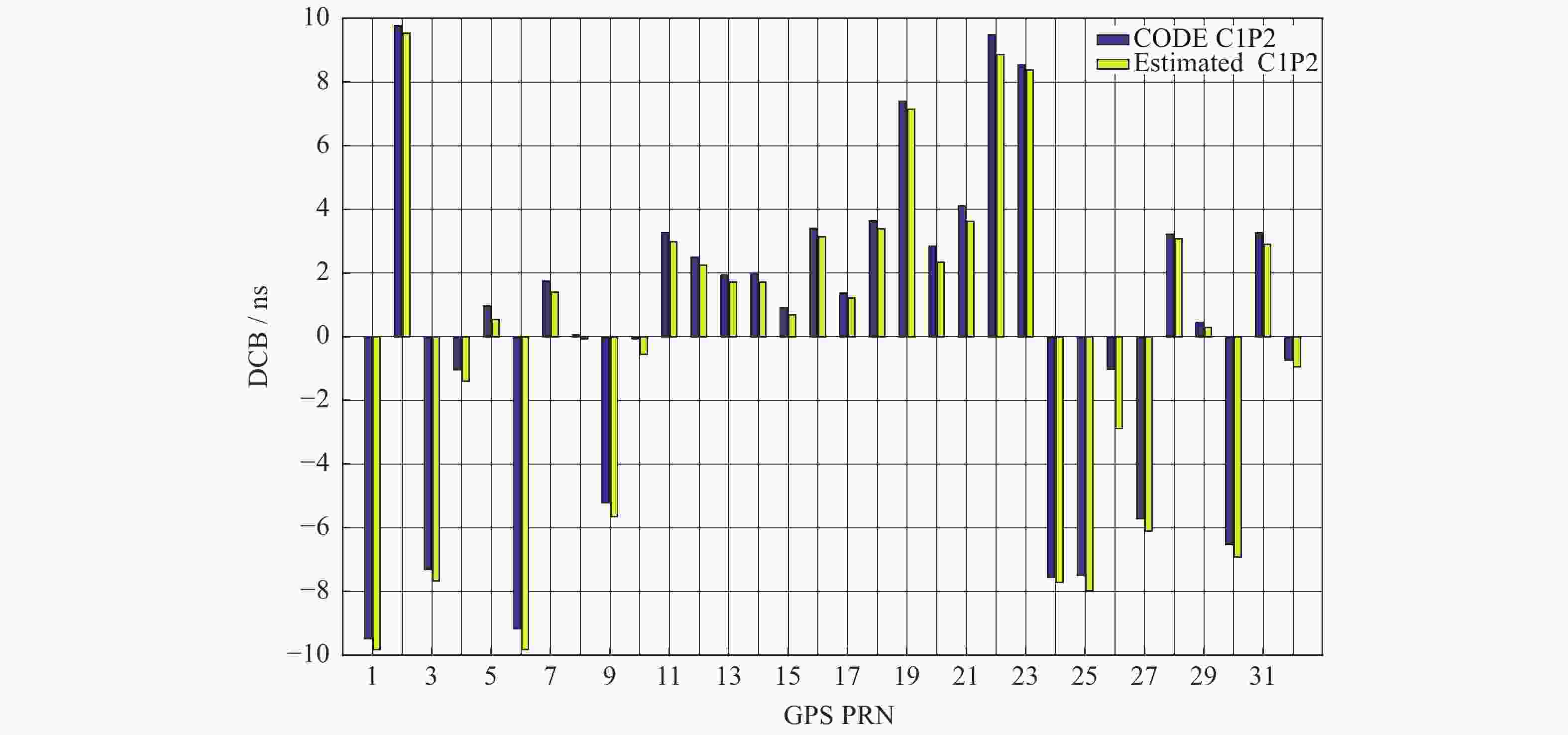
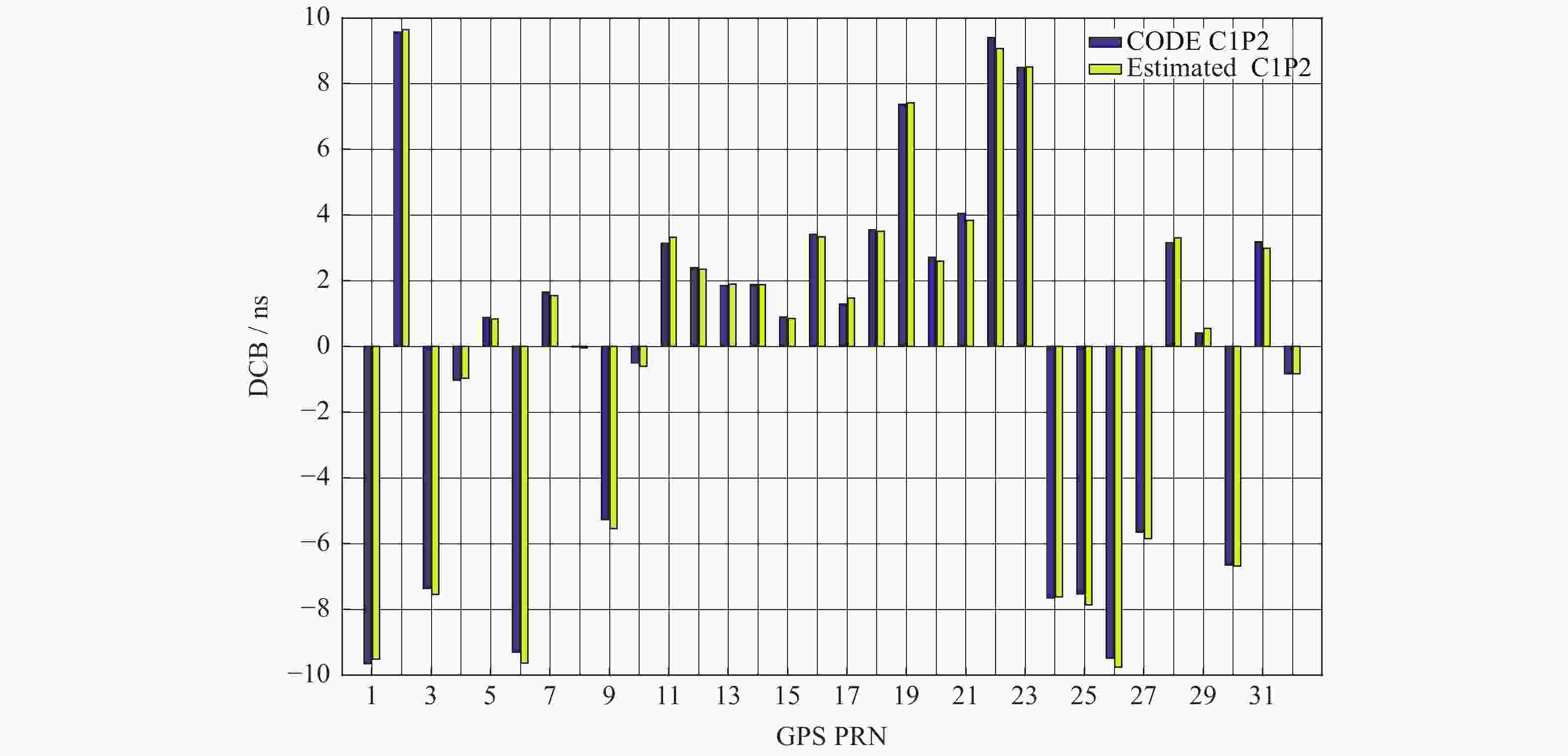
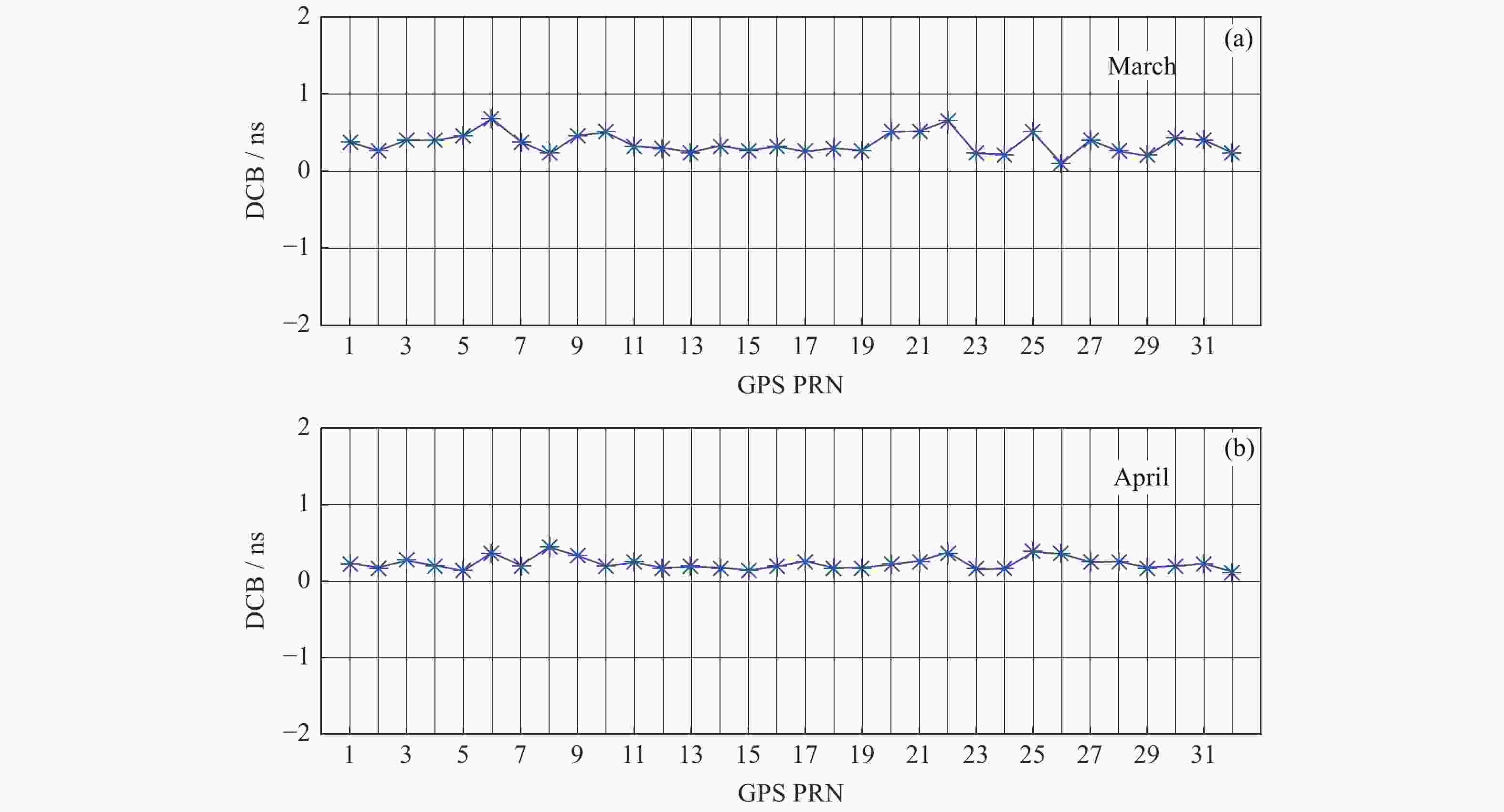
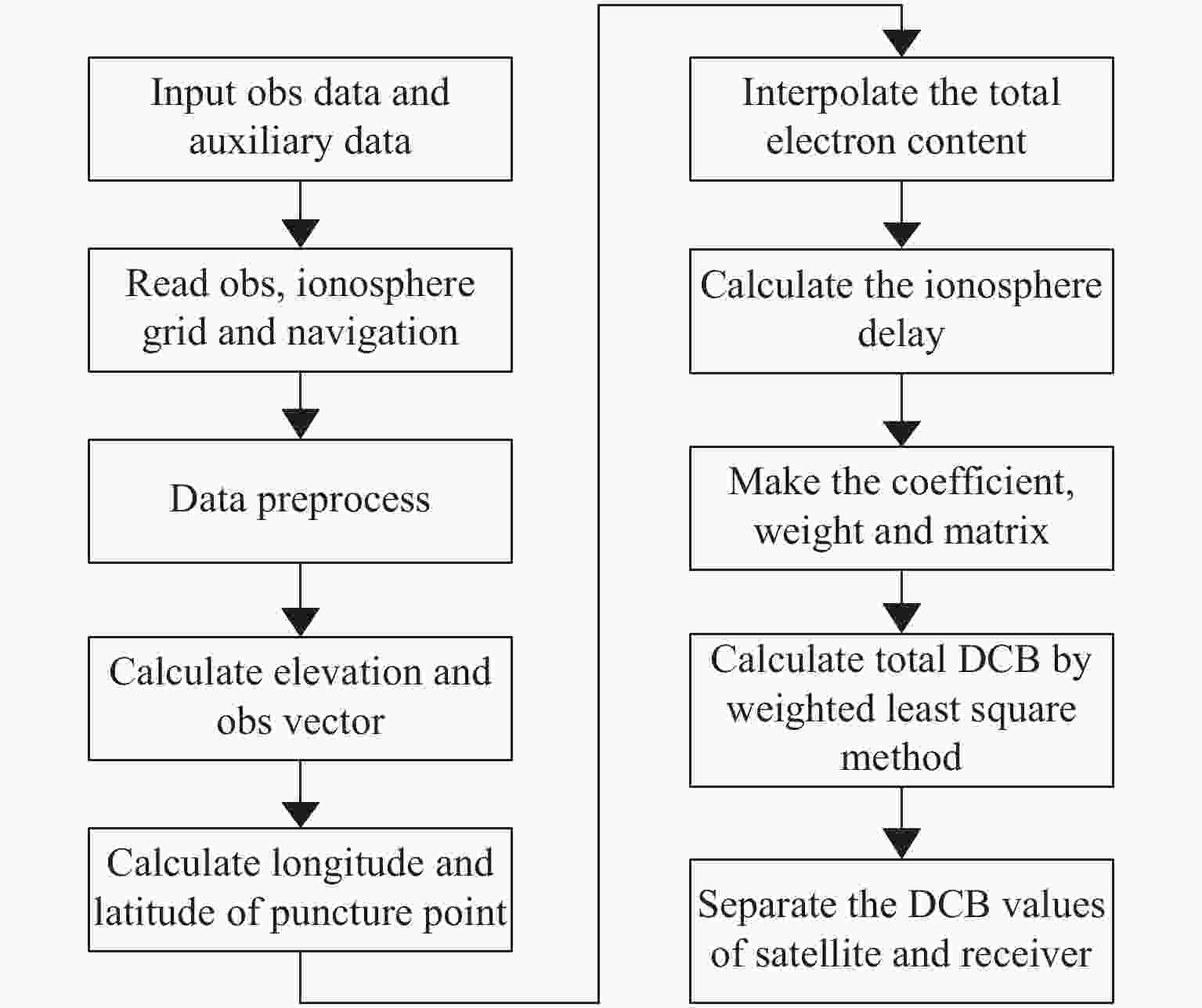
GNSS不同频点间的码伪距作差会引入信号的差分码偏差（DCB），GNSS卫星及地面接收机的DCB可以引起25 ns左右的精度误差，必须进行修正。差分码偏差修正在精密单点定位、星基电离层绝对TEC计算^[1,2]、地基VTEC计算等领域应用广泛。差分码偏差（DCB, Differential Code Bias）是由硬件延迟造成的相同历元下发射或接收不同频率GPS无线信号产生的频率间码偏差^[3]。在GPS无线信号传播路径上，发射端的卫星和地面接收机端均会产生一定码偏差^[4-6]。卫星码偏差（DCBs）可以通过欧洲定轨中心（Center for Orbit Determination in Europe, CODE）公布的结果得到；地面接收机码偏差（DCBr）可直接由公布的结果（例如IGS测站接收机的DCBr）或通过参数估计的方法得到。Lü等^[7]利用CODE中心下载的卫星DCB通过最小二乘法求解出了地面接收机的DCB。接收机硬件延迟会随着运行环境的不同而发生变化，其码偏差值可达±10.5 ns^[8]。DCB对于静态定位影响很小，而对于动态定位有厘米级的影响^[9]，故在电离层绝对TEC计算时必须要考虑GPS卫星和地面GNSS接收机DCB的影响。本文针对地面GNSS接收机在使用过程中无可用的接收机DCB参数公布问题，采用加权最小二乘法对DCB估算，并在试验数据上验证了估算方法的有效性。

1.   DCB算法实现

GNSS卫星及测站接收机DCB的计算主要有以下三种方法。

（1）利用CODE中心下载的所有GPS卫星DCB估计接收机DCB值。CODE数据中心会每月公布所有GPS卫星DCB值，借助这些值采用最小二乘法估计出测站接收机的DCB值。该方法的缺点是依赖于外部数据。

（2）载波相位平滑伪距法^[10]。载波相位非常平滑，具有较高的精度，用其平滑伪距能提高估计电离层电子总含量精度，从而实现DCB参数估计。该方法需要扣除钟差、多路径、对流层等误差影响，算法复杂性高。

（3）P₄双频伪距组合法^[11,12]。双频伪距组合能够消去与频率无关的钟差、多路径、对流层等误差影响，剩下卫星和接收机DCB以及电离层延迟影响，进而由参数估计能够得到GPS卫星和接收机DCB值。

本文在P₄双频伪距组合法^[13,15]基础上提出了一种地基GNSS接收机差分码偏差估算方法。算法中利用卫星的高度角进行加权，即使用高度角余角余弦值的平方作为权矩阵，同时通过加入20个IGS站的观测数据来实现观测卫星数据的覆盖性，从而更好地满足卫星DCB的零和条件。为了保证更多的卫星和数据加入运算，算法中设置高度角阈值为15º。GPS两个频率上的伪距观测量表达式分别为

式中：P₁和P₂为双频伪距观测量，其中数字作为下标表示频点；r为站星之间的距离；c为真空中的光速；δt_r为接收机钟差；δt^s 为卫星钟差；I₁和I₂分别为两个频率上的电离层延迟；T为对流层延迟；${N_{\varepsilon {p_1}}}$和${N_{\varepsilon {p_2}}}$为接收机噪声；两个频率上差分码偏差表示为$\psi _{r1}^{\rm{s}}$和$\psi _{r2}^{\rm{s}}$，表达式为

这里ψ_r1和ψ_r2分别表示GNSS接收机L1C频点和L2P频点上的码偏差，$\psi _1^{\rm{s}}$和$\psi _2^{\rm{s}}$分别表示GNSS卫星L1C频点和L2P频点上的码偏差。

P₄组合之后与频率无关的误差项被消去，忽略接收机噪声影响，只剩下电离层延迟和GPS卫星及接收机DCB延迟，表达式为

式中，τ_r和τ^s分别表示GNSS接收机和卫星差分码偏差，ε表示组合后的噪声。

电离层延迟通常采用单层模型（Single layer model），将电离层电子看成集中分布在离地400~450 km左右高度的一个单层球面上，通过导航电文和分布的多个接收机观测文件可以分别计算出卫星和接收机的位置，同时计算得到站星间的观测矢量和卫星的高度角及方位角，从而计算出电离层穿刺点的（Ionosphere Pierce Point, IPP）^[16,17]纬度和经度。依据IGS站下载的igsg电离层文件用线性插值法得到电离层穿刺点处的垂直总电子含量VTEC，求出投影函数即可计算出电离层延迟^[18,20]

式中，i=1,2表示频点，I_i表示i频点上的电离层延迟，z'表示卫星天顶角度，f_i表示i频点上频率大小，N_e表示电离层电子密度。

GPS导航定位中，卫星高度角在一定程度上反映数据质量的好坏，故选用卫星高度角信息来确定加权矩阵，使计算更接近实际情况，权阵表达式为

式中，P表示权矩阵，α表示卫星高度角，π为圆周率。

加权最小二乘法在解决重复观测问题上应用广泛^[21,23]，根据P₄组合组建系数矩阵 A，常数矩阵y，以及权重矩阵P，常数矩阵y通过组建的GNSS观测方程中各矩阵系数组成，GPS卫星和接收机的码偏差估计值为

2.   算法流程

DCB的计算过程主要包括参数文件的读取、电离层延迟计算和加权最小二乘估计等步骤。为方便估计全球范围内的GPS卫星和接收机DCB，选用brdc广播星历文件。为了能较准确地估计所有卫星的DCB值，选用除了待估计测站接收机外的尽可能多的IGS站观测数据，这样能够避免局部误差的影响。测试中随机选用20个全球分布的IGS站观测文件，使用本文研究成果同时估计GPS卫星和接收机DCB值，方便工程应用。

图1所示为GPS卫星和测站接收机DCB参数加权最小二乘估计算法流程，选用的数据是IGS站20个测站观测文件，历元间隔30 s一个，2015年3－4月连续两个月的数据。

图  1  DCB算法流程

Figure  1.  Flow chart of DCB algorithm

下载: 全尺寸图片 幻灯片

采用加权最小二乘准则进行计算，经统计一般迭代5~6次便会收敛，精度要求高的选择迭代10次，本文选则迭代10次。计算的DCB值是GPS卫星和测站接收机码偏差（DCB）之和，借助所有GPS卫星DCB之和为零^[24-29]这一条件分离出GPS卫星和测站接收机的DCB。

3.   数据结果分析

试验数据输入：待估算的2015年3月1日至4月30日时间段内的abpo、albh、alg3、baie、barh、bcov、bjco、cas1、eliz、escu、eur2、ganp、geno、gldr、glps、godz、guam、kiru、tid1、wes2等20个IGS站的GNSS观测数据文件，广播星历文件，电离层GIM数据文件，CODE中心P1P2和C1P1DCB文件。

利用CODE数据中心公布的GPS卫星的DCB与估算的GPS卫星的DCB进行对比分析本文方法的估计精度。从CODE数据中心下载了2015年3－4月的C1P1和P1P2码偏差值，通过对C1P2和P1P2进行作差可以得到C1P2码偏差值，结果分别如图2和图3所示。由图2和图3可知，GPS卫星的C1P2 DCB值差异性较大，在–10~10 ns范围内变动。对2015年3月和4月IGS测站连续两个月的观测数据进行分析，用本文研究成果计算GPS卫星的DCB值分别如图4和图5所示，横坐标day表示该月内的天数，纵坐标表示估算的C1P2 DCB数值，图中32种星线分别表示GPS 1~32卫星号PRN。从图4和图5中可知，一个月内GPS卫星的C1P2码偏差相对较稳定，变动范围在±1 ns以内。

图  2  CODE中心下载的2015年3月DCB数据

Figure  2.  DCB data for March 2015 downloaded from CODE Center

下载: 全尺寸图片 幻灯片

图  3  CODE中心下载的2015年4月DCB数据

Figure  3.  DCB data for April 2015 downloaded from CODE Center

下载: 全尺寸图片 幻灯片

图  4  估算的2015年3月卫星C1P2 DCB

Figure  4.  Estimated satellite C1P2 DCB in March 2015

下载: 全尺寸图片 幻灯片

图  5  估算的2015年4月卫星C1P2 DCB

Figure  5.  Estimated satellite C1P2 DCB in April 2015

下载: 全尺寸图片 幻灯片

与GPS卫星C1P2码偏差一同估算出来的还有测站接收机的C1P2码偏差值，其中估算的2015年3月和4月的abpo、albh、alg3、baie、barh、bcov、bjco、cas1、eliz、escu、eur2、ganp、geno、gldr、glps、godz、guam、kiru、tid1和wes2共20个测站的C1P2码偏差值分别如表1和表2所示。鉴于工程项目实践中使用的测站接收机的C1P2码偏差是未知的，使用测站接收机接收的观测数据代入进行估算，即可得到GPS卫星和测站接收机的C1P2码偏差。

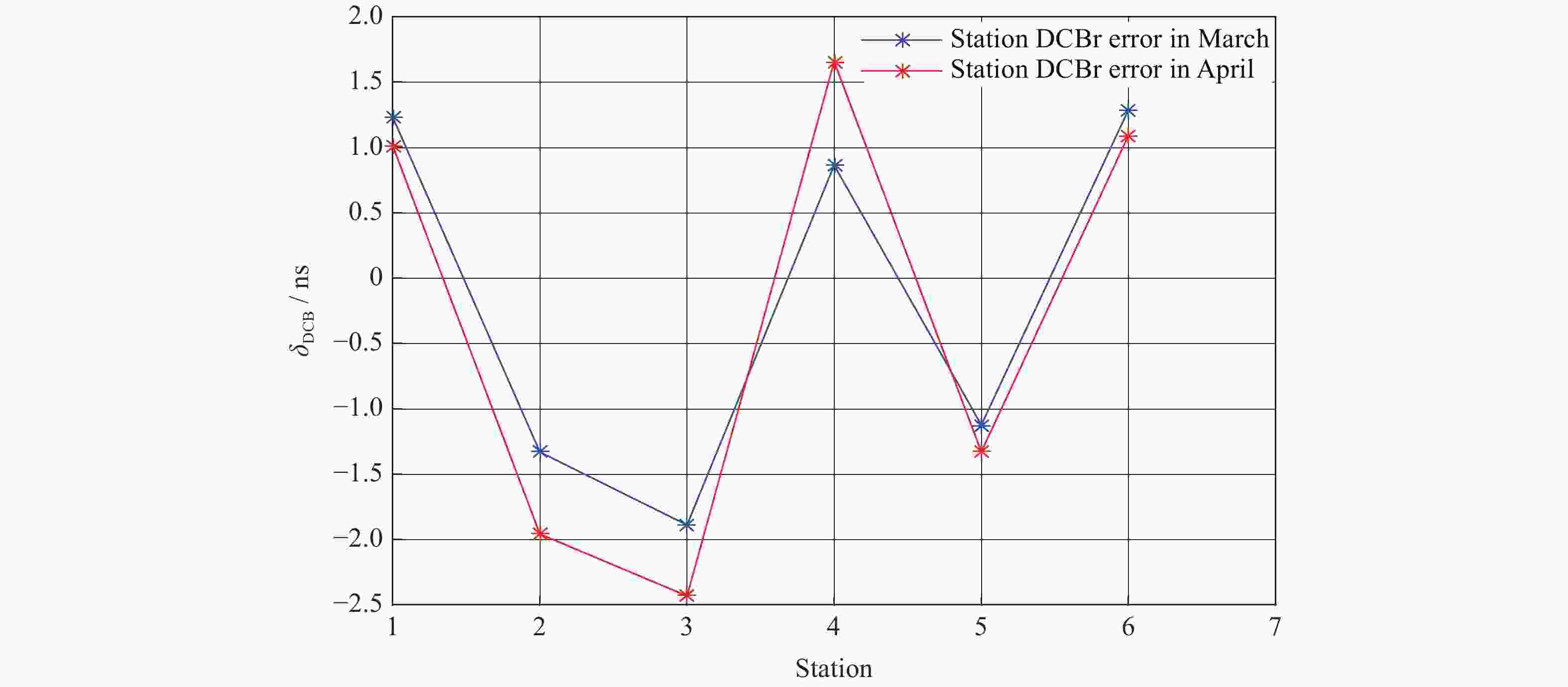
表  1  估算的2015年3月20个IGS站接收机码偏差值 （单位 ns）

Table  1.  Calculated receiver DCB for 20 IGS stations in March 2015 (Unit ns)

IGS站名	abpo	albh	alg3	baie	barh	bcov	bjco	cas1	eliz	escu
DCBr	–4.2823	11.1878	13.2729	9.1391	6.4724	5.8010	–12.6882	–7.6900	2.7586	–14.9059
IGS站名	eur2	ganp	geno	gldr	glps	godz	guam	kiru	tid1	wes2
DCBr	11.4201	–8.6954	21.420	4.6395	–0.5536	0.2306	6.1477	7.1547	–21.4409	11.0222

下载: 导出CSV 

| 显示表格

表  2  估算的2015年4月20个IGS站接收机码偏差值 （单位 ns）

Table  2.  Calculated receiver DCB for 20 IGS stations in April 2015 (Unit ns)

IGS站名	abpo	albh	alg3	baie	barh	bcov	bjco	cas1	eliz	escu
DCBr	–5.0597	11.0122	13.0821	9.0508	6.2674	5.9221	–13.2754	–8.0336	2.7610	–15.0996
IGS站名	eur2	ganp	geno	gldr	glps	godz	guam	kiru	tid1	wes2
DCBr	11.4382	–8.9486	21.4702	4.9973	–0.6551	0.1525	7.0748	7.0906	–21.5858	11.1649

下载: 导出CSV 

| 显示表格

为了评估估算出的GPS卫星C1P2码偏差和测站接收机C1P2码偏差的精度，利用CODE数据中心公布的C1P1和P1P2码偏差计算出的C1P2码偏差作为对比，2015年3月和4月的对比结果分别如图6和图7所示。由图6和图7可知，GPS 1~32号卫星的蓝色直方图和黄色直方图都较为接近。统计蓝色和黄色直方图之间的RMS误差如图8所示，GPS 1~32号卫星的C1P2码偏差的RMS误差为0.3541 ns。从CODE下载部分IGS站接收机的DCBr，与上述估算的测站接收机C1P2码偏差进行对比分析，IGS测站接收机C1P2码偏差通过公布的C1P1和P1P2码偏差计算得到（见表3），六个测站接收机C1P2估算精度如图9所示。由图9可知IGS六个测站接收机C1P2码偏差估算偏差基本在±2 ns以内。3月误差均值为–0.159 ns，RMS误差为1.4406 ns；4月误差均值为–0.3253 ns，RMS误差为1.7803 ns，RMS误差为1.6105 ns。本文使用的样本为2015年3－4月共61天的IGS观测数据，说明2015年的3－4月这段时间内GPS卫星DCB和地面接收机DCB精度在0.5 ns以内。需要说明的是，本文样本量略不足，使用该试验评价的结果可能具有片面性，其他时间段内DCB的估计精度可能需要进一步分析。另外，对于2015年3月17日出现的第24太阳活动周最强磁暴期间，从图8结果可以看出，卫星C1P2码偏差估算结果并没有出现太大偏差，分析其原因可能是因为采用的算法相近导致结果相差不大，还有可能是因为磁暴发生区域离选择的20个IGS站点距离较远从而没有受到影响。此外，由于CODE数据中心公布的DCBr也存在误差，本文评价的精度也存在一定的误差。

图  6  2015年3月CODE公布与估算的C1P2码偏差对比

Figure  6.  Comparison of the deviation between the CODE published in March 2015 and the estimated C1P2 code

下载: 全尺寸图片 幻灯片

图  7  2015年4月CODE公布与估算的C1P2码偏差对比

Figure  7.  Comparison of the deviation between the CODE published in April 2015 and the estimated C1P2 code

下载: 全尺寸图片 幻灯片

图  8  2015年3月和4月估算的卫星C1P2 DCB RMS误差

Figure  8.  Estimated Star C1P2 DCB RMS error in March and April 2015

下载: 全尺寸图片 幻灯片

表  3  下载的2015年3和4月6个IGS站接收机码偏差值 （单位 ns）

Table  3.  Download receiver DCBr for 6 IGS stations in March and April 2015 (Unit ns)

IGS站名		abpo	bjco	ganp	glps	tid1	godz
3月	P1 P2	–5.628	–14.647	–10.175	–1.804	–22.974	–2.234
	P1 C1	–0.113	–3.289	–3.368	–0.385	–2.656	–1.175
	C1 P2	–5.515	–11.358	–6.807	–1.419	–20.318	–1.059
4月	P1 P2	–5.894	–14.681	–9.989	–1.871	–22.917	–2.042
	P1 C1	0.180	–3.363	–3.472	0.442	–2.660	–1.101
	C1 P2	–6.074	–11.318	–6.517	–2.313	–20.257	–0.941

下载: 导出CSV 

| 显示表格

图  9  2015年3和4月估算的测站C1P2 DCBr误差

Figure  9.  Estimated Station C1P2 DCBr error in March and April 2015

下载: 全尺寸图片 幻灯片

4.   结语

由电离层文件参数作线性插值，计算出电离层延迟误差。对20个IGS站观测文件进行加权最小二乘法进行估计，得到GPS卫星和地面GNSS接收机的C1P2码偏差。估算的GPS卫星C1P2码偏差与CODE中心下载DCB之差的RMS误差为0.3541 ns，IGS 测站接收机的DCBr的RMS误差为1.6105 ns。在动态精密单点定位和绝对TEC计算过程中，本文研究成果能同时对GPS卫星和接收机C1P2码偏差进行估计。在获取多个IGS站和待测站接收机观测文件情况下，能估计出地面GNSS接收机的DCBr，提高电离层绝对TEC的计算精度。本文研究成果可以解决GNSS接收机出厂后DCBr无法更新或不准确的问题。在PPP定位和电离层绝对TEC计算等需要用到码间作差的工程应用中，具有重要的实用价值。另外，对于地震和磁暴期间地面GNSS接收机DCBr估算精度的研究还需要在大量样本基础上作进一步精细化研究。

致 谢　本文实验使用了CODE数据中心公布的GPS卫星DCB作为对比，同时使用了IGS网址的测站观测数据O文件、广播星历N文件和电离层格网igsg文件。