Effects of Sea Surface Temperature on the CFOSAT Scatterometer Measurements
-
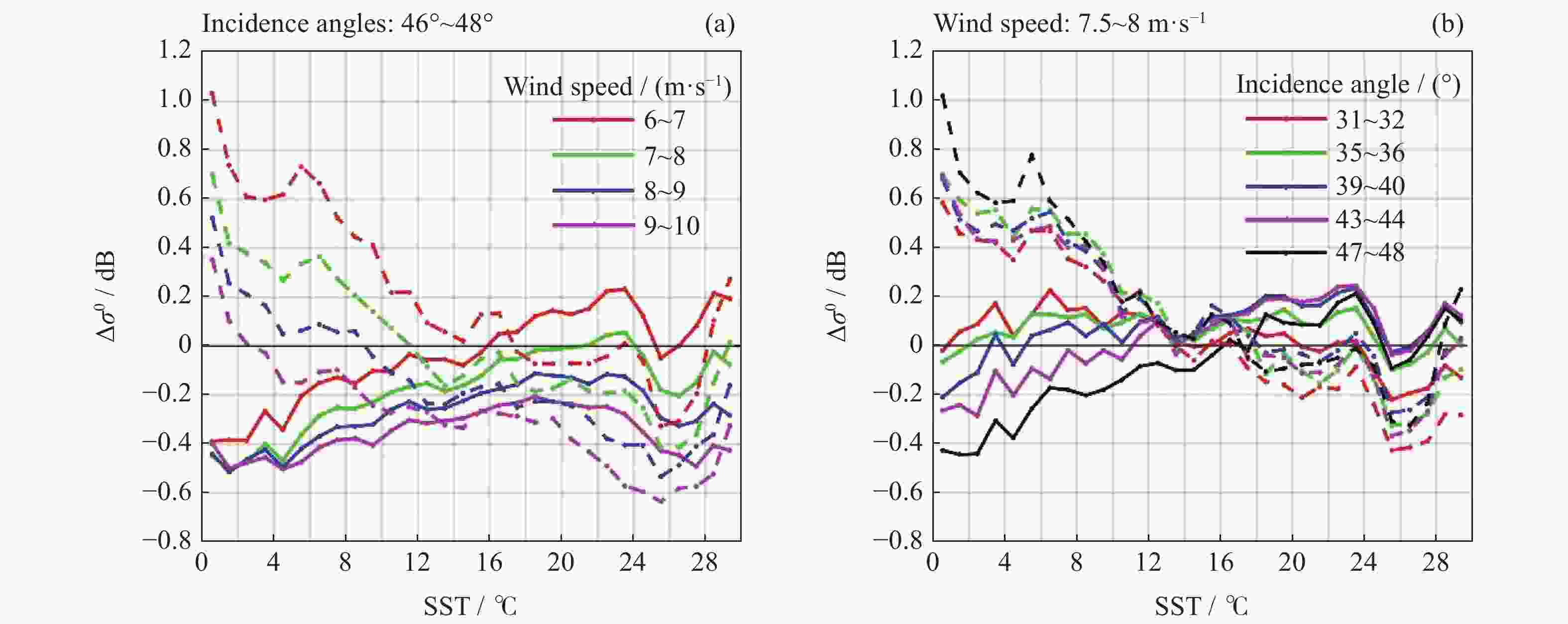
摘要: 卫星散射计通过测量海表粗糙度反演全球海面风场。对于Ku波段散射计，海表粗糙不仅和海面风场相关，还受海表温度的二阶效应调制。定量研究了海表温度对中法海洋卫星（CFOSAT）散射计（CSCAT）反演风速和后向散射测量的影响。结果表明，CSCAT两种极化方式测量的后向散射系数都会受到海表温度的影响，但是垂直极化中低入射角（θ < 36°）测量的后向散射系数几乎不随温度变化。因此CSCAT的风速偏差也随海表温度的变化而变化，且随着入射角的增大和风速的减小，海表温度对风速偏差的影响程度增大。在数据分析的基础上提出了一种考虑海表温度影响机制的地球物理模式函数，为未来CFOSAT散射计风场反演的海温校正提供参考。Abstract: Satellite scatterometer is designed to retrieve global sea surface winds by measuring the sea surface roughness. For Ku-band scatterometers, the sea surface roughness is not only affected by winds, but also by certain secondary effect, namely Sea Surface Temperature (SST). This paper presents a quantitative analysis of the SST effects on the China-France Oceanography Satellite (CFOSAT) scatterometer (CSCAT) backscatter measurements and wind retrievals. The results show that the backscatter coefficients measured by CSCAT vertically and horizontally polarized beams are both effected by SST, while for vertically polarized beams, the SST effect is nearly negligible at moderate and low incidence angles (θ < 36°). Consequently, the wind speed bias of CSCAT also changes along with SST, e.g., large SST-induced bias is associated with high incidence angles and/or low wind speed conditions. Finally, an SST-dependence Geophysical Model Function (GMF) is proposed, which opens a door for further improving the quality of CFOSAT scatterometer wind products.
-
图 1 在1°×1°全球网格中匹配数据集的年平均海表温度
Figure 1. Annual mean Sea Surface Temperature (SST) on a 1°×1°grid
图 2 CSCAT和 ASCAT与对应ECMWF风速的偏差（a）及风速概率密度函数（b）
Figure 2. Wind speed differences between CSCAT, ASCAT and ECMWF(a) and the wind speed Probability Density Function (PDF) (b)
图 3 在1°×1°全球网格上匹配数据集的平均风速偏差
Figure 3. Mean wind speed difference between CSCAT and ECMWF, the grid size is of 1°×1°
图 4
$ \Delta v_{{{{\rm{CE}}}}}' $ 随海表温度和平均风速的变化。黑实线代表每个风速区间的平均海表温度Figure 4.
$ \Delta v_{{{{\rm{CE}}}}}' $ as a function of Sea Surface Temperature (SST) and mean wind speed. Black line depicts the mean SST at each wind speed bin
图 6 平均
$ \Delta \sigma^{0} $ 随海表温度的变化。实线表示垂直极化，虚线表示水平极化Figure 6. Mean
$ \Delta \sigma^{0} $ as a function of Sea Surface Teamperature (SST). Solid lines indicate vertical-polarization, and the dashed lines indicate horizontal-polarization
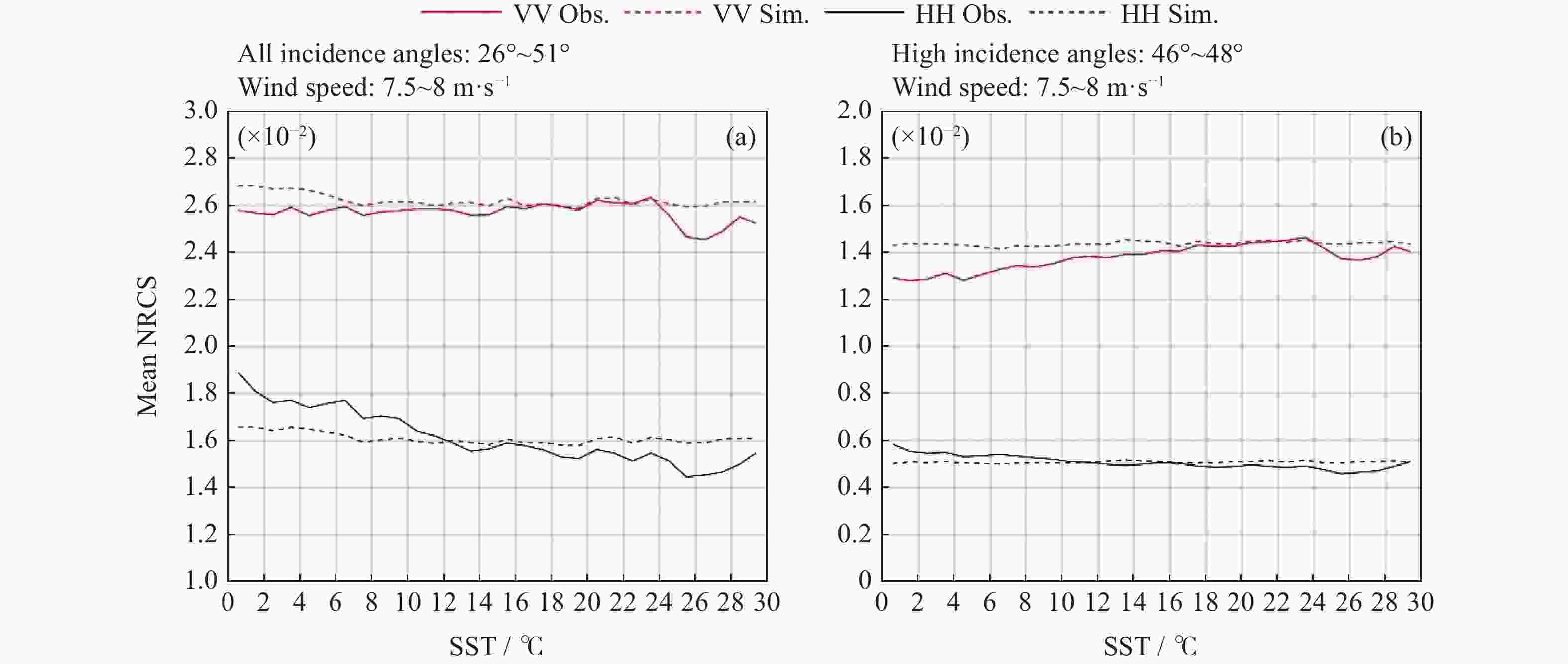
图 7
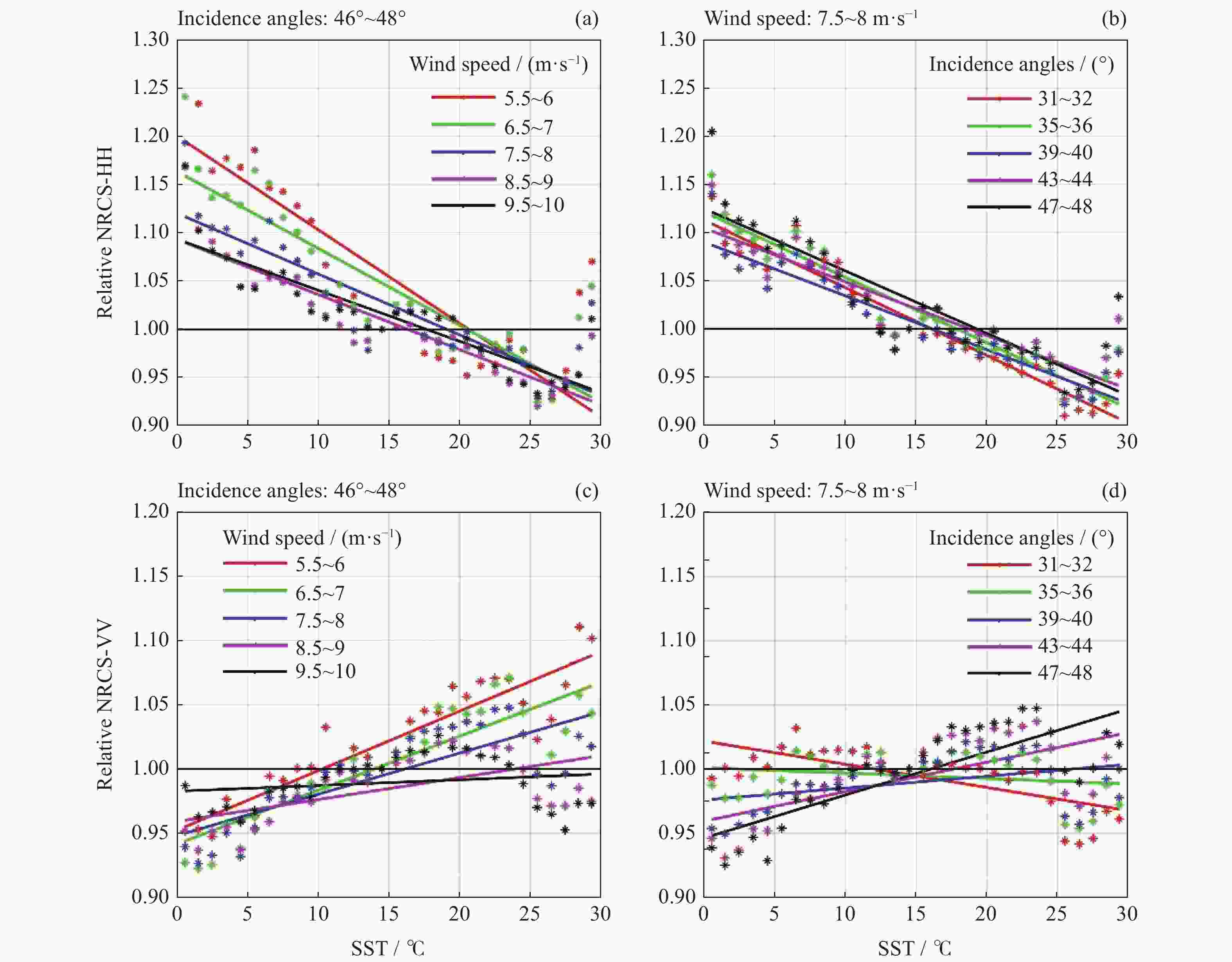
$ g{(v,t,\theta ,p)_{{{\rm{HH}}}}} $ 和$ g{(v,t,\theta ,p)_{{{\rm{VV}}}}} $ 在不同入射角和风速区间随海表温度的变化（星线表示探测结果，实线表示拟合后结果）Figure 7.
$ g{(v,t,\theta ,p)_{{{\rm{HH}}}}} $ and$ g{(v,t,\theta ,p)_{{{\rm{VV}}}}} $ as a function of Sea Surface Temperature (SST) in different incidence angle and wind speed ranges (The star line is measured result and the fitting result shown with the solid line) -
[1] STOFFELEN A, KUMAR R, ZOU J H, et al. Ocean surface vector wind observations[M]//BARALE V, GADE M. Remote Sensing of the Asian Seas. Cham: Springer, 2019: 429-447 [2] STOFFELEN A, VERSPEEK J A, VOGELZANG J, et al. The CMOD7 geophysical model function for ASCAT and ERS wind retrievals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 2123-2134 doi: 10.1109/JSTARS.2017.2681806 [3] WENTZ F J, SMITH D K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations[J]. Journal of Geophysical Research: Oceans, 1999, 104(C5): 11499-11514 doi: 10.1029/98JC02148 [4] LIU J Q, LIN W M, DONG X L, et al. First results from the rotating fan beam scatterometer onboard CFOSAT[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(12): 8793-8806 doi: 10.1109/TGRS.2020.2990708 [5] LIN W M, DONG X L, PORTABELLA M, et al. A perspective on the performance of the CFOSAT rotating fan-beam scatterometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 627-639 doi: 10.1109/TGRS.2018.2858852 [6] LIU W T. The effects of the variations in sea surface temperature and atmospheric stability in the estimation of average wind speed by SEASAT-SASS[J]. Journal of Physical Oceanography, 1984, 14(2): 392-401 doi: 10.1175/1520-0485(1984)014<0392:TEOTVI>2.0.CO;2 [7] GRODSKY S A, KUDRYAVTSEV V N, BENTAMY A, et al. Does direct impact of SST on short wind waves matter for scatterometry?[J]. Geophysical Research Letters, 2012, 39(12): L12602 [8] KUDRYAVTSEV V. On radar imaging of current features: 1. Model and comparison with observations[J]. Journal of Geophysical Research, 2005, 110(C7): C07016 [9] BENTAMY A, GRODSKY S A, CARTON J A, et al. Matching ASCAT and QuikSCAT winds[J]. Journal of Geophysical Research: Oceans, 2012, 117(C2): C02011 [10] WANG Z X, STOFFELEN A, ZHAO C F, et al. An SST-dependent Ku-band geophysical model function for RapidScat[J]. Journal of Geophysical Research: Oceans, 2017, 122(4): 3461-3480 doi: 10.1002/2016JC012619 [11] WANG Z X, STOFFELEN A, FOIS F, et al. SST dependence of Ku- and C-band backscatter measurements[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 2135-2146 doi: 10.1109/JSTARS.2016.2600749 [12] 陈克海, 解学通, 张金兰, 等. 一种温度相关的HY-2 A散射计地球物理模型函数[J]. 热带海洋学报, 2022, 41(2): 90-102 doi: 10.11978/2021038CHEN Kehai, XIE Xuetong, ZHANG Jinlan, et al. An SST dependent geophysical model function for HY-2 A scatterometer[J]. Journal of Tropical Oceanography, 2022, 41(2): 90-102 doi: 10.11978/2021038 [13] 解学通, 陈克海, 郭丽青, 等. 包含温度因子的海水地球物理模型函数建模研究[J]. 热带海洋学报, 2007, 26(6): 14-20 doi: 10.3969/j.issn.1009-5470.2007.06.003XIE Xuetong, CHEN Kehai, GUO Liqing, et al. Research on modeling of ocean water geophysical model function including ocean surface temperature[J]. Journal of Tropical Oceanography, 2007, 26(6): 14-20 doi: 10.3969/j.issn.1009-5470.2007.06.003 [14] SHARQAWY M H, LIENHARD V J H, ZUBAIR S M. Thermophysical properties of seawater: a review of existing correlations and data[J]. Desalination and Water Treatment, 2010, 16(1/2/3): 354-380 [15] NAYAR K G, PANCHANATHAN D, MCKINLEY G H, et al. Surface tension of seawater[J]. Journal of Physical and Chemical Reference Data, 2014, 43(4): 043103 doi: 10.1063/1.4899037 [16] KLEIN L, SWIFT C. An improved model for the dielectric constant of sea water at microwave frequencies[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(1): 104-111 doi: 10.1109/TAP.1977.1141539 [17] DE KLOE J, STOFFELEN A, VERHOEF A. Improved use of scatterometer measurements by using stress-equivalent reference winds[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 2340-2347 doi: 10.1109/JSTARS.2017.2685242 [18] DONLON C J, MARTIN M, STARK J, et al. The operational sea surface temperature and sea ice analysis (OSTIA) system[J]. Remote Sensing of Environment, 2012, 116: 140-158 doi: 10.1016/j.rse.2010.10.017 [19] WANG Z X, ZOU J H, STOFFELEN A, et al. Scatterometer sea surface wind product validation for HY-2 C[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 6156-6164 doi: 10.1109/JSTARS.2021.3087742 [20] LIN W M, PORTABELLA M, STOFFELEN A, et al. ASCAT wind quality under high subcell wind variability conditions[J]. Journal of Geophysical Research: Oceans, 2015, 120(8): 5804-5819 doi: 10.1002/2015JC010861 [21] LIN W M, PORTABELLA M. Toward an improved wind quality control for RapidScat[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3922-3930 doi: 10.1109/TGRS.2017.2683720 [22] STILES B W, YUEH S H. Impact of rain on spaceborne Ku-band wind scatterometer data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1973-1983 doi: 10.1109/TGRS.2002.803846 [23] PORTABELLA M. Wind Field Retrieval from Satellite Radar Systems[D]. Barcelona: University of Barcelona, 2002 -
下载:
点击查看大图
计量
- 文章访问数: 44
- HTML全文浏览量: 10
- PDF下载量: 11
- 被引次数: 0
