黏弹性双自由面热毛细液层的不稳定性
doi: 10.11728/cjss2023.04.2023.04.yg07 cstr: 32142.14.cjss2023.04.2023.04.yg07
Instability of Viscoelastic Thermocapillary Liquid Layers with Two Free Surfaces
-
摘要: 在微重力条件下，双自由面液层是实现新型材料晶体生长的一种潜在方式，对其流动进行稳定性分析对于薄膜结晶等应用具有重要意义。本文采用线性稳定性理论研究了黏弹性双自由面热毛细液层的不稳定性。在不同Prandtl数(Pr)下得到临界Marangoni数(Mac)与弹性数(ε)的函数关系，并分析了临界模态的流场和能量机制。研究发现流场存在三种临界模态，分别是斜波、流向波和展向稳态，且三者均受弹性影响。小和高Pr的临界模态为斜波和流向波。在中等Pr下，随着ε的增加，临界模态由斜波变为流向波，最终变为展向稳态模态。在小Pr下，热点会随着ε的增大从液体层表面移动到内部。本研究还考查了溶剂黏度与总黏度比($\zeta $)对不稳定机制和临界模态的影响。在高Pr下，增加$\zeta $可以提高液体层的稳定性。然而在中小Pr下，增大$\zeta $会导致弱弹性处的流动变得不稳定。能量分析表明：在小Pr下，弱弹性处的扰动应力做功耗散能量，而在强弹性处则会提供能量。在中高Pr下，扰动动能的主要能量来源是表面张力做功，基本流做功可以忽略不计。将双自由面液层与单自由面液层进行对比发现，在Ma较小时，双自由面液层的弹性不稳定性更加明显。Abstract: In microgravity environments, dual-free surface liquid layer is a promising method for growing new material crystals, stability analysis of its flow is of great significance for applications such as thin film crystallization. The instability of viscoelastic thermocapillary liquid layers with two free surfaces is examined by linear stability analysis. The critical Marangoni number (Mac) is determined as a function of the elastic number (ε) and the Prandtl number (Pr). The flow fields and energy mechanisms of preferred modes are analyzed. Three kinds of instabilities are found: oblique wave, streamwise wave and spanwise stationary mode, whose properties are all significantly affected by the elasticity. The preferred modes are the oblique wave and streamwise wave at small and large Pr. When Pr = 1, the preferred mode changes from the oblique wave to the streamwise wave, and finally the spanwise stationary mode with the increase of ε. At small Pr, the hot spots move from the surface to the interior of the liquid layer with the increase of ε. The effect of the ratio ($\zeta $) of solvent viscosity to the total viscosity on the instability mechanism and the preferred modes are demonstrated. When Pr is large, the increase of $\zeta $ often makes the flow more stable. However, for small and moderate Pr, the flow is destabilized by the increase of $\zeta $ at weak ε. Energy analysis shows that at the small Pr, the perturbation stress at the weak ε dissipates energy while it provides energy at the strong ε. At the moderate and large Pr, the primary source of energy for perturbation energy is the work done by surface tension, and the contribution of the base flow can be neglected. Comparing the double free surface liquid layer with the single free surface liquid layer, it is found that the elastic instability of the double free surface liquid layer is more prominent when the Ma number is small.
-
Key words:
- Thermocapillary /
- Viscoelasticity /
- Instability
-
图 1 黏弹性双自由面热毛细液层
Figure 1. Viscoelastic thermocapillary liquid layer with two free surfaces
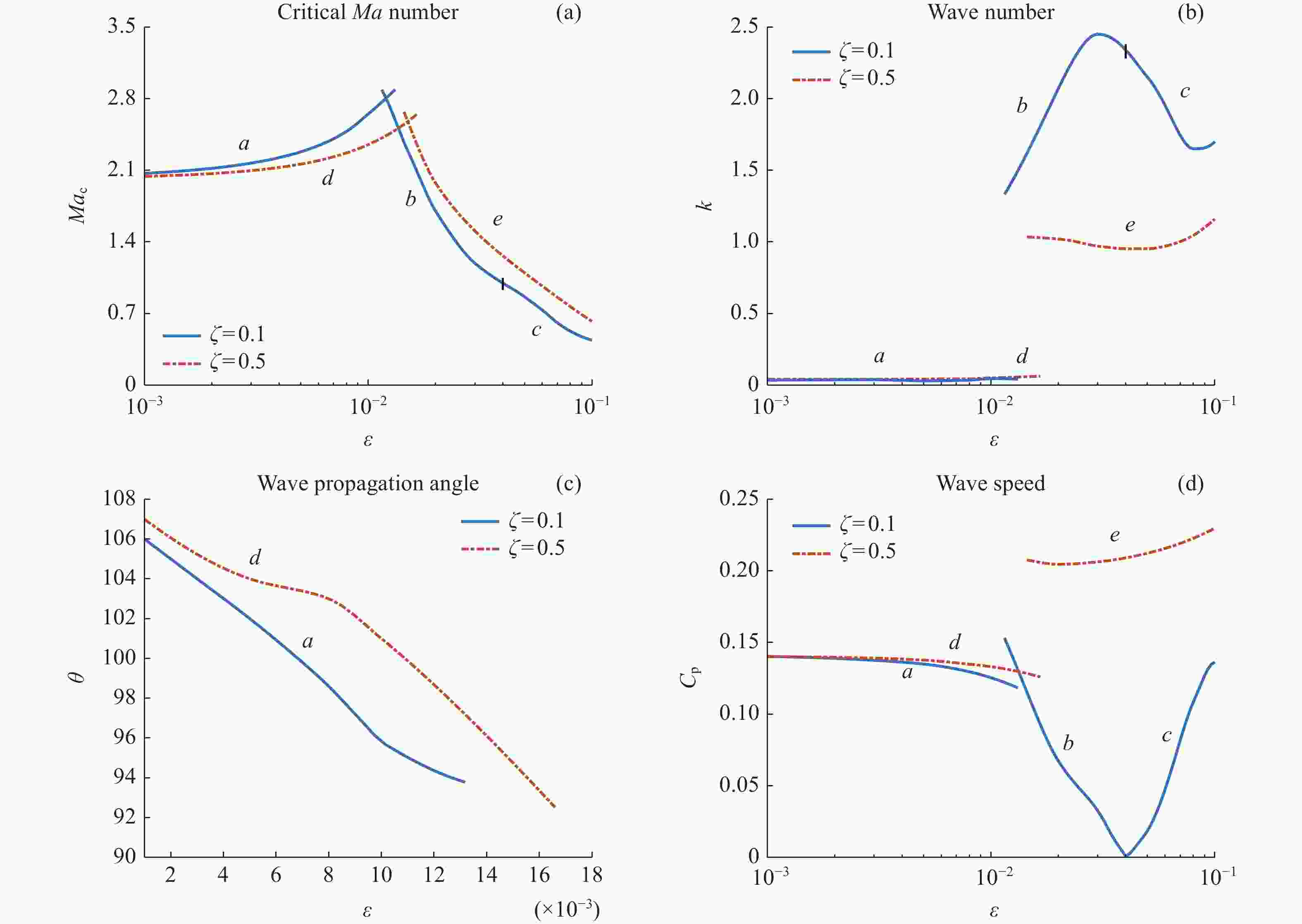
图 2 Pr = 0.01时Mac 随ε 的变化曲线及相应的波数、波传播角和波速。曲线a和d对应逆向斜波，b和e对应同向流向波，c为逆向流向波
Figure 2. Variation of Mac with ε at Pr = 0.01 and the wave number, wave propagation angle and wave speed corresponding to critical Ma number. Curves a, d correspond to upstream oblique wave; b, e correspond to downstream streamwise wave; and c corresponds to upstream streamwise wave
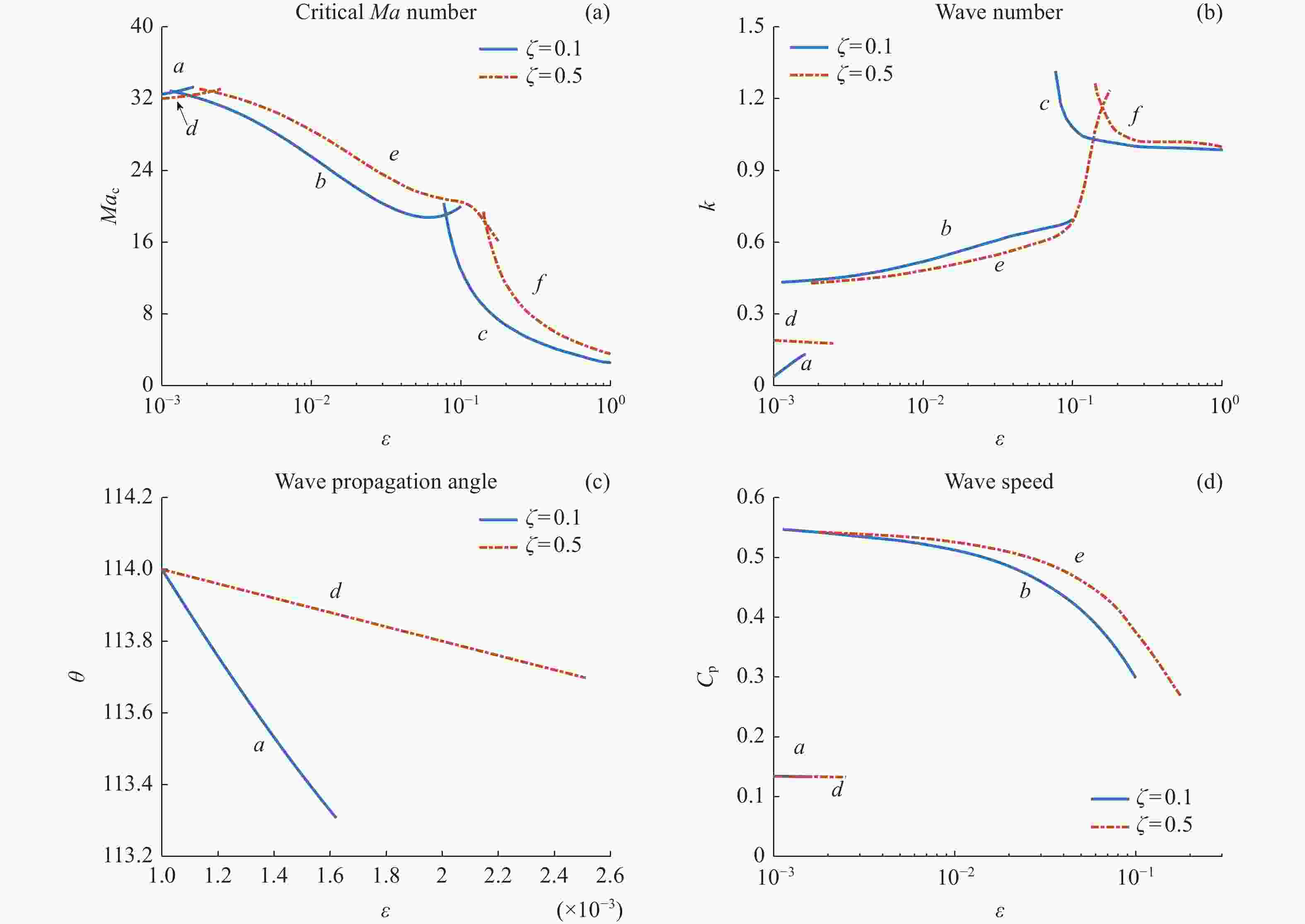
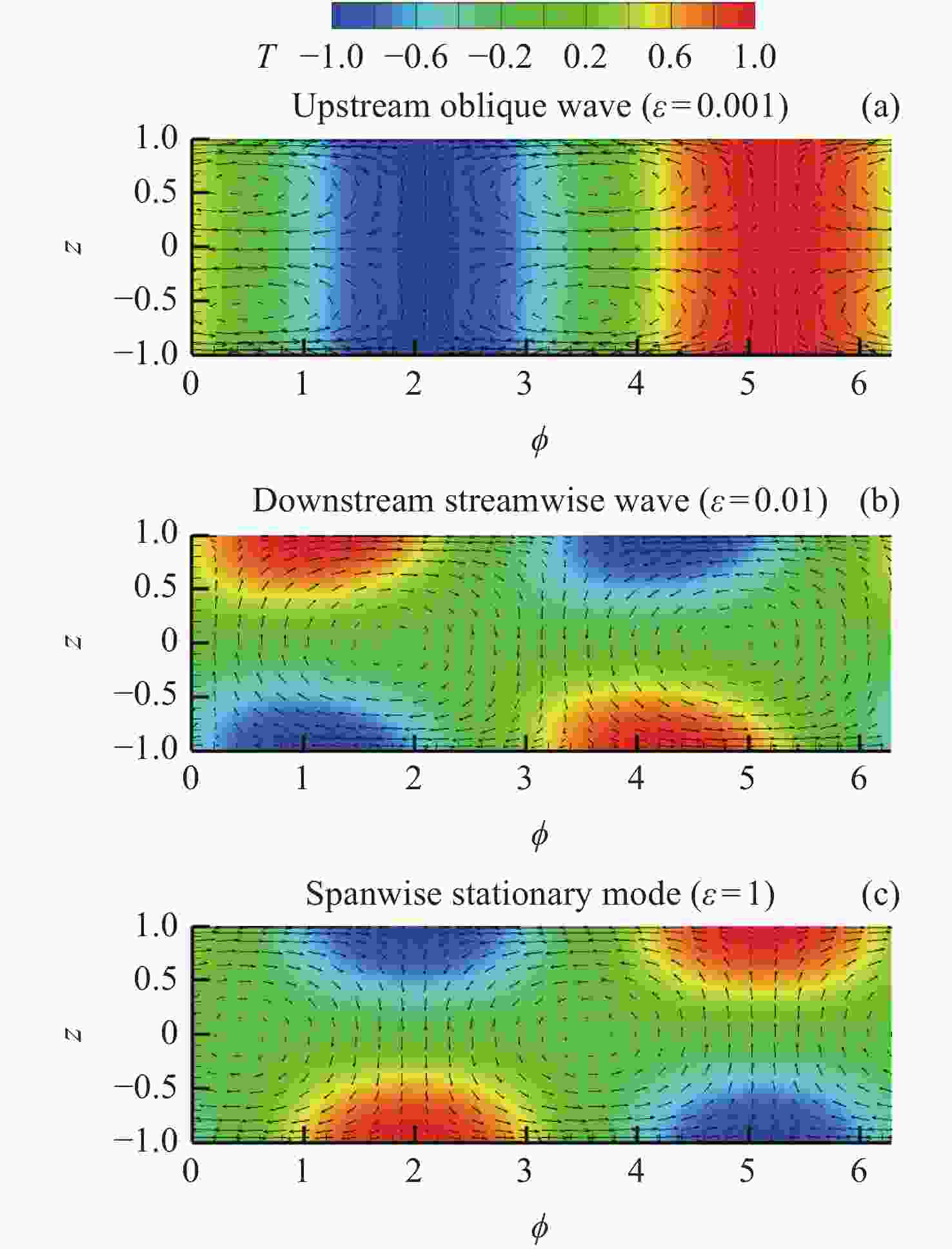
图 3 Pr = 1时Mac 随ε 的变化曲线及相应的波数、波传播角和波速。a和d曲线对应逆向斜波，b和e对应同向流向波，c和f对应展向稳态模态
Figure 3. Variation of Mac with ε at Pr = 1 and the wave number, wave propagation angle and wave speed corresponding to critical Ma number. Curves a, d correspond to upstream oblique wave; b, e correspond to downstream streamwise wave; and c, f correspond to spanwise stationary mode
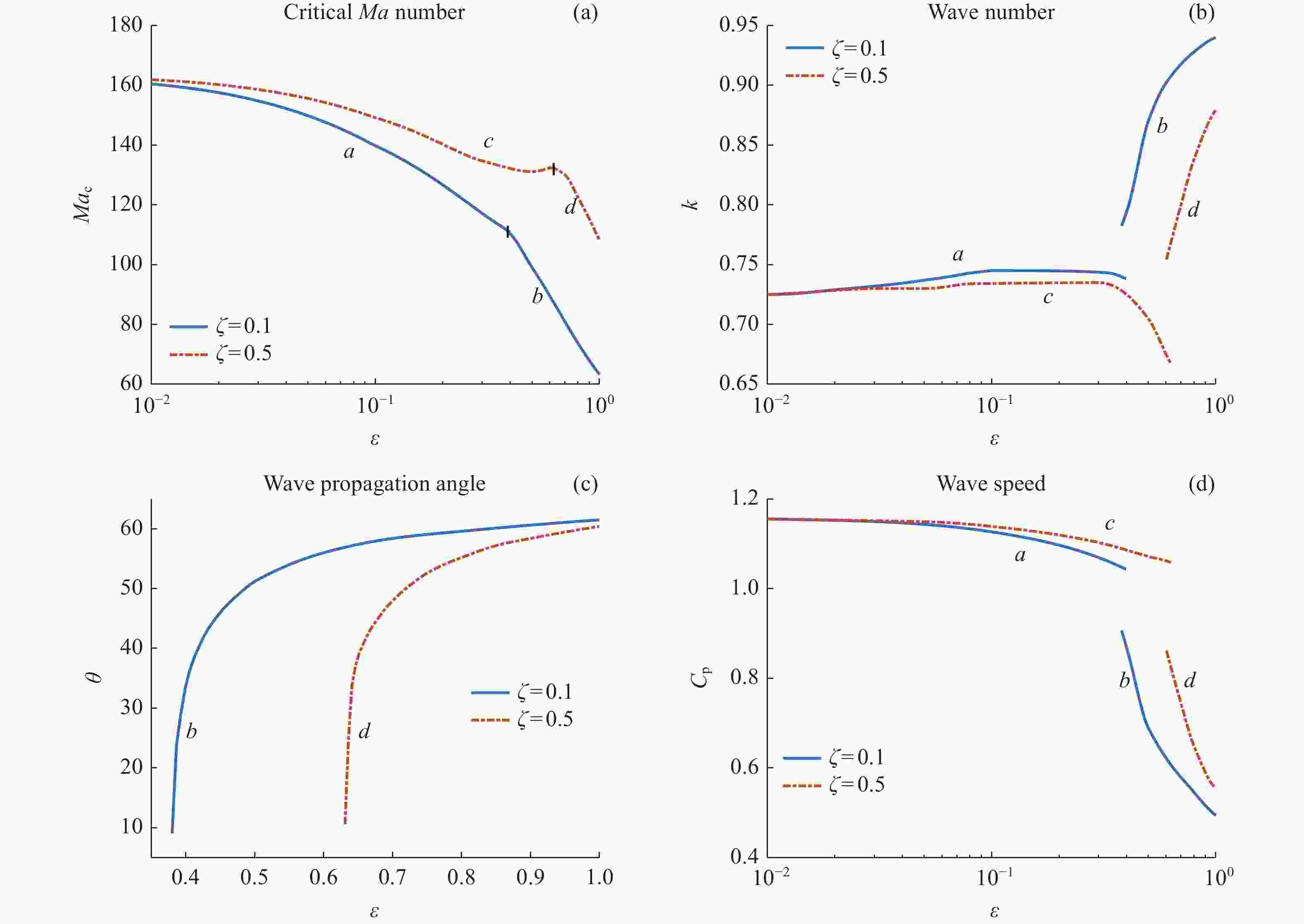
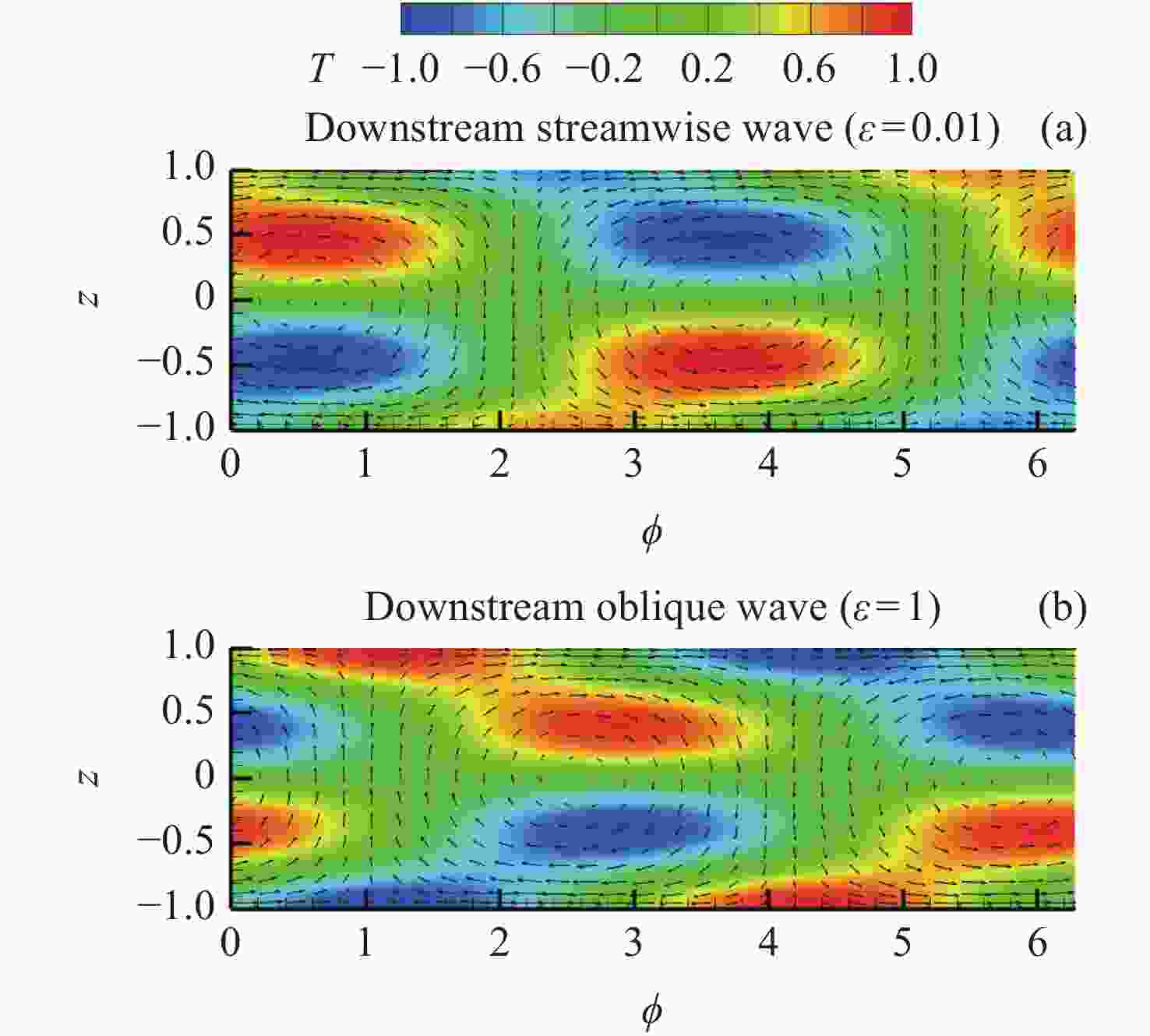
图 4 Pr = 100时Mac随ε 的变化曲线及相应的波数、波传播角和波速。曲线a和c对应同向流向波，b和d对应同向斜波
Figure 4. Variation of Mac with ε at Pr = 100 and the wave number, wave propagation angle and wave speed corresponding to critical Ma number. Curves a, c correspond to downstream streamwise wave, and b, d correspond to downstream oblique wave
图 5 Pr = 0.01时不同临界模态对应的扰动流场
Figure 5. Perturbation flow field of the different preferred modes at Pr = 0.01
图 6 Pr = 1时不同临界模态对应的扰动流场
Figure 6. Perturbation flow field of the different preferred modes at Pr = 1
图 7 Pr = 100时不同临界模态对应的扰动流场
Figure 7. Perturbation flow field of the different preferred modes at Pr = 100
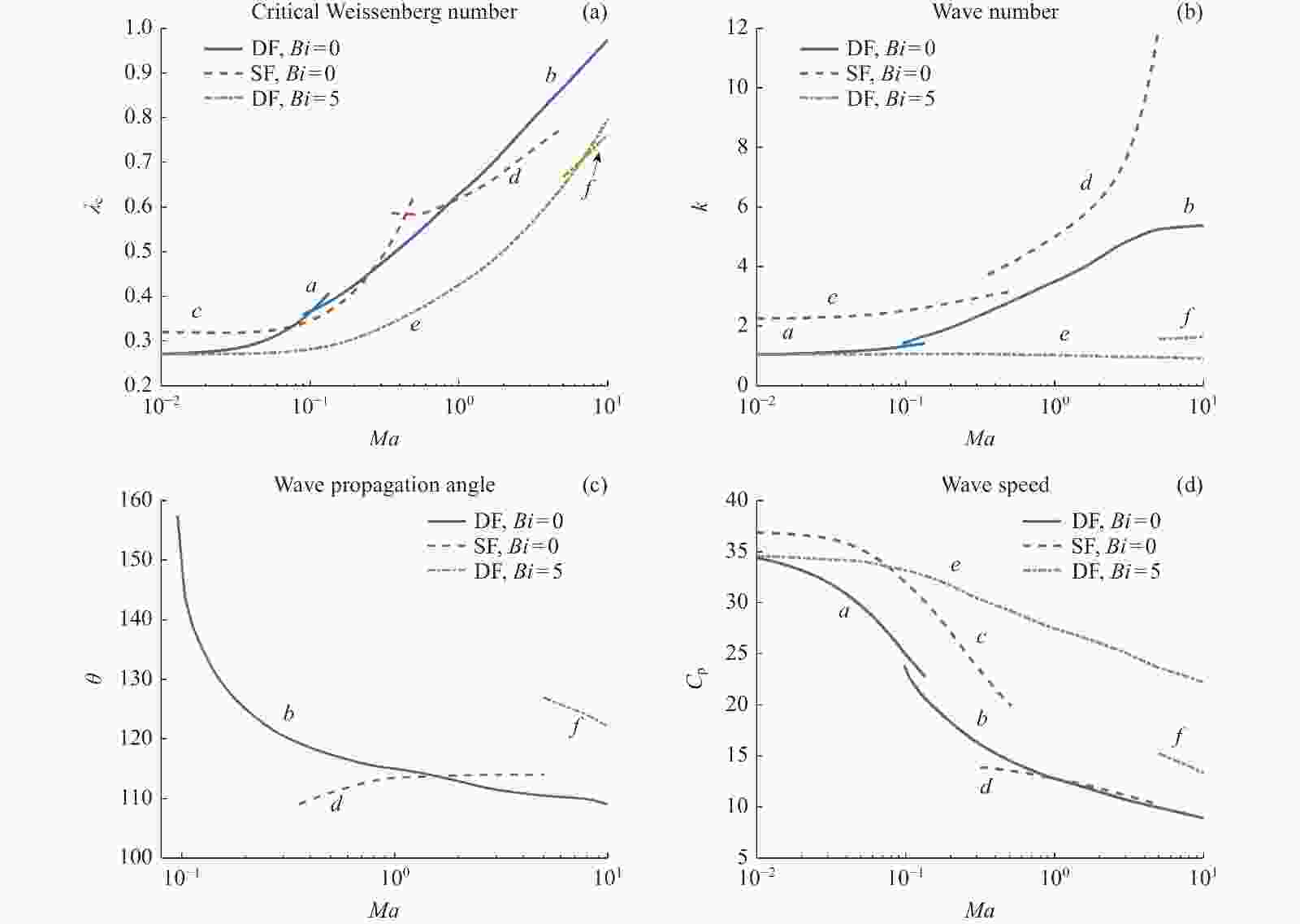
图 8 单自由液层(SF)与双自由面液层(DF)在不同Bi下λc随Ma的变化曲线及相应的波数、波传播角和波速。曲线a, c, e对应逆向流向波；b, d, f 对应逆向斜波
Figure 8. Variation of λc with Ma in SF and DF under different Bi and the wave number, wave propagation angle and wave speed corresponding to critical Weissenberg number. Curves a, c, e correspond to upstream streamwise wave, and b, d, f correspond to upstream oblique wave
表 1 Pr = 1，Ma = 30.9，k = 0.074，θ = 65.9°时牛顿流体与Oldroyd-B流体最不稳定特征值的比较
Table 1. Comparison of most unstable eigenvalues for Newtonian fluid and Oldroyd-B fluid at Pr = 1, Ma = 30.9, k = 0.074, θ = 65.9°
牛顿流体
(η = λ = 0)Oldroyd-B流体
(ε = 0.01, $\zeta \to 1$)0.00000094 +0.010057 i 0.00000094 +0.010057 i –0.00059576 –0.010066 i –0.00059576 –0.010066 i –0.04806797 –0.050246 i –0.04806797 –0.050246 i –0.07455415 +0.022369 i –0.07455415 +0.022369 i 
下载: 导出CSV
表 2 不同Pr数下各扰动能量变化项的值
Table 2. Values of perturbation energy variation terms at different Pr
Pr $\varepsilon $ $ - N$ $M$ $I$ 0.01 0.001 –0.036660 0.036618 0.000046 0.01 –0.032730 0.032651 0.000086 0.05 0.026172 –0.000891 –0.025284 0.1 0.047090 0.000690 –0.047711 1 0.001 –0.233990 0.233960 0.000031 0.01 –0.164285 0.176779 –0.012495 0.1 –0.176756 0.237478 –0.060724 1 –0.169524 0.220168 –0.050648 100 0.001 –2.441530 2.448137 –0.006613 0.01 –2.493753 2.500407 –0.006645 0.1 –2.849847 2.855890 –0.006042 1 –5.594289 5.650019 –0.055716
下载: 导出CSV
-
[1] LIU Y, ZENG Z, ZHANG L Q, et al. Effect of crystal rotation on the instability of thermocapillary-buoyancy convection in a Czochralski model[J]. Physics of Fluids, 2021, 33(10): 104101 doi: 10.1063/5.0062615 [2] BÉG O A, VENKATADRI K, PRASAD V R, et al. Numerical simulation of hydromagnetic Marangoni convection flow in a Darcian porous semiconductor melt enclosure with buoyancy and heat generation effects[J]. Materials Science and Engineering:B, 2020, 261: 114722 doi: 10.1016/j.mseb.2020.114722 [3] BASARAN O A, GAO H J, BHAT P P. Nonstandard inkjets[J]. Annual Review of Fluid Mechanics, 2013, 45: 85-113 doi: 10.1146/annurev-fluid-120710-101148 [4] CHEN L, JIN G H, DAI Q W, et al. Droplets impacting and migrating on structured surfaces with imposed thermal gradients[J]. Journal of Tribology, 2022, 144(4): 041807 doi: 10.1115/1.4052779 [5] WANG T S, SHI W Y, DUAN F. Marangoni convection instabilities in an evaporating droplet on a non-isothermal substrate[J]. International Journal of Heat and Mass Transfer, 2022, 195: 123140 doi: 10.1016/j.ijheatmasstransfer.2022.123140 [6] HU K X, ZHANG S N, CHEN Q S. Surface wave instability in the thermocapillary migration of a flat droplet[J]. Journal of Fluid Mechanics, 2023, 958: A22 doi: 10.1017/jfm.2023.77 [7] KARBALAEI A, KUMAR R, CHO H J. Thermocapillarity in microfluidics—a review[J]. Micromachines, 2016, 7(1): 13 doi: 10.3390/mi7010013 [8] KOWAL K N, DAVIS S H, VOORHEES P W. Thermocapillary instabilities in a horizontal liquid layer under partial basal slip[J]. Journal of Fluid Mechanics, 2018, 855: 839-859 doi: 10.1017/jfm.2018.684 [9] SMITH M K, DAVIS S H. Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities[J]. Journal of Fluid Mechanics, 1983, 132: 119-144 doi: 10.1017/S0022112083001512 [10] BACH C, SCHWABE D. Surface waves in thermocapillary flow-revisited[J]. The European Physical Journal Special Topics, 2015, 224(2): 319-340 doi: 10.1140/epjst/e2015-02363-5 [11] LI Y R, IMAISHI N, AZAMI T, et al. Three-dimensional oscillatory flow in a thin annular pool of silicon melt[J]. Journal of Crystal Growth, 2004, 260(1/2): 28-42 [12] PATNE R, AGNON Y, ORON A. Thermocapillary instabilities in a liquid layer subjected to an oblique temperature gradient[J]. Journal of Fluid Mechanics, 2021, 906: A12 doi: 10.1017/jfm.2020.747 [13] CHEN E H, XU F. Transient Marangoni convection induced by an isothermal sidewall of a rectangular liquid pool[J]. Journal of Fluid Mechanics, 2021, 928: A6 doi: 10.1017/jfm.2021.795 [14] HU K X, HE M, CHEN Q S, et al. Effect of gravity on the stability of viscoelastic thermocapillary liquid layers[J]. International Journal of Heat and Mass Transfer, 2018, 123: 776-786 doi: 10.1016/j.ijheatmasstransfer.2018.02.088 [15] BAIOUMY B, CHEBBI R, JABBAR N A. Bingham fluid flow in the entrance region of a pipe[J]. Journal of Fluids Engineering, 2021, 143(2): 024503 doi: 10.1115/1.4048610 [16] BOARO A, LAPPA M. On the competition of transverse and longitudinal modes of Marangoni convection in a three-dimensional layer of viscoelastic fluid[J]. Physics of Fluids, 2022, 34(12): 123103 doi: 10.1063/5.0131461 [17] 王胜, 胡开鑫. Bingham流体双自由面热毛细液层的稳定性分析[J]. 力学学报, 2022, 54(12): 3398-3407 doi: 10.6052/0459-1879-22-364WANG Sheng, HU Kaixin. Stability analysis of thermocapillary liquid layers with two free surfaces for a Bingham fluid[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(12): 3398-3407 doi: 10.6052/0459-1879-22-364 [18] YAN C Y, HU K X, CHEN Q S. Thermocapillary instabilities of liquid layers on an inclined plane[J]. Physics of Fluids, 2018, 30(8): 082101 doi: 10.1063/1.5039149 [19] HU K X, ZHENG S, CHEN Q S. Transient growth in thermocapillary liquid layers[J]. Physical Review Fluids, 2020, 5(1): 014001 doi: 10.1103/PhysRevFluids.5.014001 [20] 赵诚卓, 胡开鑫. 双自由面溶质-热毛细液层的不稳定性[J]. 力学学报, 2022, 54(2): 291-300 doi: 10.6052/0459-1879-21-148ZHAO Chengzhuo, HU Kaixin. Instability in the solutal-thermocapillary liquid layer with two free surface[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(2): 291-300 doi: 10.6052/0459-1879-21-148 [21] PETTIT D. Saturday morning science videos[EB/OL]. (2003). https://blog.sciencenet.cn/blog-420554-701386.html [22] WATANABE T, KOWATA Y, UENO I. Flow transition and hydrothermal wave instability of thermocapillary-driven flow in a free rectangular liquid film[J]. International Journal of Heat and Mass Transfer, 2018, 116: 635-641 doi: 10.1016/j.ijheatmasstransfer.2017.09.059 [23] UENO I, TORII T. Thermocapillary-driven flow in a thin liquid film sustained in a rectangular hole with temperature gradient[J]. Acta Astronautica, 2010, 66(7/8): 1017-1021 [24] MESSMER B, LEMEE T, IKEBUKURO K, et al. Confined thermo-capillary flows in a double free-surface film with small Marangoni Numbers[J]. International Journal of Heat and Mass Transfer, 2014, 78: 1060-1067 doi: 10.1016/j.ijheatmasstransfer.2014.06.053 [25] YAMAMOTO T, TAKAGI Y, OKANO Y, et al. Numerical investigation of oscillatory thermocapillary flows under zero gravity in a circular liquid film with concave free surfaces[J]. Physics of Fluids, 2016, 28(3): 032106 doi: 10.1063/1.4943246 [26] HU K X, ZHAO C Z, ZHANG S N, et al. Instabilities of thermocapillary liquid layers with two free surfaces[J]. International Journal of Heat and Mass Transfer, 2021, 173: 121217 doi: 10.1016/j.ijheatmasstransfer.2021.121217 [27] SOLEYMANIHA M, FELTS J R. Design of a heated micro-cantilever optimized for thermo-capillary driven printing of molten polymer nanostructures[J]. International Journal of Heat and Mass Transfer, 2016, 101: 166-174 doi: 10.1016/j.ijheatmasstransfer.2016.04.063 [28] HU K X, LIU R, HE M, et al. Elastic instability in the thermocapillary convection at low Reynolds numbers[J]. Journal of Non-Newtonian Fluid Mechanics, 2017, 250: 43-51 doi: 10.1016/j.jnnfm.2017.10.009 [29] SARMA R, MONDAL P K. Thermosolutal Marangoni instability in a viscoelastic liquid film: effect of heating from the free surface[J]. Journal of Fluid Mechanics, 2021, 909: A12 doi: 10.1017/jfm.2020.880 [30] DÁVALOS-OROZCO L A, CHÁVEZ A E. Thermocapillary convection in a viscoelastic fluid layer under a horizontal temperature gradient[J]. Journal of Applied Polymer Science, 1991, 49: 141-153 doi: 10.1002/app.1991.070490014 [31] HU K X, HE M, CHEN Q S. Instability of thermocapillary liquid layers for Oldroyd-B fluid[J]. Physics of Fluids, 2016, 28(3): 033105 doi: 10.1063/1.4943971 [32] PATNE R, AGNON Y, ORON A. Thermocapillary instability in a viscoelastic liquid layer under an imposed oblique temperature gradient[J]. Physics of Fluids, 2021, 33(1): 012107 doi: 10.1063/5.0036202 [33] RAJAGOPAL K R, BHATNAGAR R K. Exact solutions for some simple flows of an Oldroyd-B fluid[J]. Acta Mechanica, 1995, 113(1/2/3/4): 233-239 [34] TEITEL M, SCHWABE D, GELFGAT A Y. Experimental and computational study of flow instabilities in a model of Czochralski growth[J]. Journal of Crystal Growth, 2008, 310(7/8/9): 1343-1348 [35] TOUSSAINT G, BODIGUEL H, DOUMENC F, et al. Experimental characterization of buoyancy-and surface tension-driven convection during the drying of a polymer solution[J]. International Journal of Heat and Mass Transfer, 2008, 51(17/18): 4228-4237 [36] 章绍能, 胡开鑫. 黏弹性液滴热毛细迁移的对流不稳定[J]. 力学学报, 2021, 53(5): 1313-1323 doi: 10.6052/0459-1879-20-443ZHANG Shaoneng, HU Kaixin. Convective instability in thermocapillary migration of a viscoelastic droplet[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1313-1323 doi: 10.6052/0459-1879-20-443 -
-
下载:
计量
- 文章访问数: 276
- HTML全文浏览量: 87
- PDF下载量: 44
-
被引次数:
0(来源:Crossref)
0(来源:其他)
