共线平动点中心流形上的轨道转移问题
doi: 10.11728/cjss2024.03.2023-0098 cstr: 32142.14.cjss2024.03.2023-0098
-
杨富涛 男, 1999年11月出生于四川省宜宾市, 毕业于南京航空航天大学航天学院, 硕士研究生, 主要从事深空探测轨道动力学以及飞行器控制等方面的研究. E-mail: tt18284863524@163.com -
张汉清 男, 1980年11月出生于河南省开封市, 现为南京航空航天大学航天学院讲师, 硕士生导师, 主要从事深空探测轨道动力学等方面的研究. 本文通信作者. E-mail: hanqing@nuaa.edu.cn
作者简介:
Orbital Transfer Problem on the Central Manifold of Libration Points
-
摘要: 圆形限制性三体问题共线平动点附近的平动点轨道由于其独特的动力学特性, 在深空探测任务中有着重要价值, 这些轨道间的轨道转移问题值得进行系统性研究. 针对平动点轨道的计算与延拓, 提出了一种基于数值的系统性计算平动点轨道的方法以及状态伴随法的轨道稳定维持策略. 在此基础上, 通过对大量平动点轨道不变流形以及平动点相空间中心流形的研究, 设计了一套通过脉冲机动实现平动点轨道间轨道转移的系统性解决方案. 该方法充分利用平动点动力学特性, 在仿真验证中证实了方案的有效性, 为平动点轨道转移研究提供了新的思路.Abstract: The Circular Restricted Three-body Problem (CR3BP) exhibits highly complex nonlinear dynamical characteristics in the vicinity of its libration points. The various periodic and quasi-periodic orbits within this region hold significant value for increasingly complex deep space exploration missions, offering more possibilities and flexibility in the design and control of mission trajectories. The issue of orbit transfers between these libration points warrants systematic investigation. To compute orbits around libration points, a numerical computation method based on escape time is proposed, enabling the unified calculation of various quasi-periodic orbits across a broad range of energy levels. Based on the manifold configuration of libration point orbit state points, a universal orbit maintenance strategy called state-adjoint techniques is proposed, yielding schemes that can sustain long-term stable operation of various libration point orbits. Building on extensive studies of invariant manifolds and Poincaré sections associated with numerous libration point orbits, a comprehensive solution has been designed to enable orbit transfers between libration points through pulse maneuvers. This method fully leverages the dynamical features of libration points and has been proven effective through simulation validation, offering new insights for research on libration point orbit transfers.
-
图 2 稳定流形(实线)与不稳定流形(虚线)曲线
Figure 2. Stable (solid line) and unstable (dotted line) manifold plots
图 4 选取数据点稳定流形(实线)与不稳定流形(虚线)参数
Figure 4. Diagram of stable manifold (solid line) and unstable manifold (dotted line) parameters
图 6 空间中对称点稳定流形(实线)与不稳定流形(虚线)参数
Figure 6. Stable (solid line) and unstable manifold (dotted line) parameters at symmetrical points in space
图 17 地月系统L2点南北晕轨道转移
Figure 17. Orbital transfer between the north-halo and south-halo orbits at L2 points of the Earth-Moon system
图 18 地月系统L1点同族晕轨道转移
Figure 18. Orbital transfer between the halo orbital family at L1 points of the Earth-Moon system
表 1 平动点轨道初始状态与校正k值
Table 1. Initial state of the translational point track with corrected k-value
初始状态 (x0, y0, z0, α, β)=(0.84, 0.02, 0, 2.92, 1.17)
δ=0.00005校正次数 k 校正次数 k 1 –1.017×10–10 8 –4.62×10–11 2 –3.447×10–9 9 1.142×10–7 3 1.783×10–7 10 –2.903×10–6 4 –4.545×10–9 11 3.615×10–11 5 2.158×10–7 12 –8.679×10–8 6 4.728×10–8 13 2.455×10–6 7 –1.281×10–6 14 1.988×10–8 
下载: 导出CSV
表 2 南北晕轨道转移参数
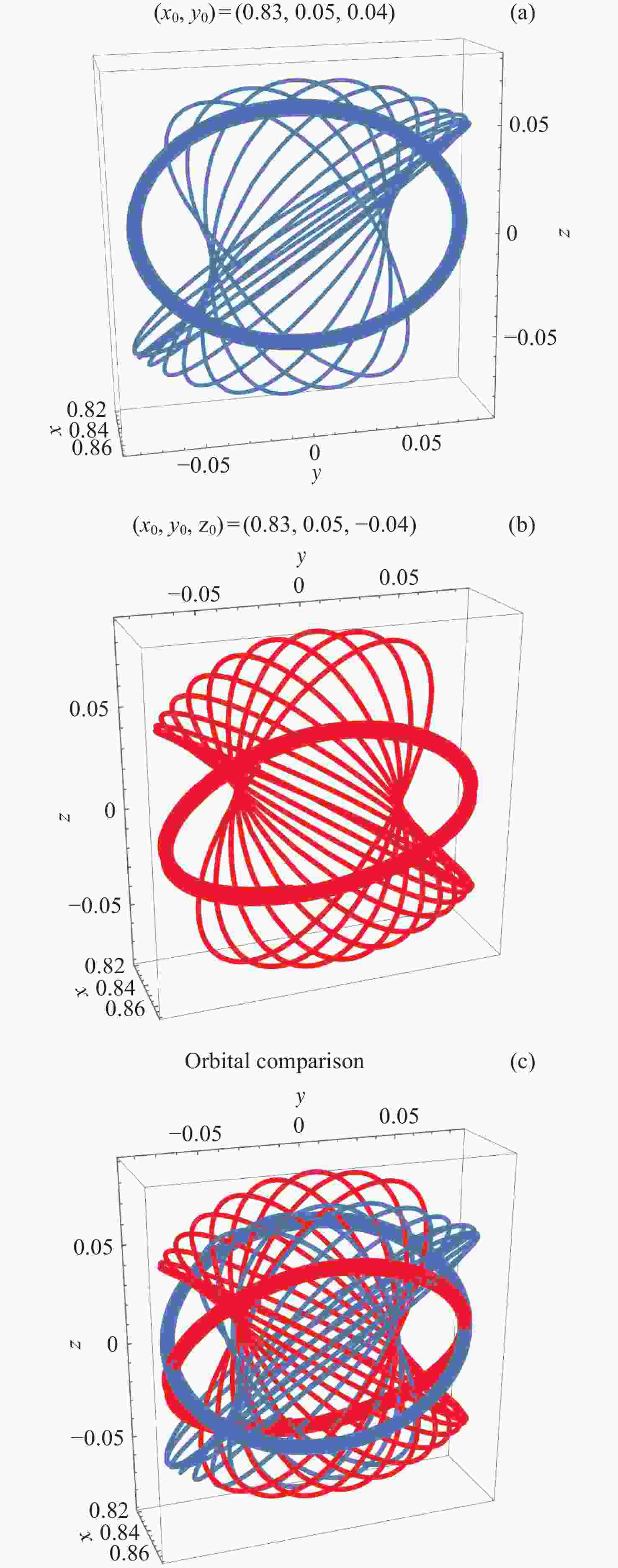
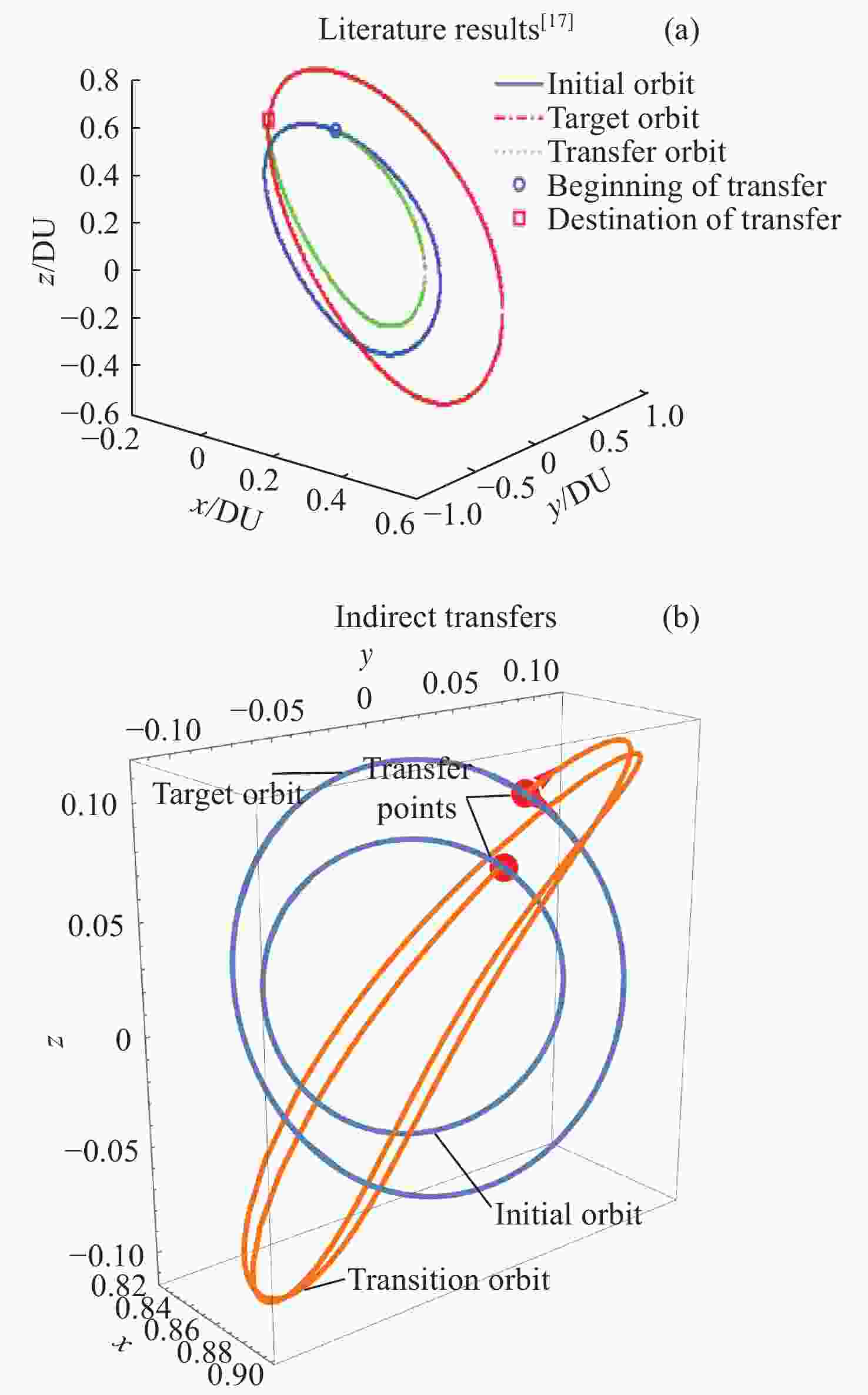
Table 2. Orbital transfer parameter between the north-halo and south-halo orbits
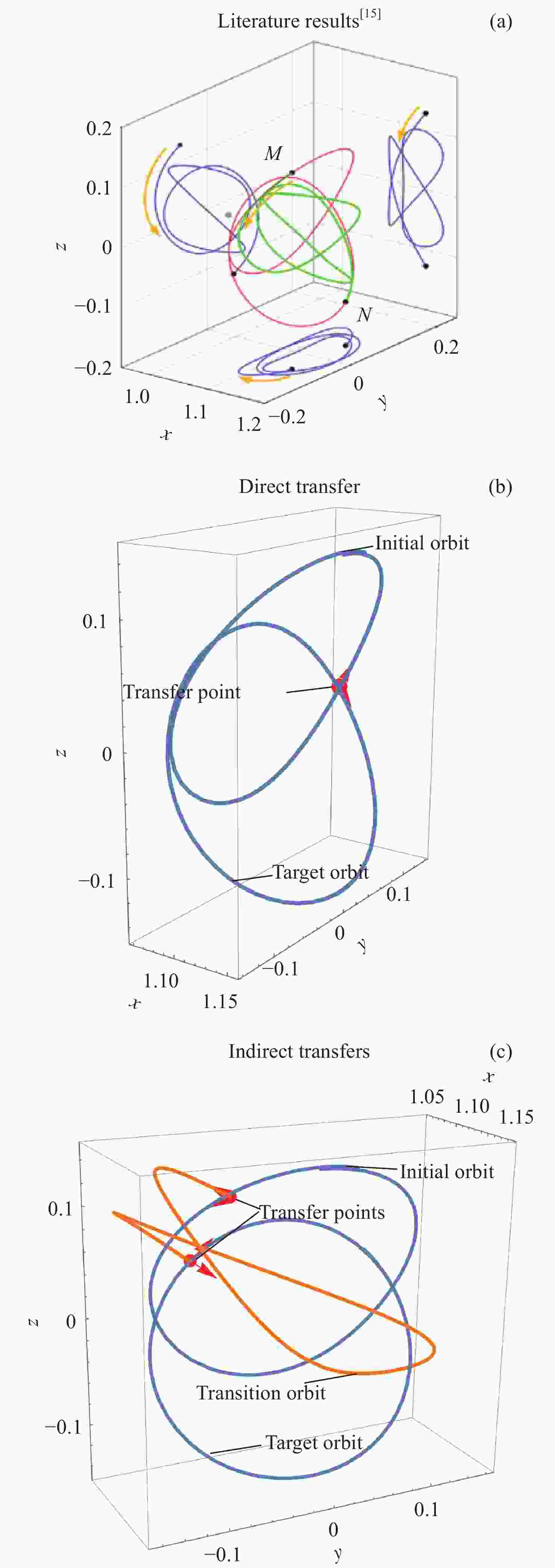
转移参数 转移时间/d 总Δv /(m⋅s–1) 文献数据 39.06 488.342 直接转移 0 427.325 间接转移 20.87 569.808
下载: 导出CSV
表 3 同族晕轨道间转移参数
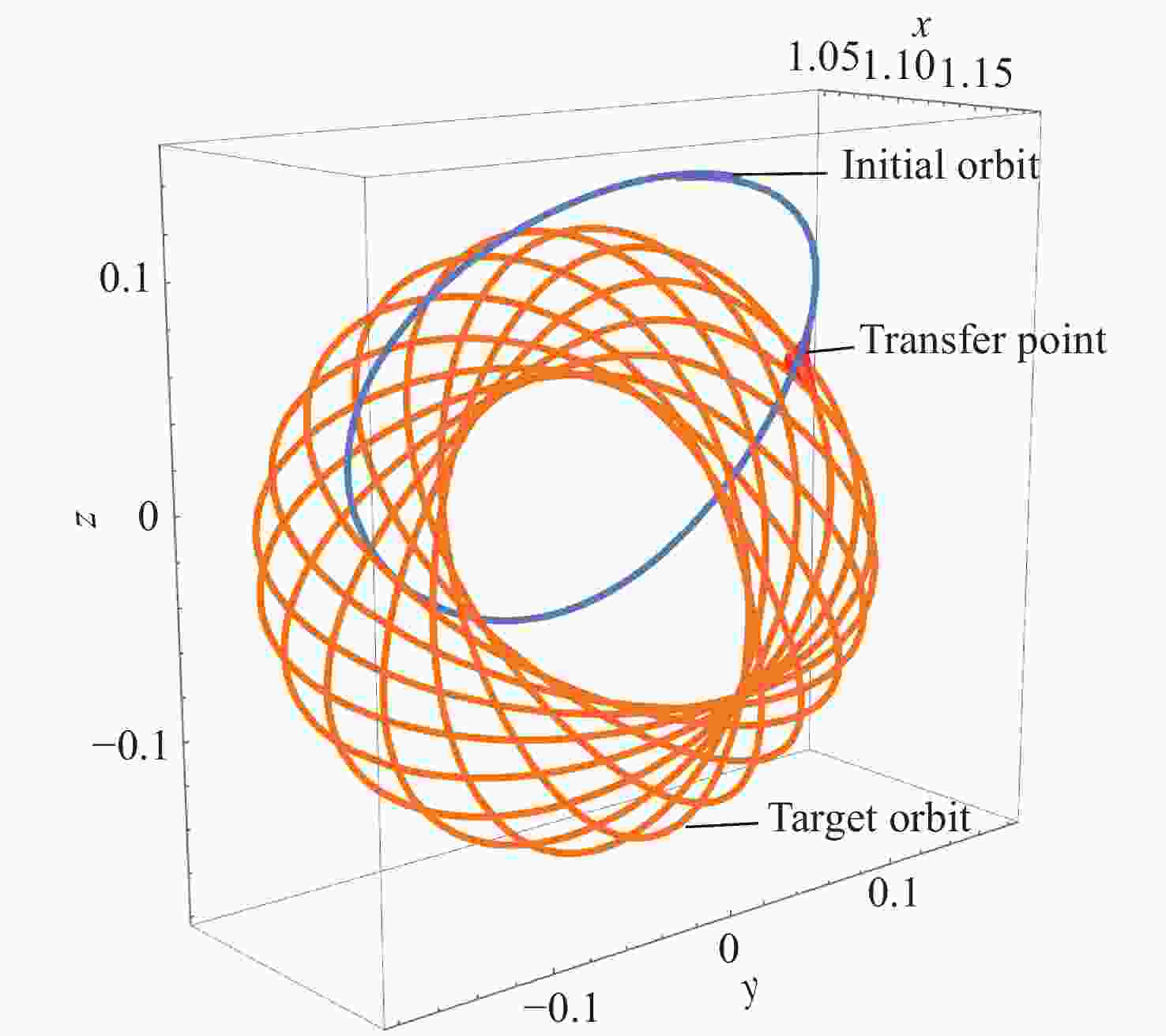
Table 3. Orbital transfer parameter between the halo orbital family
转移参数 转移时间/d 总Δv /(m⋅s–1) 文献数据 7.3048 882.766 间接转移 26.7843 545.899
下载: 导出CSV
-
[1] 雷汉伦, 徐波. 小推力限制性三体系统下稳定平动点附近的高阶解[J]. 中国科学: 技术科学, 2015, 45(11): 1207-1217 doi: 10.1360/N092014-00257LEI Hanlun, XU Bo. High-order solutions around the stable libration points in the low-thrust restricted three-body system[J]. Scientia Sinica Technologica, 2015, 45(11): 1207-1217 doi: 10.1360/N092014-00257 [2] BOOKLESS J, MCINNES C. Control of Lagrange point orbits using solar sail propulsion[J]. Acta Astronautica, 2008, 62(2/3): 159-176 [3] 朱政帆, 高扬. 空间小推力轨道最优Bang-Bang控制的两类延拓解法综述[J]. 深空探测学报, 2017, 4(2): 101-110ZHU Zhengfan, GAO Yang. Survey of two classes of continuation methods for solving optimal Bang-Bang control of low-thrust space trajectories[J]. Journal of Deep Space Exploration, 2017, 4(2): 101-110 [4] KULUMANI S, LEE T. Systematic design of optimal low-thrust transfers for the three-body problem[J]. The Journal of the Astronautical Sciences, 2019, 66(1): 1-31 doi: 10.1007/s40295-018-00139-y [5] 任远, 崔平远, 栾恩杰. 基于标称轨道的小推力轨道设计方法[J]. 吉林大学学报: 工学版, 2006, 36(6): 998-1002REN Yuan, CUI Pingyuan, LUAN Enjie. Low-thrust trajectory design method based on nominal orbit[J]. Journal of Jilin University: Engineering and Technology Edition, 2006, 36(6): 998-1002 [6] HARGRAVES C R, PARIS S W. Direct trajectory optimization using nonlinear programming and collocation[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(4): 338-342 doi: 10.2514/3.20223 [7] HERMAN A L, CONWAY B A. Direct optimization using collocation based on high-order Gauss-Lobatto quadrature rules[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(3): 592-599 doi: 10.2514/3.21662 [8] 孙军伟, 乔栋, 崔平远. 基于SQP方法的常推力月球软着陆轨道优化方法[J]. 宇航学报, 2006, 27(1): 99-102,112 doi: 10.3321/j.issn:1000-1328.2006.01.021SUN Junwei, QIAO Dong, CUI Pingyuan. Study on the optimal trajectories of lunar soft-landing with fixed-thrust using SQP method[J]. Journal of Astronautics, 2006, 27(1): 99-102,112 doi: 10.3321/j.issn:1000-1328.2006.01.021 [9] 朱建丰, 徐世杰. 基于自适应模拟退火遗传算法的月球软着陆轨道优化[J]. 航空学报, 2007, 28(4): 806-812 doi: 10.3321/j.issn:1000-6893.2007.04.007ZHU Jianfeng, XU Shijie. Optimization of lunar soft landing trajectory based on adaptive simulated annealing genetic algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(4): 806-812 doi: 10.3321/j.issn:1000-6893.2007.04.007 [10] FAHROO F, ROSS I M. Direct trajectory optimization by a Chebyshev pseudospectral method[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 160-166 doi: 10.2514/2.4862 [11] PARK B G, TAHK M J. Three-dimensional trajectory optimization of soft lunar landings from the parking orbit with considerations of the landing site[J]. International Journal of Control, Automation and Systems, 2011, 9(6): 1164-1172 doi: 10.1007/s12555-011-0618-0 [12] E Z B, GUZZETTI D. Multi-revolution low-thrust trajectory optimization using symplectic methods[J]. Science China Technological Sciences, 2020, 63(3): 506-519 doi: 10.1007/s11431-019-9511-7 [13] WOOLLANDS R, TAHERI E, JUNKINS L J. Efficient computation of optimal low thrust gravity perturbed orbit transfers[J]. The Journal of the Astronautical Sciences, 2020, 67(2): 458-484 doi: 10.1007/s40295-019-00152-9 [14] CHUPIN M, HABERKORN T, TRÉLAT E. Low-thrust Lyapunov to Lyapunov and halo to halo missions with L2-minimization[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 2017, 51(3): 965-996 doi: 10.1051/m2an/2016044 [15] DU C R, WU K X, STARINOVA O L, et al. Two trajectory configurations for the low-thrust transfer between northern and southern halo orbits in the Earth-Moon system[J]. Advances in Space Research, 2023, 72(10): 4093-4105 doi: 10.1016/j.asr.2023.08.007 [16] 彭坤, 曾豪, 田林, 等. 小推力航天器的地球—火星转移轨道混合设计方法[J]. 航天返回与遥感, 2020, 41(1): 10-17 doi: 10.3969/j.issn.1009-8518.2020.01.002PENG Kun, ZENG Hao, TIAN Lin, et al. Hybrid design method of earth-mars transfer trajectory for low-thrust spacecraft[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 10-17 doi: 10.3969/j.issn.1009-8518.2020.01.002 [17] (周敬, 胡军, 韩铭麟. 共线平动点附近小推力轨道转移中的微分修正技术[J]. 中国科学: 技术科学, 2021, 51(2): 207-220 doi: 10.1360/SST-2020-0140ZHOU Jing, HU Jun, HAN Minglin. Differential correction method in low-thrust orbit transfers near the collinear libration points[J]. Scientia Sinica Technologica, 2021, 51(2): 207-220 doi: 10.1360/SST-2020-0140 [18] SANTOS L B T, SOUSA-SILVA P A, TERRA M O, et al. Optimal transfers from Moon to L2 halo orbit of the Earth-Moon system[J]. Advances in Space Research, 2022, 70(11): 3362-3372 doi: 10.1016/j.asr.2022.08.035 [19] REN Y, SHAN J J. A novel algorithm for generating libration point orbits about the collinear points[J]. Celestial Mechanics and Dynamical Astronomy, 2014, 120(1): 57-75 doi: 10.1007/s10569-014-9560-9 [20] TITOV V B. Zero-velocity surface in the general three-body-problem[J]. Vestnik St. Petersburg University, Mathematics, 2023, 56(1): 125-133 doi: 10.1134/S1063454123010144 [21] 张识, 王攀, 张瑞浩, 等. 选取任意庞加莱截面的新方法[J]. 物理学报, 2020, 69(4): 040503 doi: 10.7498/aps.69.20191585ZHANG Shi, WANG Pan, ZHANG Ruihao, et al. A new method for selecting arbitrary Poincare section[J]. Acta Physica Sinica, 2020, 69(4): 040503 doi: 10.7498/aps.69.20191585 -
-
下载:
计量
- 文章访问数: 295
- HTML全文浏览量: 89
- PDF下载量: 37
-
被引次数:
0(来源:Crossref)
0(来源:其他)
