基于非线性特性的空间站转位机构拓扑优化
doi: 10.11728/cjss2024.05.2023-0087 cstr: 32142.14.cjss2024.05.2023-0087
-
刘汉武 男, 1986年5月出生于四川绵阳市, 现为上海宇航系统工程研究所、宇航空间机构全国重点实验室高级工程师, 主要研究方向为结构与机构动力学、非线性动力学和拓扑优化分析等. E-mail: jingxi105@163.com -
张华 男, 1977年10月生, 现为上海宇航系统工程研究所、宇航空间机构全国重点实验室研究员, 研究方向为系统动力学与控制、复杂空间结构机构设计与优化等. E-mail: ases_zhang@163.com
作者简介:
通讯作者:
Topological Optimization of Spatial Indexing Mechanisms Based on Nonlinear Characteristics
-
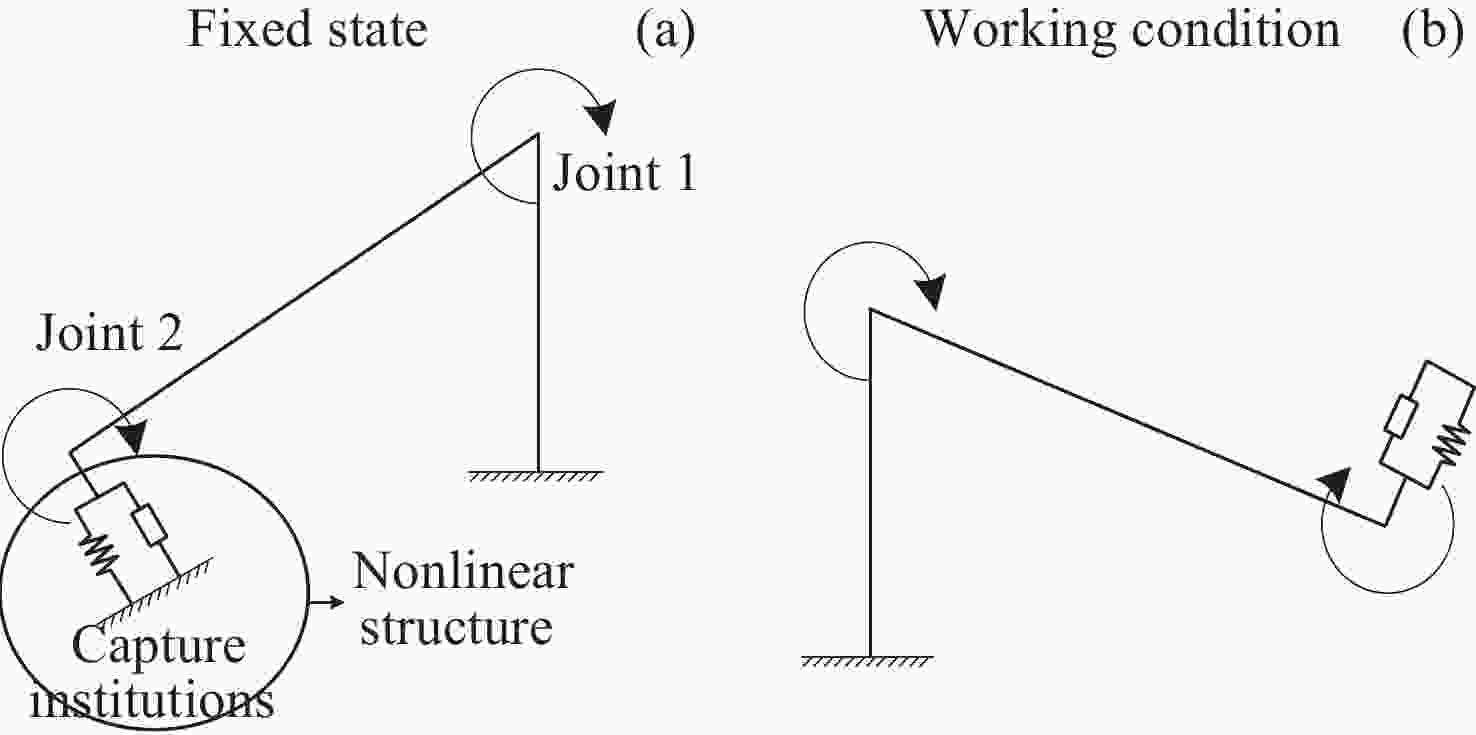
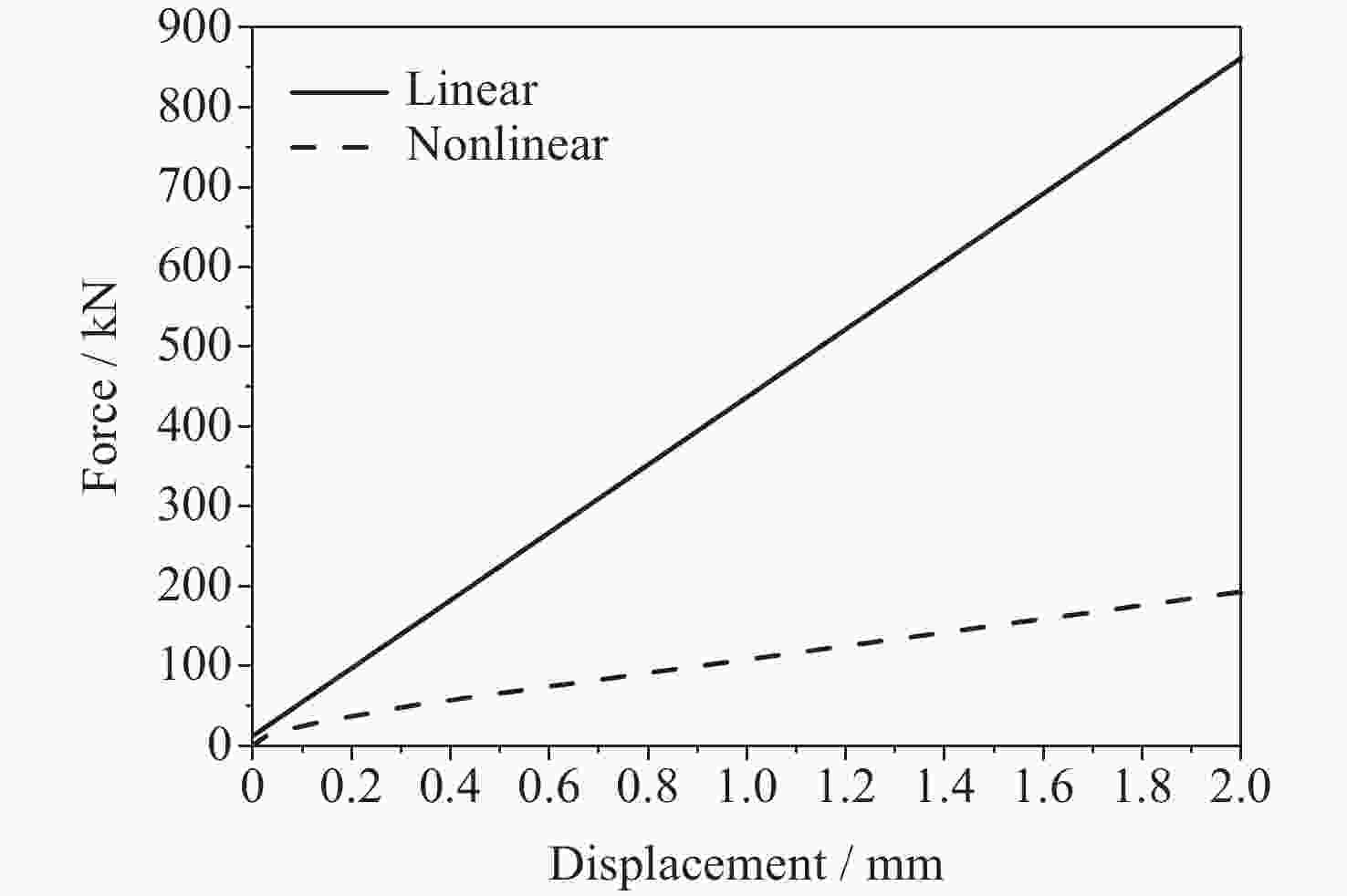
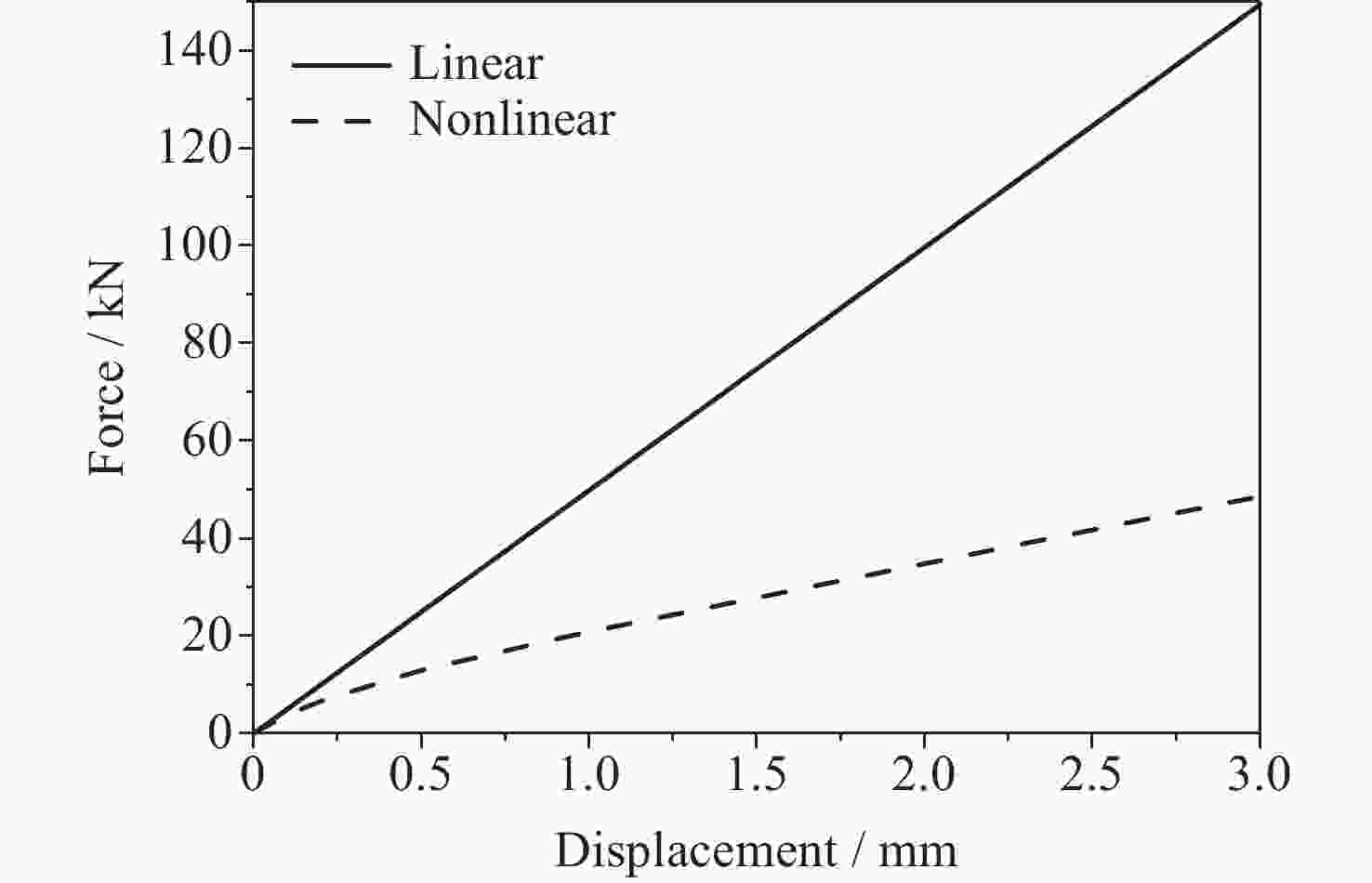
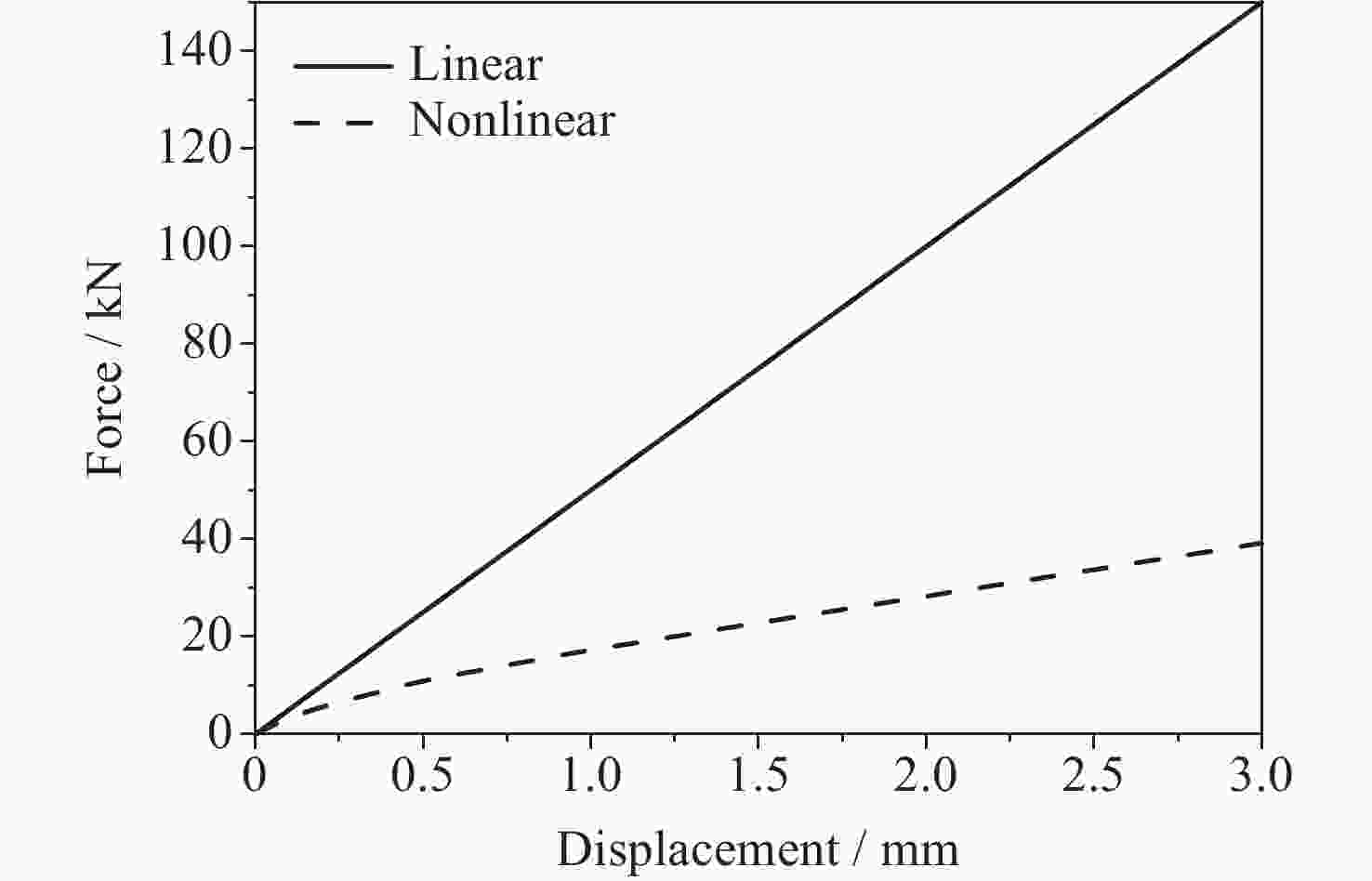
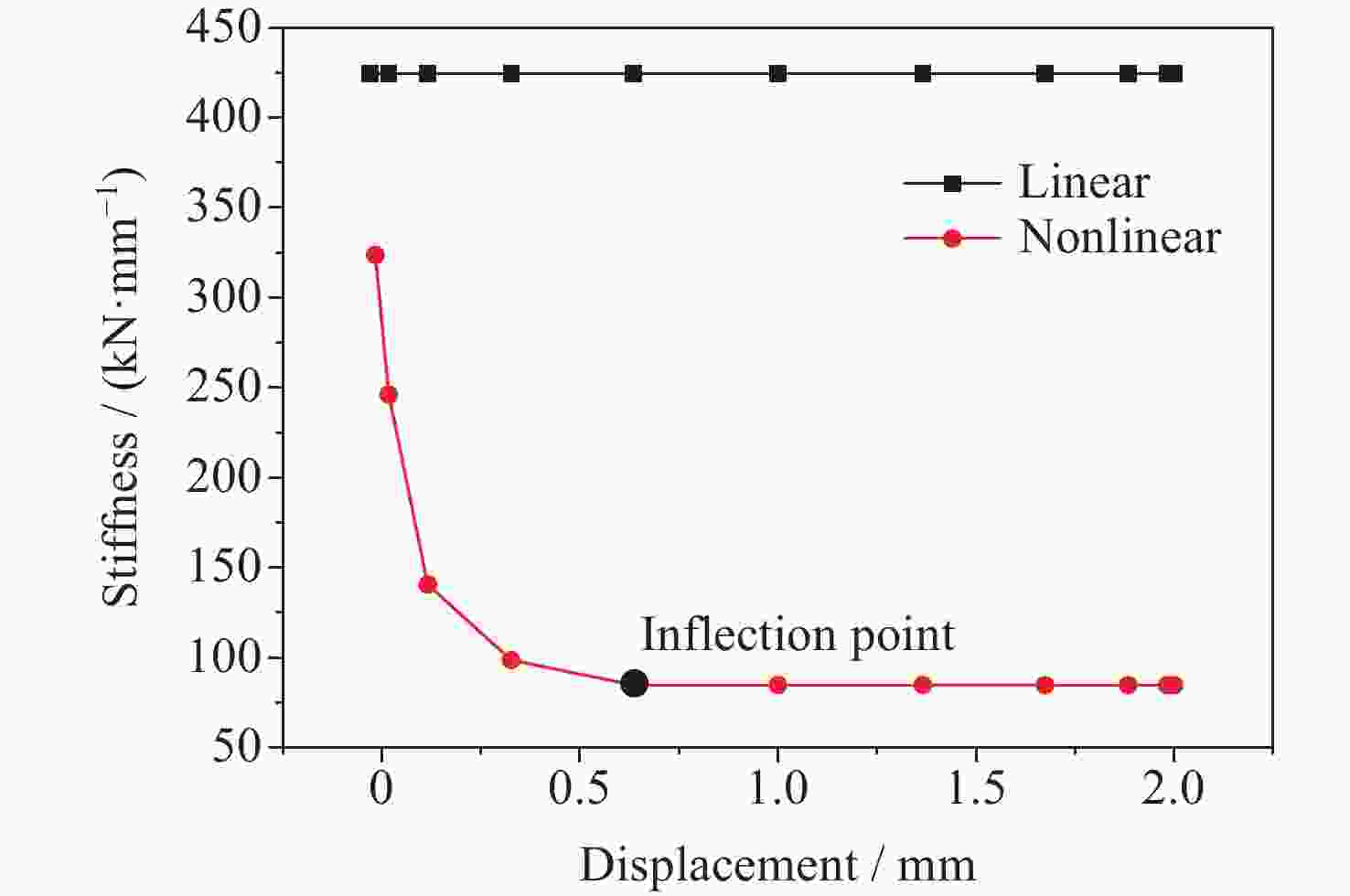
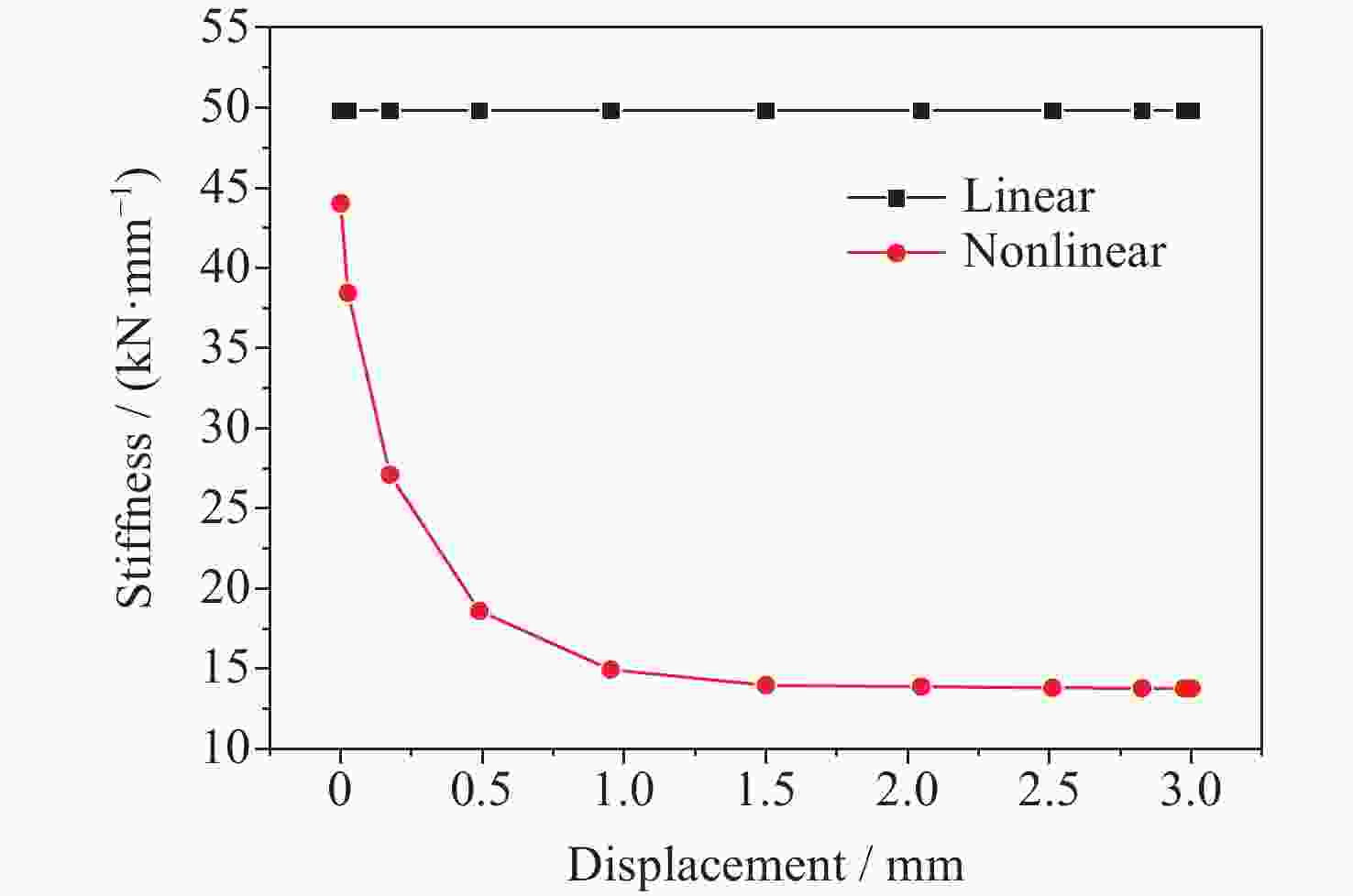
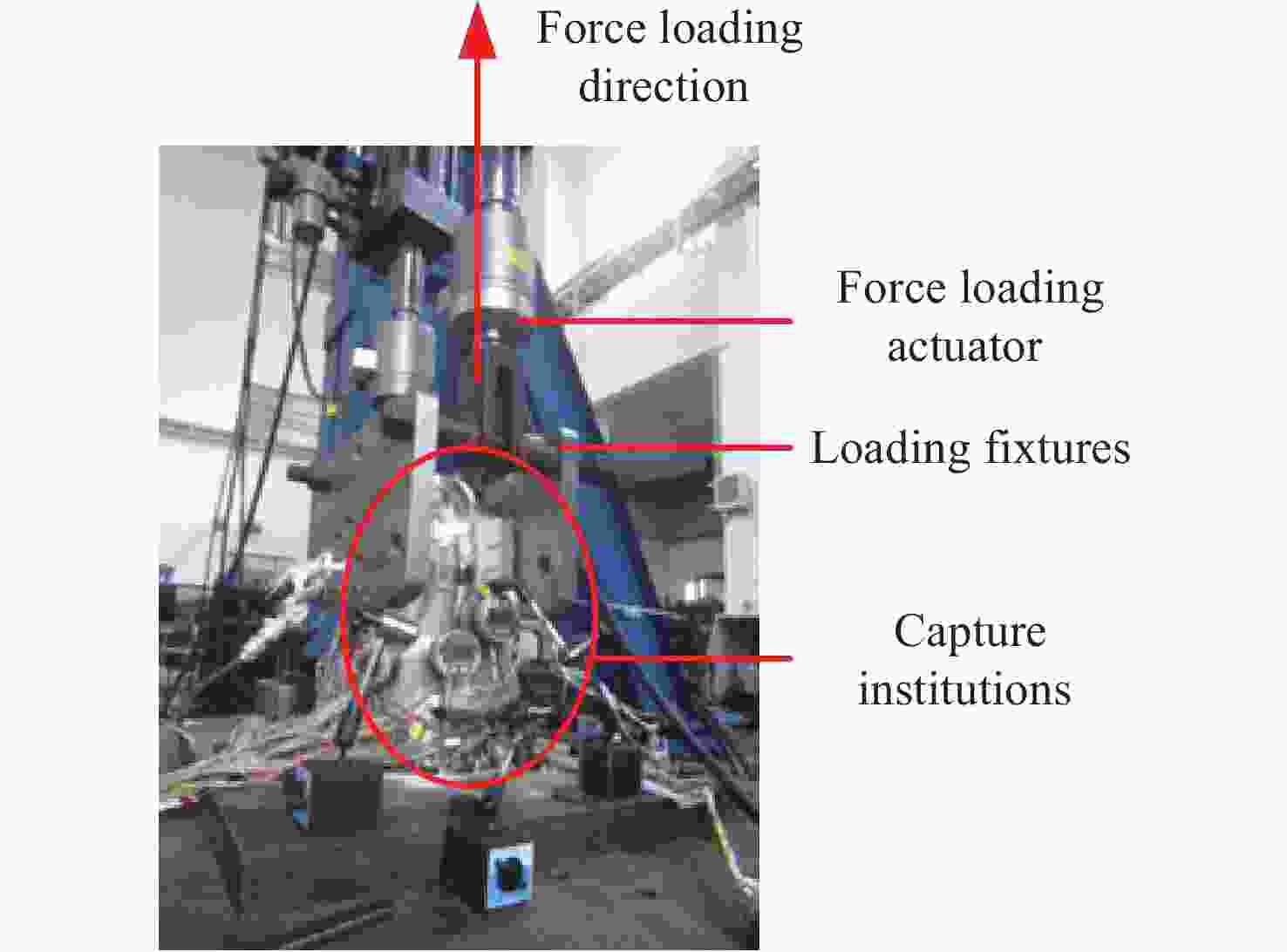
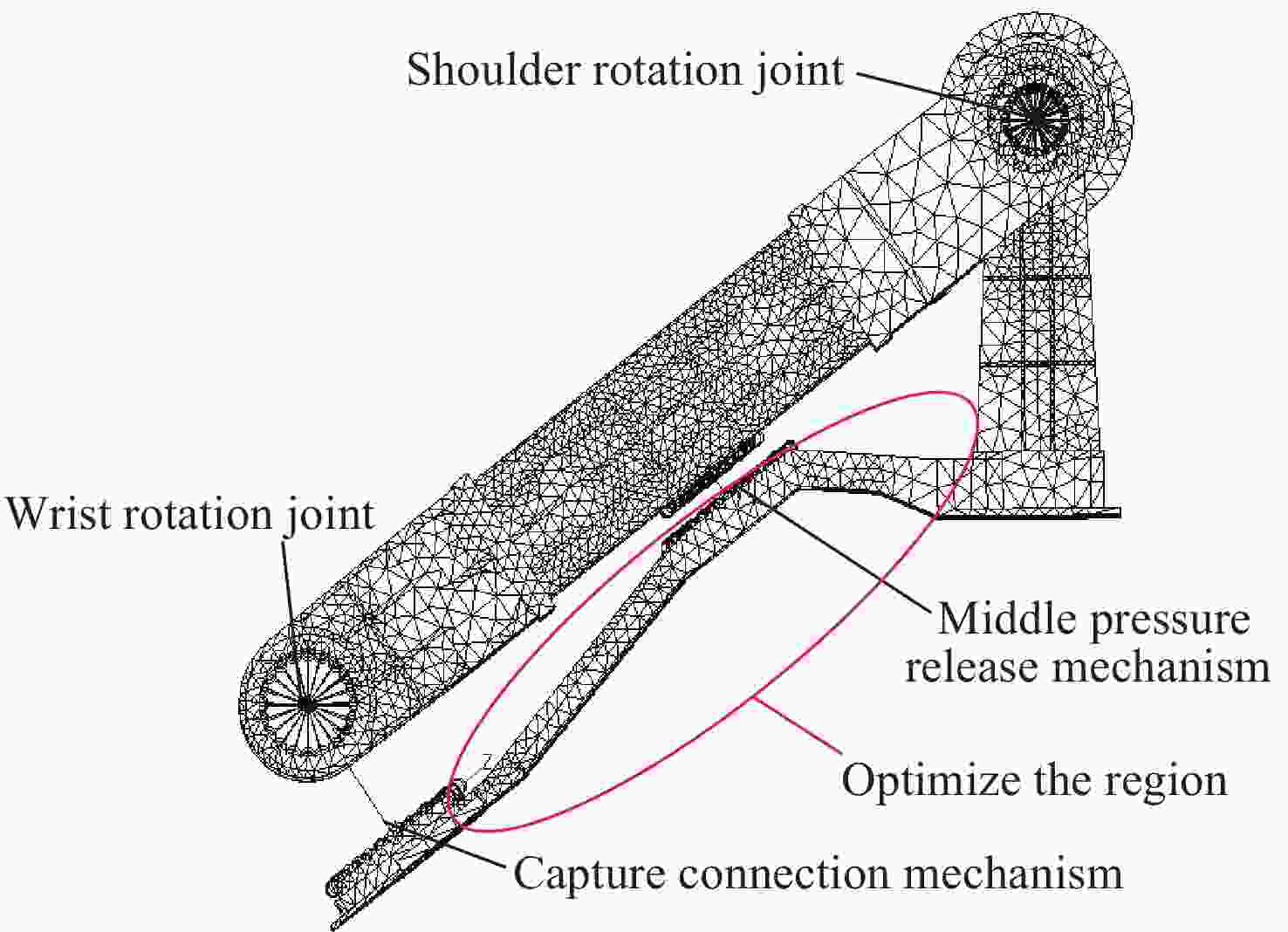
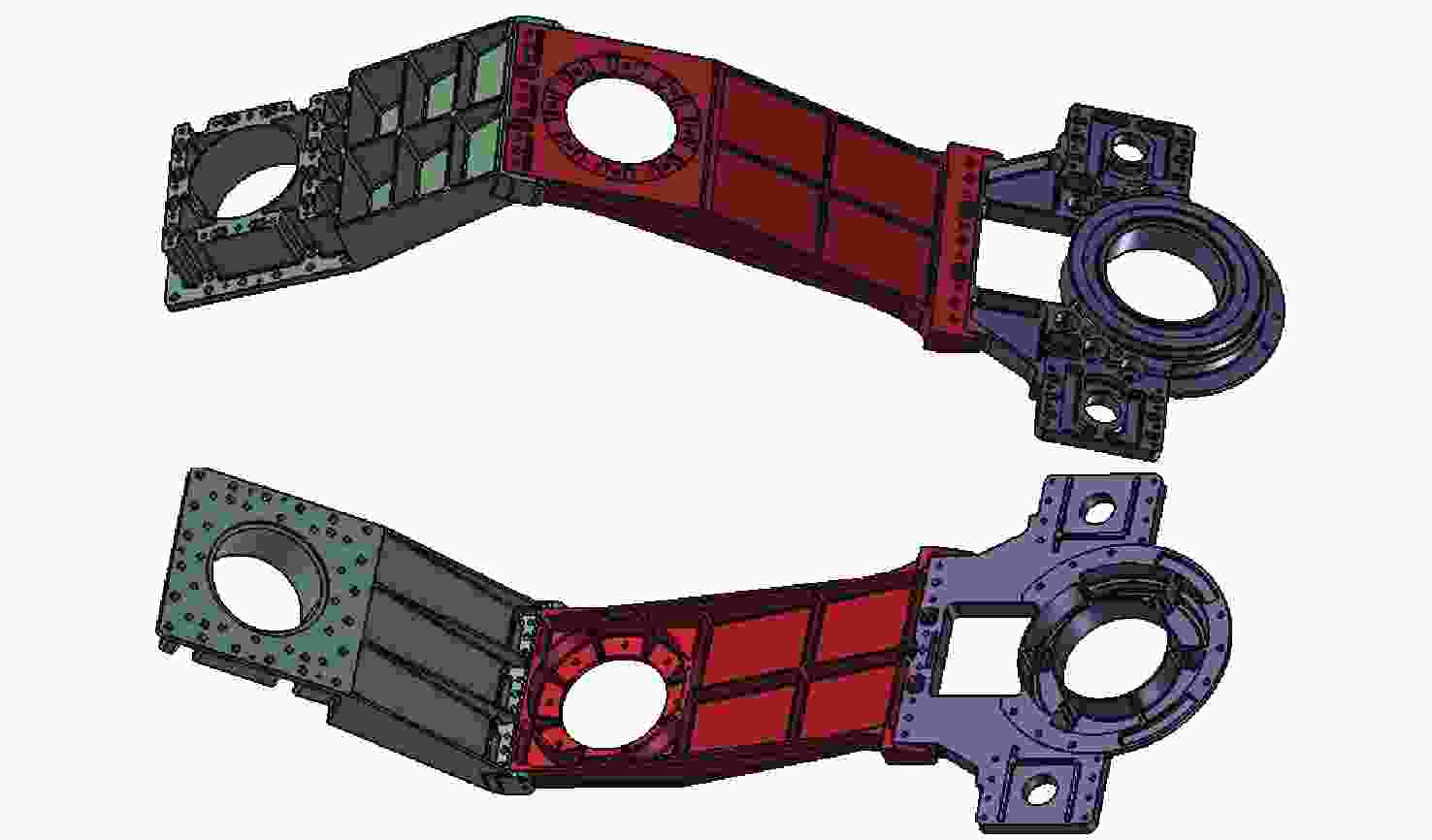
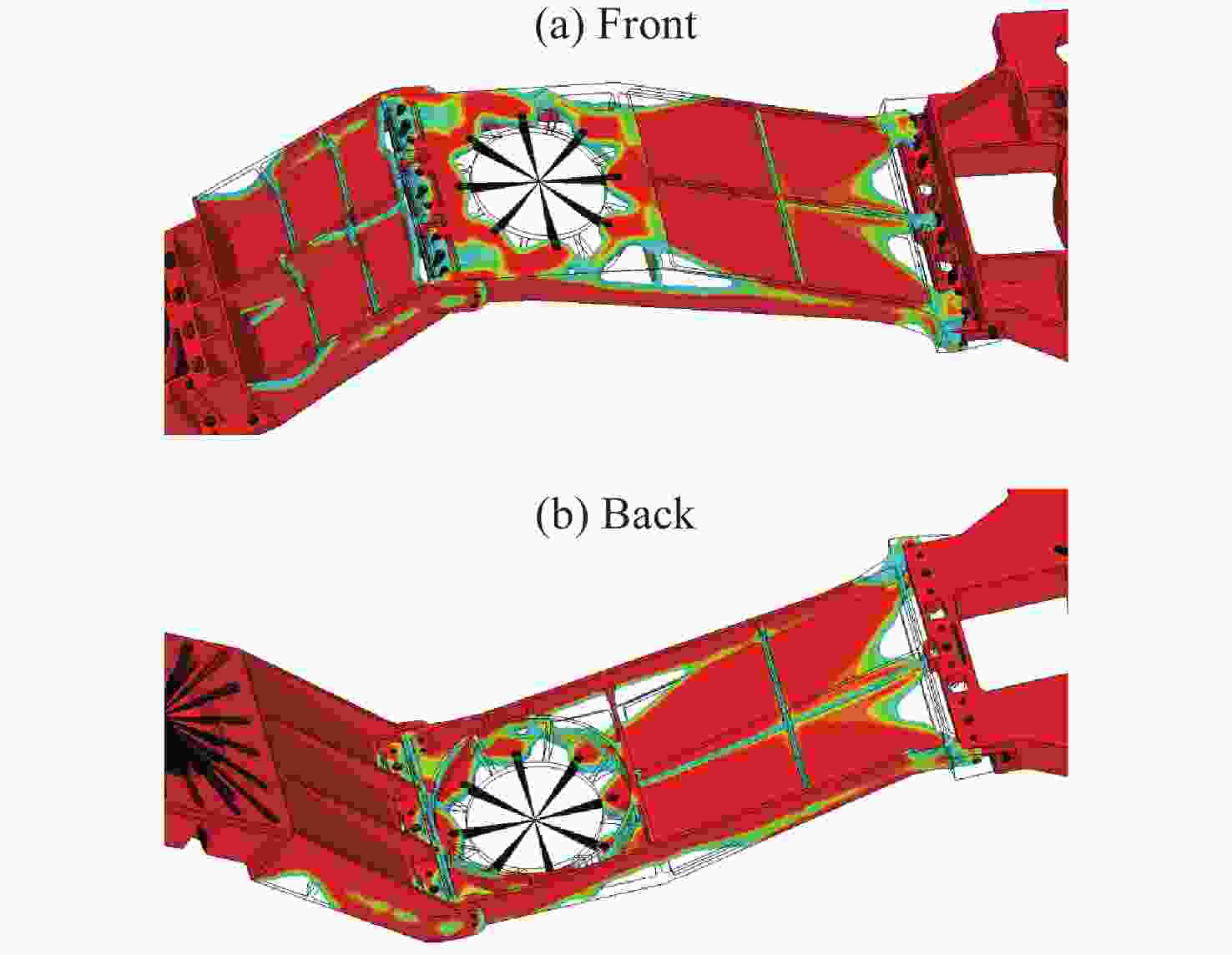
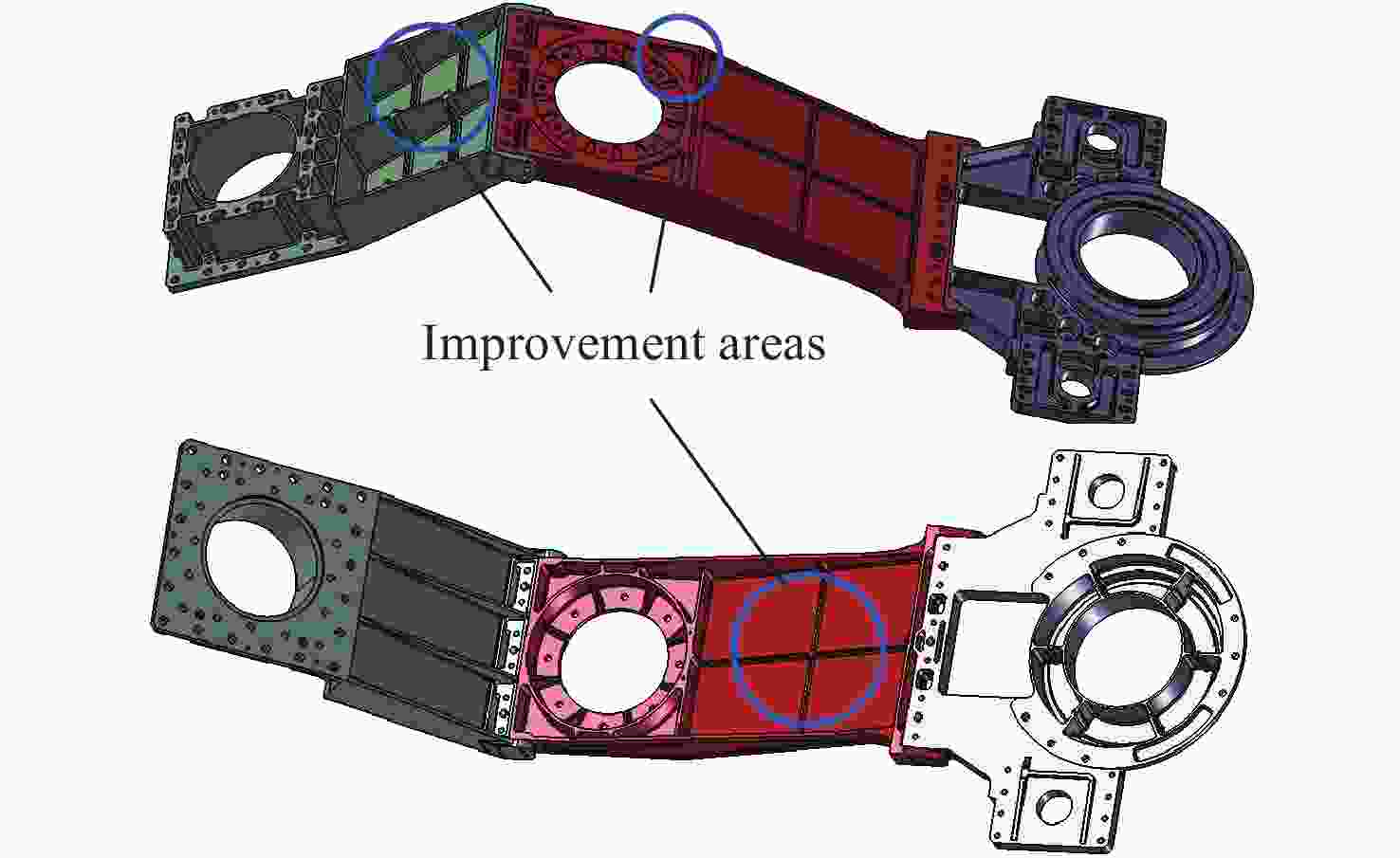
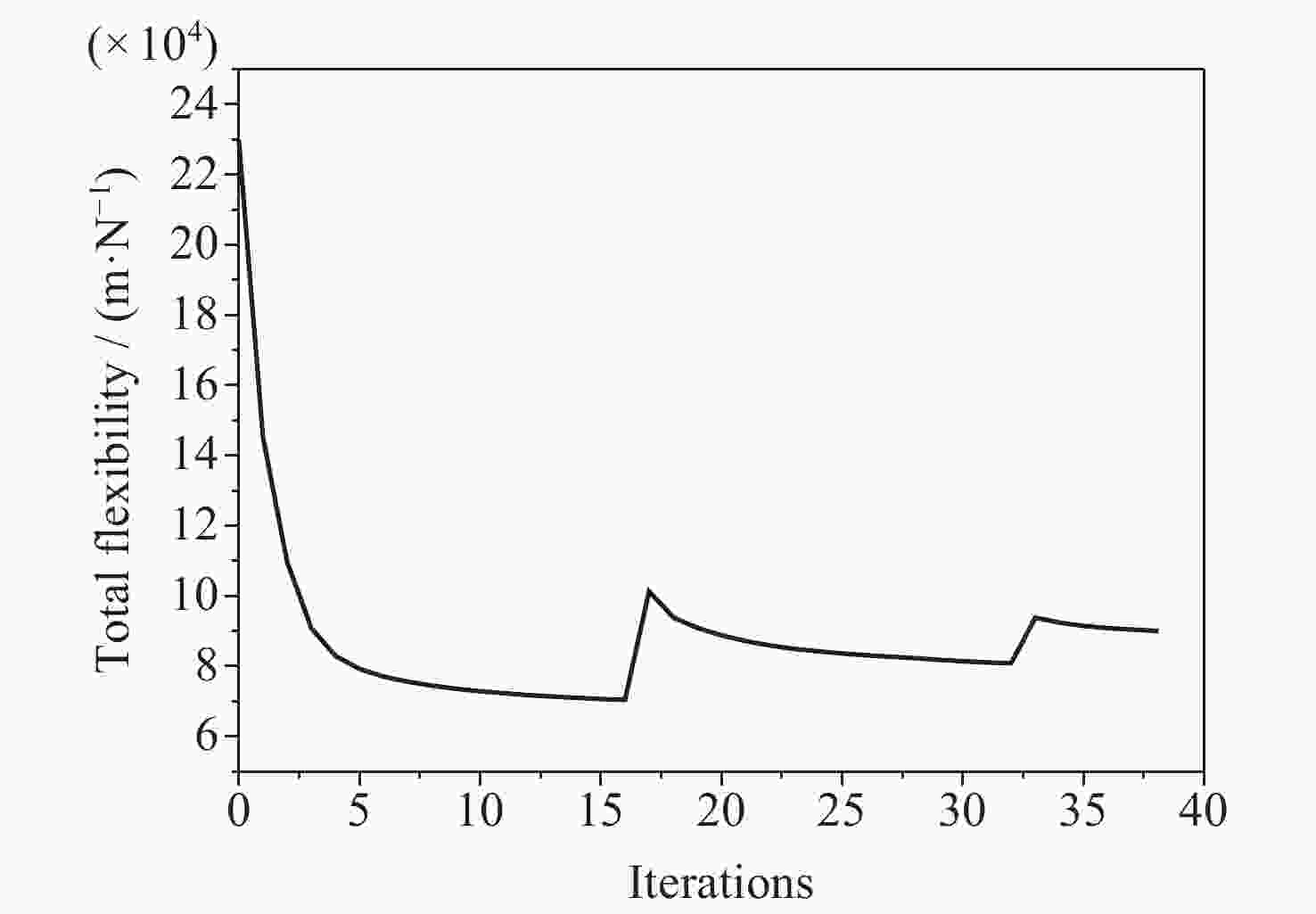
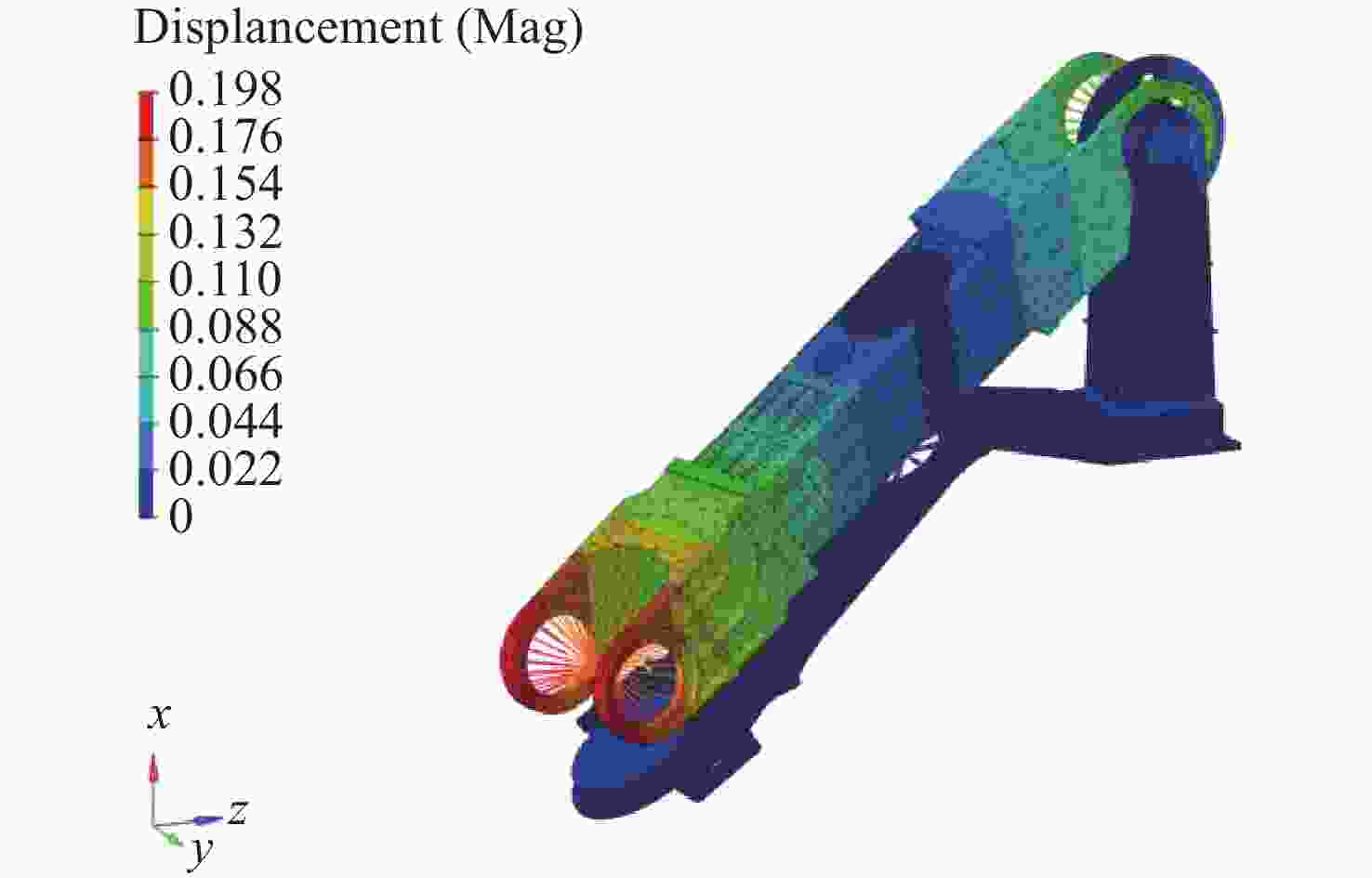
摘要: 针对含非线性特性的空间站转位机构轻量化设计问题, 建立了考虑非线性特性的结构/机构拓扑优化分析方法, 通过模拟静力试验过程方法得到其力–位移曲线, 按照特定的原则提取出非线性结构的等效刚度, 得出转位机构捕获连接机构考虑非线性特性的分析结果与静刚度试验结果误差在10%以内, 满足工程实际应用需要, 说明了捕获连接机构非线性刚度分析方法的可行性. 采用变密度法(SIMP), 建立了含非线性特性的转位机构拓扑优化模型, 开展了空间站转位机构中间支架拓扑优化分析和减重设计, 结构减重24%. 分析结果表明, 转位机构满足刚度和强度要求, 实现了空间站转位机构轻量化设计的目标, 说明了该分析方法的有效性. 本研究建立的含局部非线性特性的拓扑优化分析方法为空间站转位机构轻量化设计提供了解决途径, 也为其他非线性结构机构拓扑优化提供了参考, 同时为中国空间站重点工程项目的建设提供了技术支撑.Abstract: For the lightweight design of the space station transfer mechanism with nonlinear characteristics, a structural/mechanism topology optimization method considering nonlinear characteristics was established, and the force-displacement curve was obtained by simulating the static test process. The equivalent stiffness of the nonlinear structure was extracted according to a specific principle, which could match the test results well. The topology optimization analysis and weight reduction design of the intermediate bracket of the space station transfer mechanism were carried out using the method of Solid Isotropic Material with Penalization (SIMP), and the structure was reduced by 24%, achieving the goal of lightweight design for the space station transfer mechanism. This shows the effectiveness of the analysis method. The topology optimization method established for the lightweight design of the space station transfer mechanism with local nonlinear characteristics provides a solution for the lightweight design of other nonlinear structure mechanisms, and also provides a reference for other nonlinear structure mechanisms. As the demand for advanced materials and structures with improved performance continues to grow, the topology optimization method established for the space station transfer mechanism will serve as a valuable tool for engineers working in various fields. For example, it can be applied to the development of lightweight automobiles, aircraft, and spacecraft, as well as to the design of renewable energy systems, robotics, and other advanced technologies. By incorporating the method into their design processes, engineers can create more innovative and efficient products that will help to drive progress and advancements in these industries. In conclusion, the topology optimization method developed for the lightweight design of the space station transfer mechanism with local nonlinear characteristics has demonstrated its effectiveness and versatility in addressing complex engineering design challenges. By providing a systematic approach to the design process that considers both structural and mechanical properties, this method has the potential to impact various industries and applications, contributing to the development of more advanced and sustainable structures and mechanisms for years to come.
-
Key words:
- Chinese space station /
- Transposition mechanism /
- Nonlinear /
- Stiffness /
- Topology optimization
-
图 4 捕获机构非线性模型及加载坐标
Figure 4. Capture the nonlinear model and loading coordinates of the mechanism
图 11 捕获连接机构静刚度试验
Figure 11. Capture the static stiffness test of the connection mechanism
图 12 x方向位移–刚度曲线试验与对比
Figure 12. Comparison of x-axis stiffness-displacement curve testing and analysis
图 13 y方向位移–刚度曲线试验与对比
Figure 13. Comparison of y-axis stiffness-displacement curve testing and analysis
图 14 z方向位移–刚度曲线试验与对比
Figure 14. Comparison of z-axis stiffness-displacement curve testing and analysis
图 15 空间站转位机构分析模型
Figure 15. Analysis model of the space station’s transposition mechanism
图 20 转位机构基频44.2 Hz
Figure 20. Sublocation mechanism has a fundamental frequency of 44.2 Hz
表 1 分析刚度值 (单位: kN·mm–1)
Table 1. Analysis values of the stiffness (Unit: kN·mm–1)
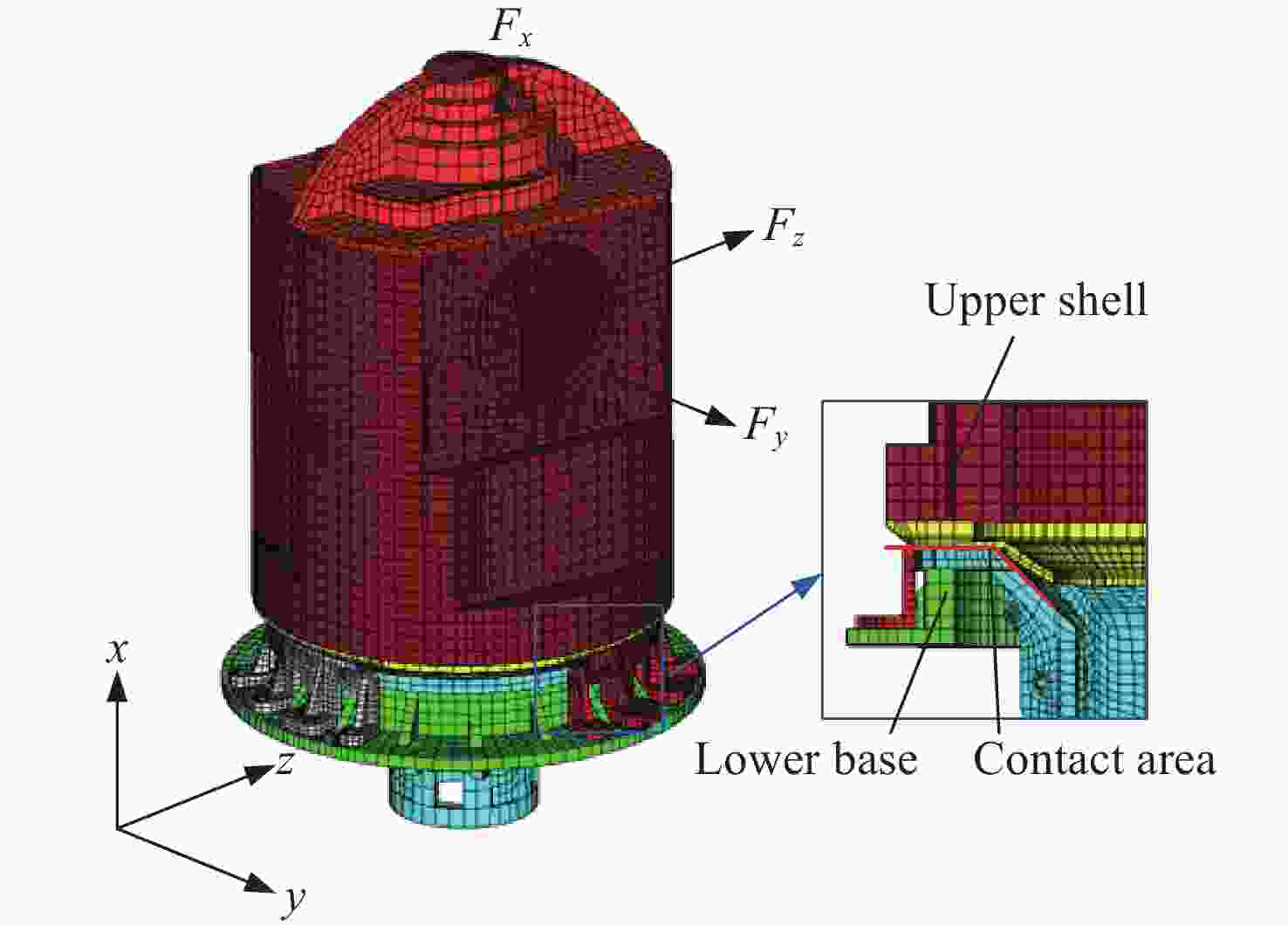
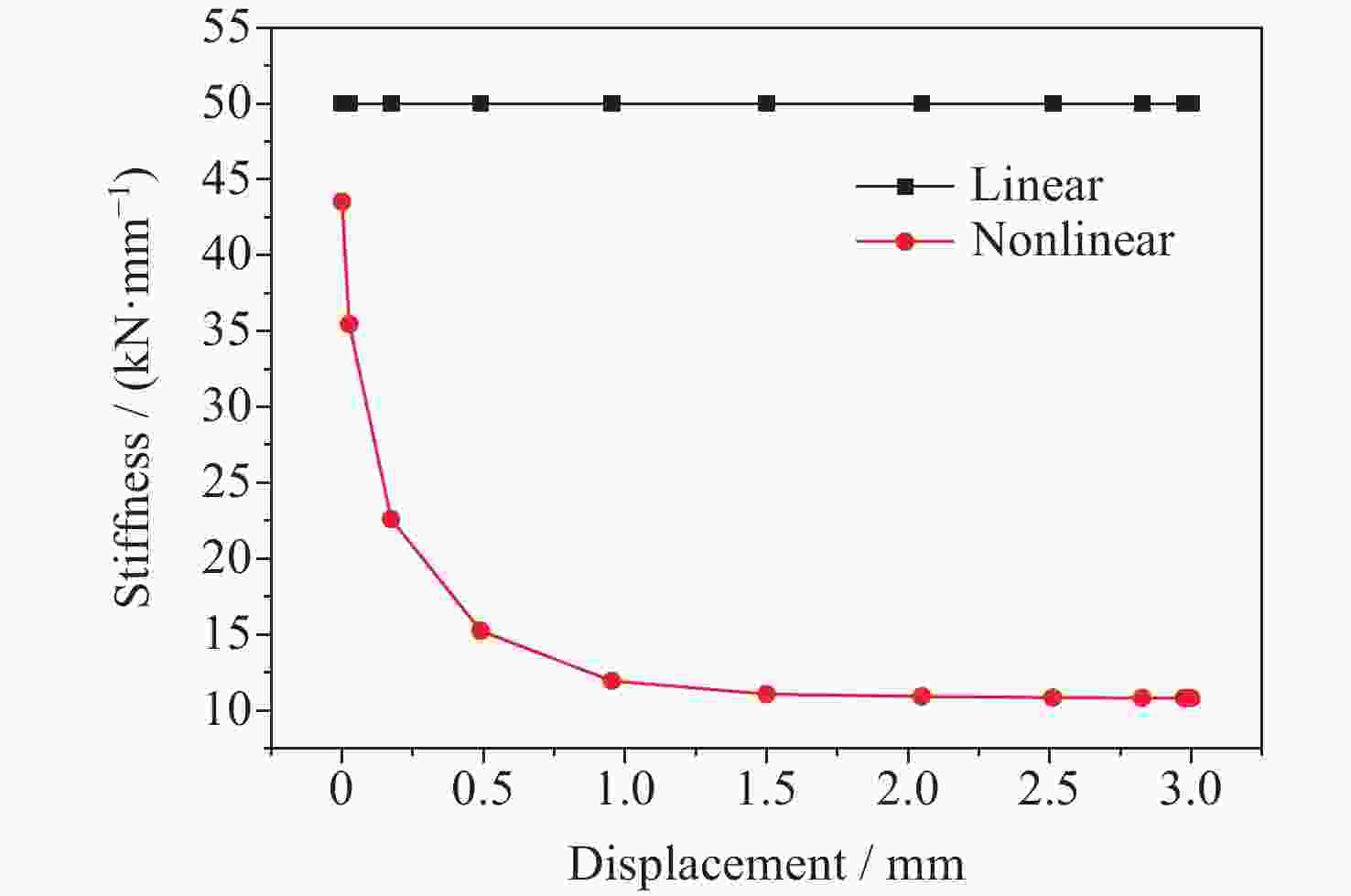
工况 线性 非线性 Px 424.5 84.6 Py 49.8 13.8 Pz 50.0 10.8 
下载: 导出CSV
表 2 刚度值对比
Table 2. Comparison of stiffness values
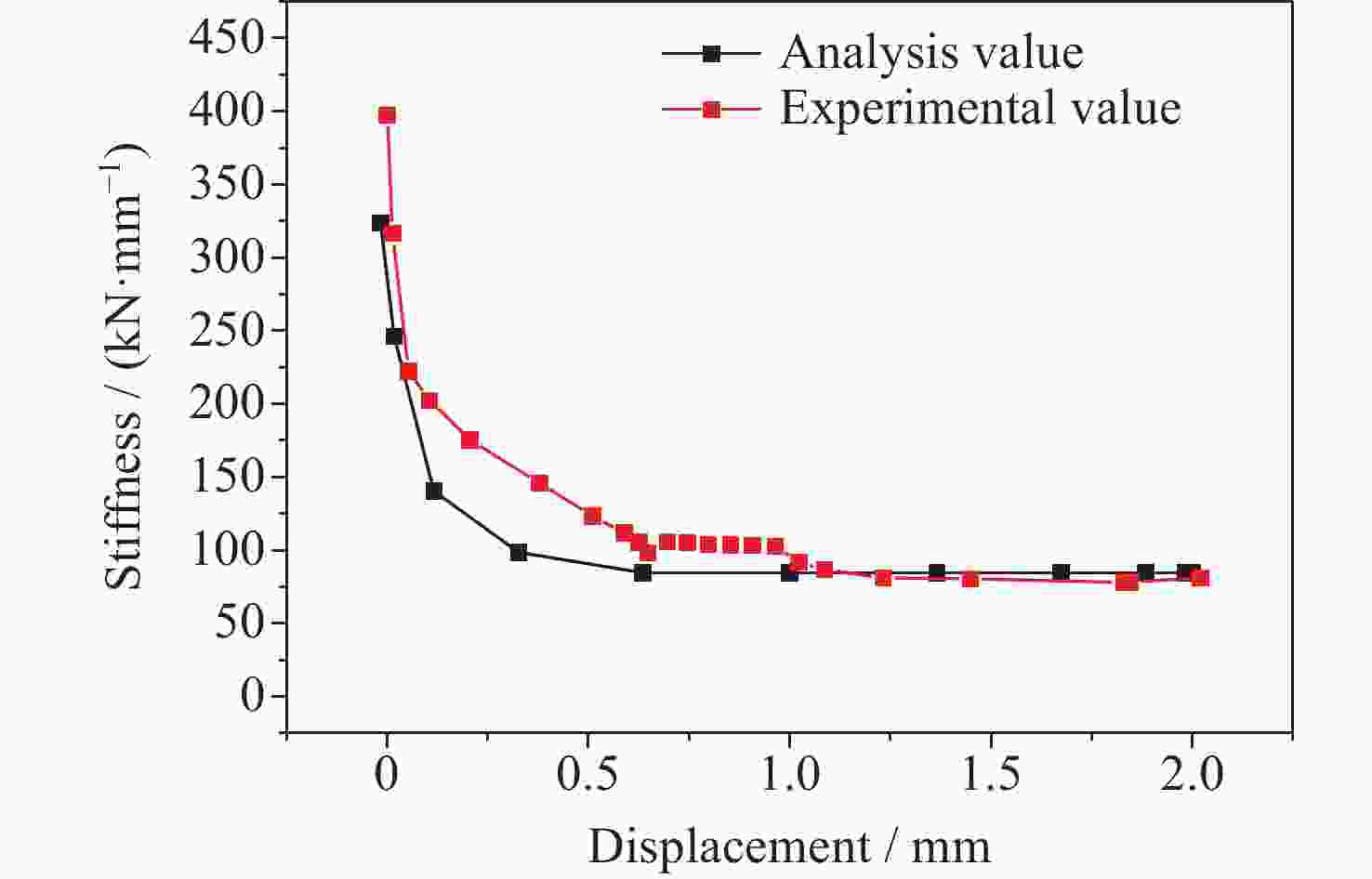
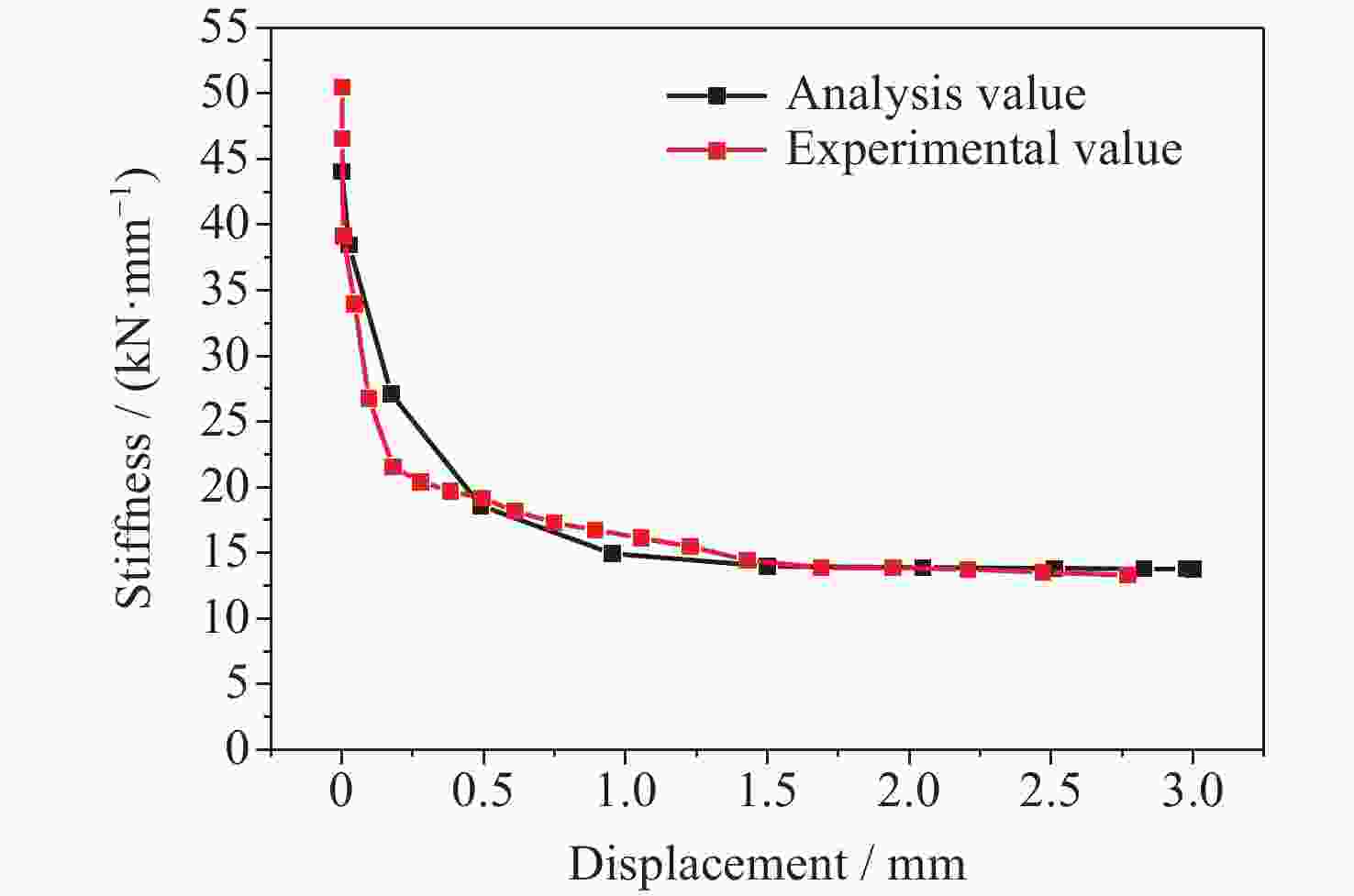
工况 刚度/(kN·mm–1) 误差/(%) 分析值 试验值 Px 84.6 78.1 8.3 Py 13.8 13.3 3.8 Pz 10.8 11.6 –6.9
下载: 导出CSV
-
[1] BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635-654 [2] SUI Y K, YANG D Q. A new method for structural topological optimization based on the concept of independent continuous variables and smooth model[J]. Acta Mechanica Sinica, 1998, 14(2): 179-185 doi: 10.1007/BF02487752 [3] XIE Y M, STEVEN G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures, 1993, 49(5): 885-896 [4] 蒋垣腾, 赵敏. 基于参数化水平集方法的水下耐压结构的拓扑优化[J]. 船舶力学, 2022, 26(3): 400-413JIANG Yuanteng, ZHAO Min. Topology optimization of underwater pressure structure design with parametric level set method[J]. Journal of Ship Mechanics, 2022, 26(3): 400-413 [5] 徐世鹏, 丁晓红, 段朋云, 等. 考虑时变刚度特性的复合材料微结构拓扑优化设计方法[J]. 力学学报, 2022, 54(1): 134-146XU Shipeng, DING Xiaohong, DUAN Pengyun, et al. Topology optimization of composite material microstructure considering time-changeable stiffness[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(1): 134-146 [6] 季晓彤, 解立垚, 王坤, 等. 基于拓扑优化的新型热沉翅片结构设计[J]. 河北工业大学学报, 2022, 51(1): 61-67,87JI Xiaotong, XIE Liyao, WANG Kun, et al. Topology optimization of heat sink structure based on variable density method[J]. Journal of Hebei University of Technology, 2022, 51(1): 61-67,87 [7] 刘宏亮, 付玲. 一种考虑载荷周期分解疲劳寿命计算的结构拓扑优化方法[J]. 中国工程机械学报, 2022, 20(1): 22-29LIU Hongliang, FU Ling. A load cycle decomposition based fatigue calculation considered structural topology optimization method[J]. Chinese Journal of Construction Machinery, 2022, 20(1): 22-29 [8] 侯亮, 柴象海, 白国娟, 等. 航空发动机短舱泄压门冲击载荷结构拓扑优化技术研究[J]. 航空科学技术, 2022, 33(1): 58-65HOU Liang, CHAI Xianghai, BAI Guojuan, et al. Research on topology optimization technology of shock loading structure of aeroengine nacelle relief valve[J]. Aeronautical Science & Technology, 2022, 33(1): 58-65 [9] 吴书豪, 张永存, 刘书田. 考虑瞬态效应的承载隔热多功能结构拓扑优化[J]. 计算力学学报, 2022, 39(2): 142-149 doi: 10.7511/jslx20201016001WU Shuhao, ZHANG Yongcun, LIU Shutian. Topology optimization for multi-functional structure with both load-bearing and thermal insulation capability considering transient effect[J]. Chinese Journal of Computational Mechanics, 2022, 39(2): 142-149 doi: 10.7511/jslx20201016001 [10] 李孔伟, 徐宝亮, 罗益, 等. 基于不确定理论帐篷框架可靠性拓扑优化设计[J]. 机械强度, 2022, 44(2): 348-355LI Kongwei, XU Baoliang, LUO Yi, et al. Topology optimization design of reliability strategy for tent frame based on uncertainty theory[J]. Journal of Mechanical Strength, 2022, 44(2): 348-355 [11] 王天舒, 孔宪仁, 王本利, 等. 含铰间间隙的航天器附件展开过程分析[J]. 哈尔滨工业大学学报, 2001, 33(3): 283-286WANG Tianshu, KONG Xianren, WANG Benli, et al. Analysis of deployment of spacecraft appendages with hinge gap[J]. Journal of Harbin Institute of Technology, 2001, 33(3): 283-286 [12] 徐小胜, 于登云, 曲广吉. 柔性航天器自由飞行状态系统基频的估算方法[J]. 宇航学报, 2004, 25(2): 208-212XU Xiaosheng, YU Dengyun, QU Guangji. The natural frequency calculating for flexible spacecraft in free flight[J]. Journal of Astronautics, 2004, 25(2): 208-212 [13] 徐超, 杨旭辉, 张铎. 螺栓连接梁的非线性动力学响应分析[J]. 强度与环境, 2011, 38(2): 1-5XU Chao, YANG Xuhui, ZHANG Duo. Study on nonlinear dynamic response of bolted jointed beam[J]. Structure & Environment Engineering, 2011, 38(2): 1-5 [14] SONG Y, HARTWIGSEN C J, MCFARLAND D M, et al. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements[J]. Journal of Sound and Vibration, 2004, 273(1/2): 249-276 -
-
下载:
计量
- 文章访问数: 334
- HTML全文浏览量: 150
- PDF下载量: 29
-
被引次数:
0(来源:Crossref)
0(来源:其他)
