面向空间引力波探测检验质量捕获的弹性管模型预测控制
doi: 10.11728/cjss2025.01.2024-0009 cstr: 32142.14.cjss.2024-0009
-
贺雄峰 男, 1999年9月出生于贵州省, 在同济大学电子与信息工程学院获得学士学位, 在中国科学院微小卫星创新研究院攻读硕士学位, 主要研究方向为基于模型预测控制的无拖曳控制方法研究. E-mail: hexiongfeng@mail.ustc.edu.cn -
张永合 男, 1977年出生于山东省, 博士毕业于中国科学院大学, 主要从事航天器导航、制导与控制、时频多体动力学等方向研究, 特别是在航天器系统设计与仿真、引力波探测无拖曳编队控制等领域进行了深入的研究. E-mail: zhangyh@microsate.com
作者简介:
通讯作者:
Elastic Tube Model Predictive Control for Test Mass Capture for Space-borne Gravitational Wave Detection
-
摘要: 在空间引力波探测任务中, 检验质量稳定捕获是航天器进入超稳飞行状态的关键步骤. 该过程存在初始误差大、系统不确定性大、执行约束强等特点. 提出了一种基于弹性管模型预测控制的检验质量捕获控制方法, 基于滚动优化和弹性管道技术的控制结构, 提高捕获成功率, 并且充分补偿卫星对检验质量的耦合干扰; 利用小容差有效集法, 提高在线计算的求解精度, 确保检验质量的高控制精度; 同时基于特征工程方法的最小鲁棒正不变集离线修正方法, 减少基于Minkowski求和得到的最小鲁棒正不变集顶点数, 降低了在线计算复杂度. 利用该方法在航天器–双检验质量全自由度仿真平台上进行仿真验证, 结果表明控制效果满足检验质量捕获精度要求, 控制器具有鲁棒性且有效提高了收敛速度, 抑制了平台运动干扰和量测噪声的影响.
-
关键词:
- 无拖曳控制 /
- 检验质量捕获 /
- 弹性管道模型预测控制 /
- 干扰补偿
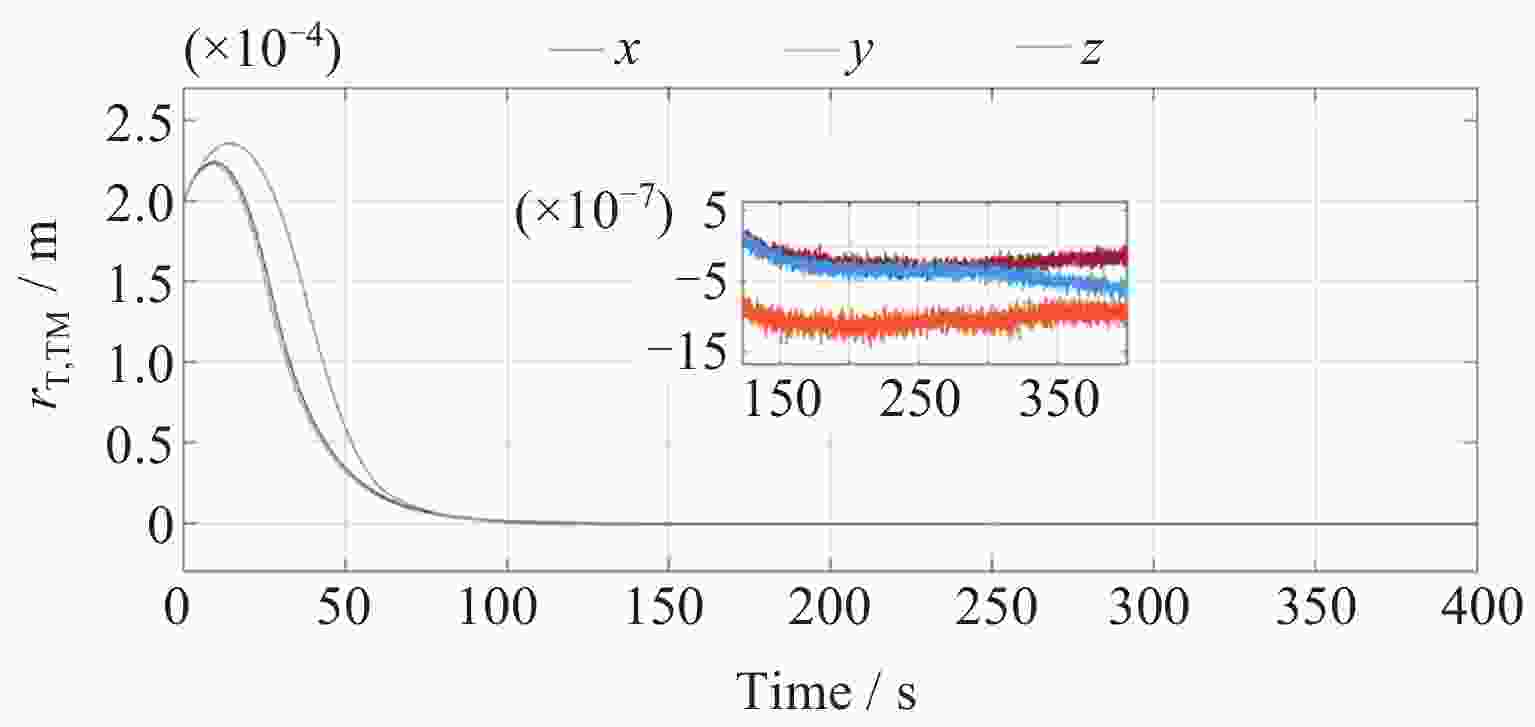
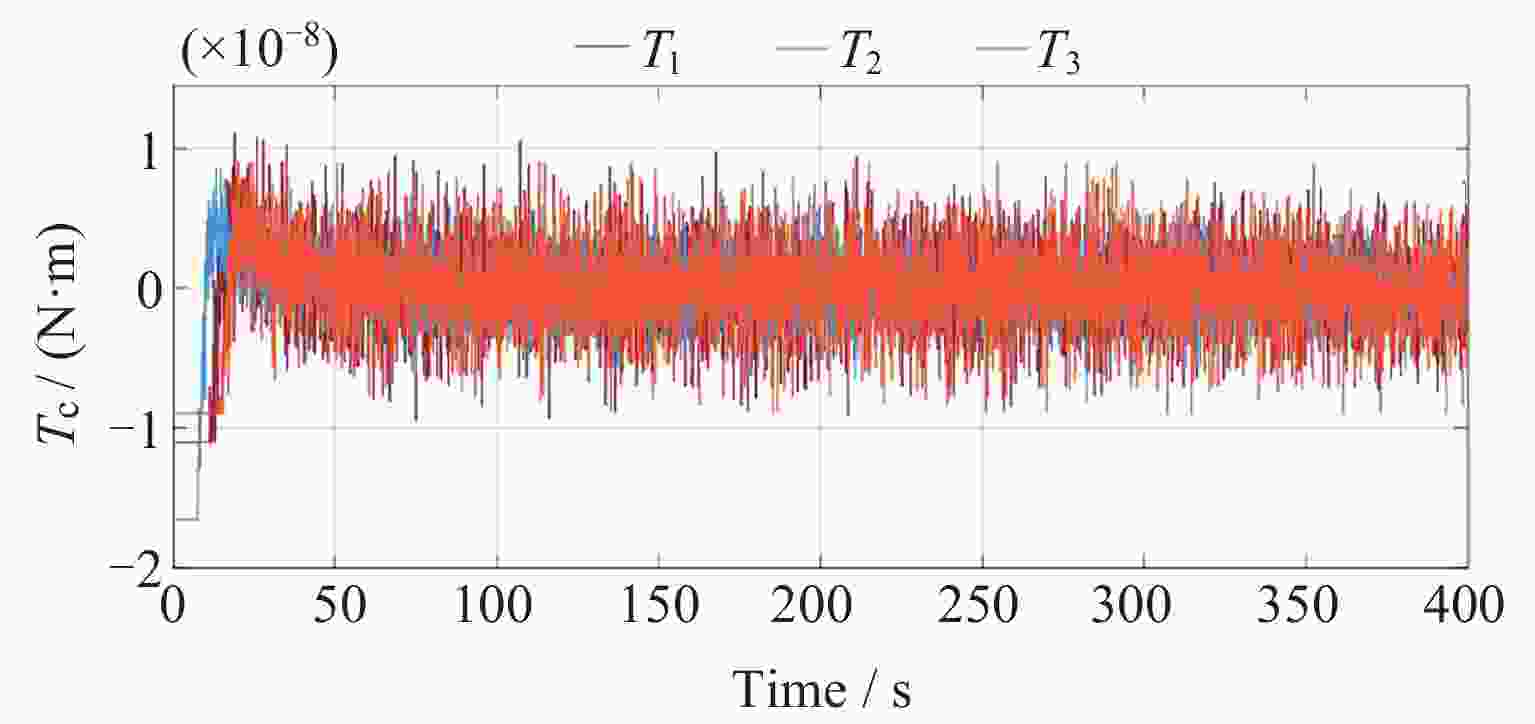
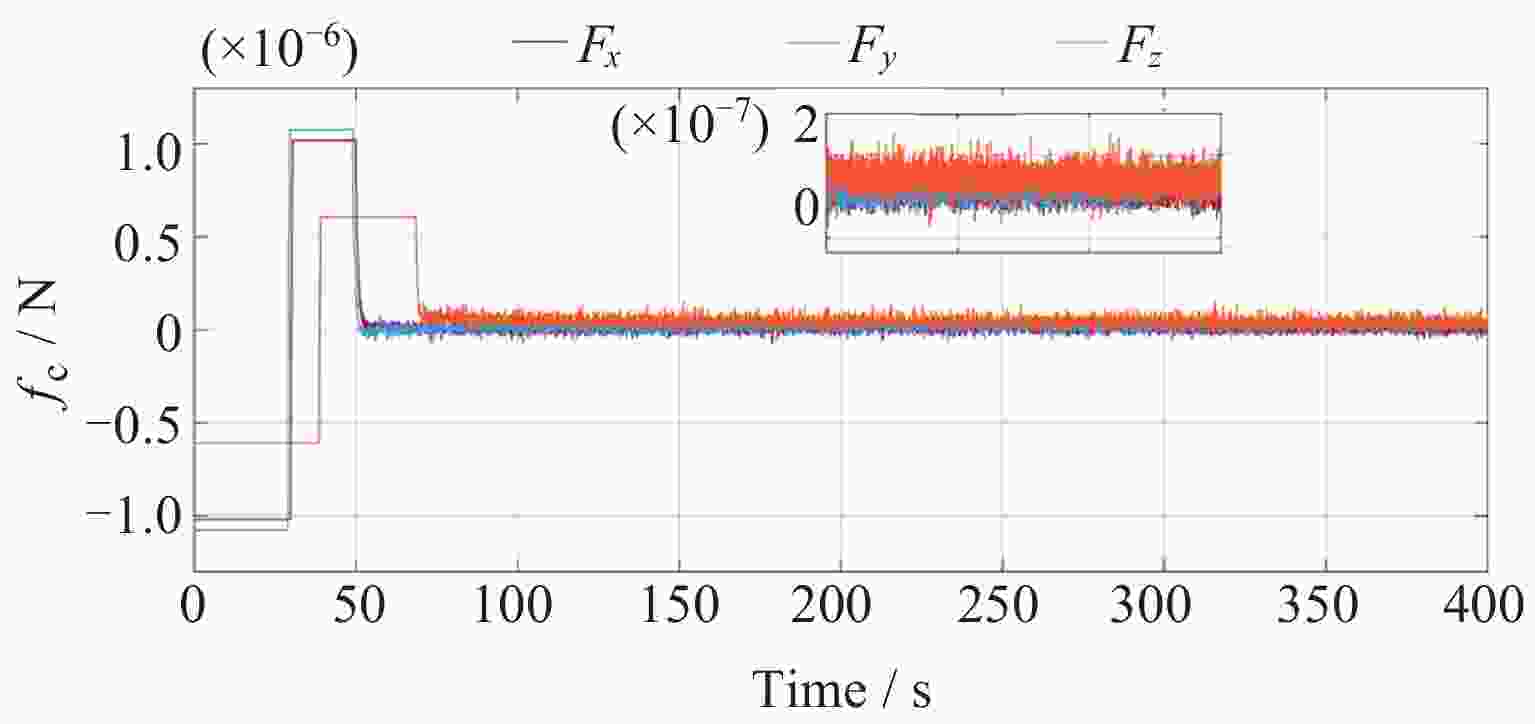
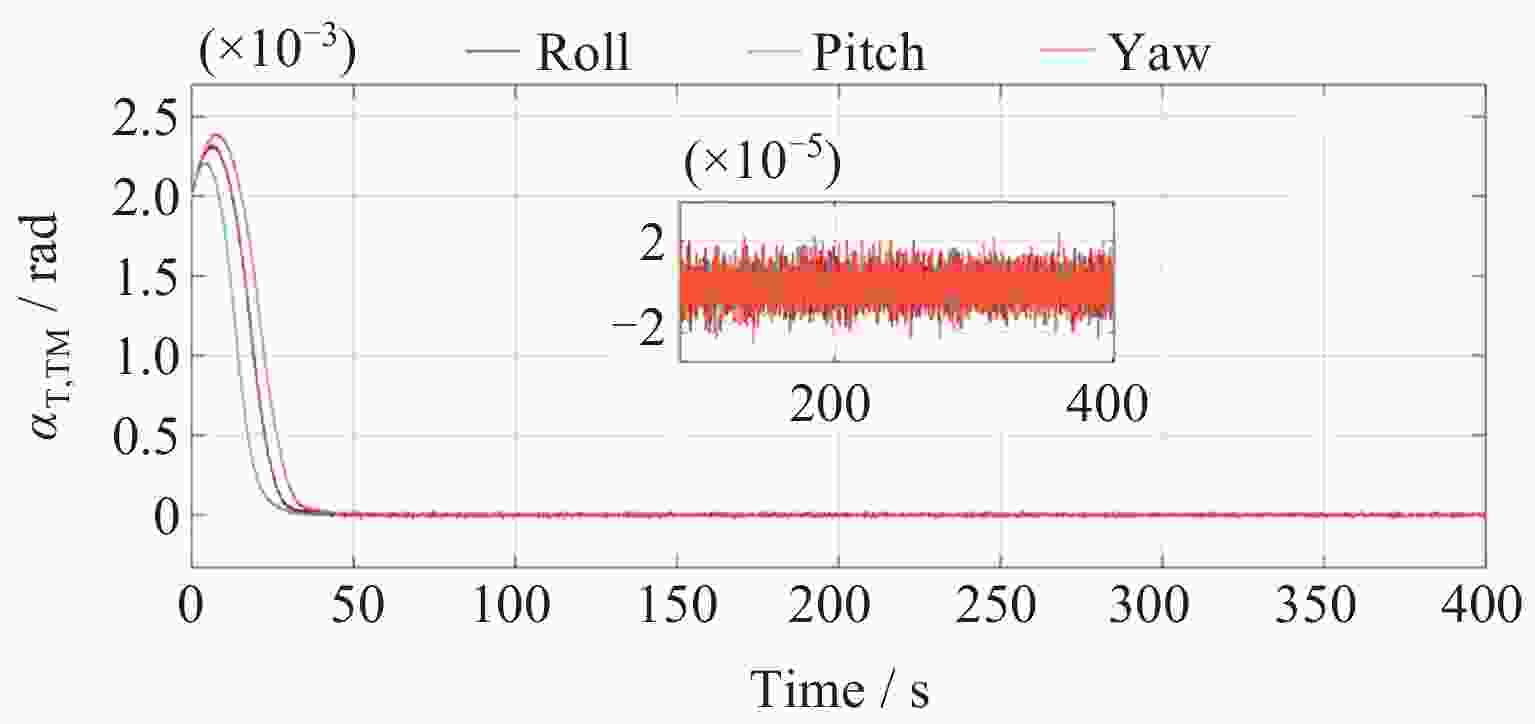
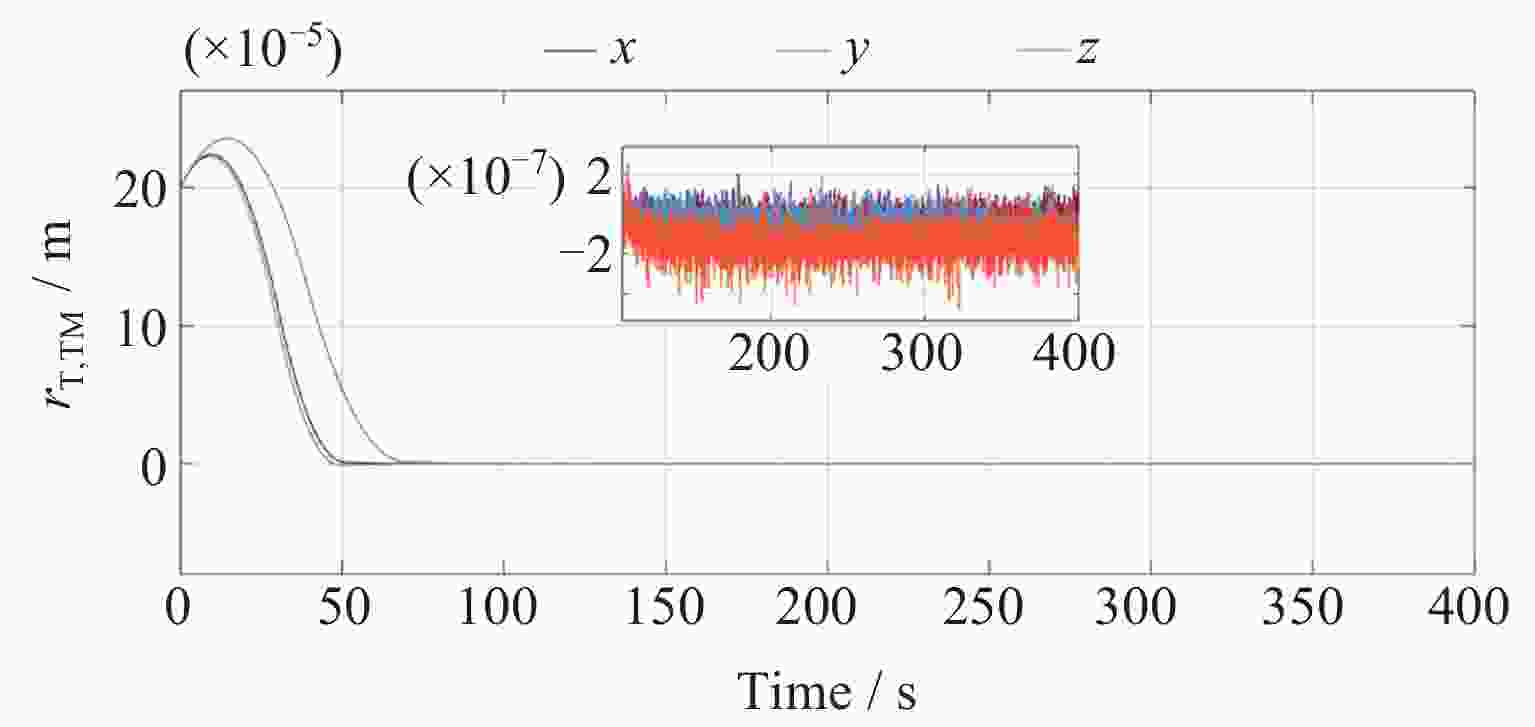
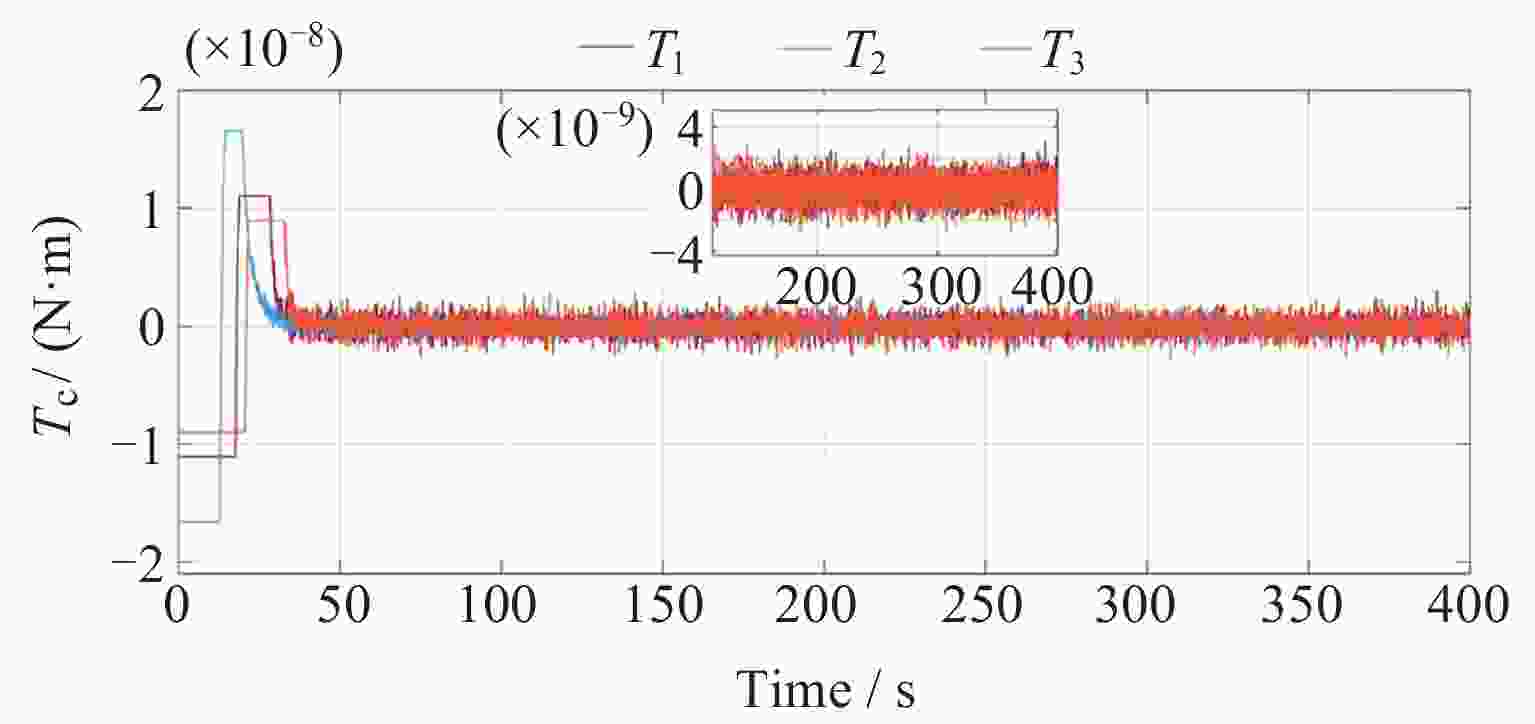
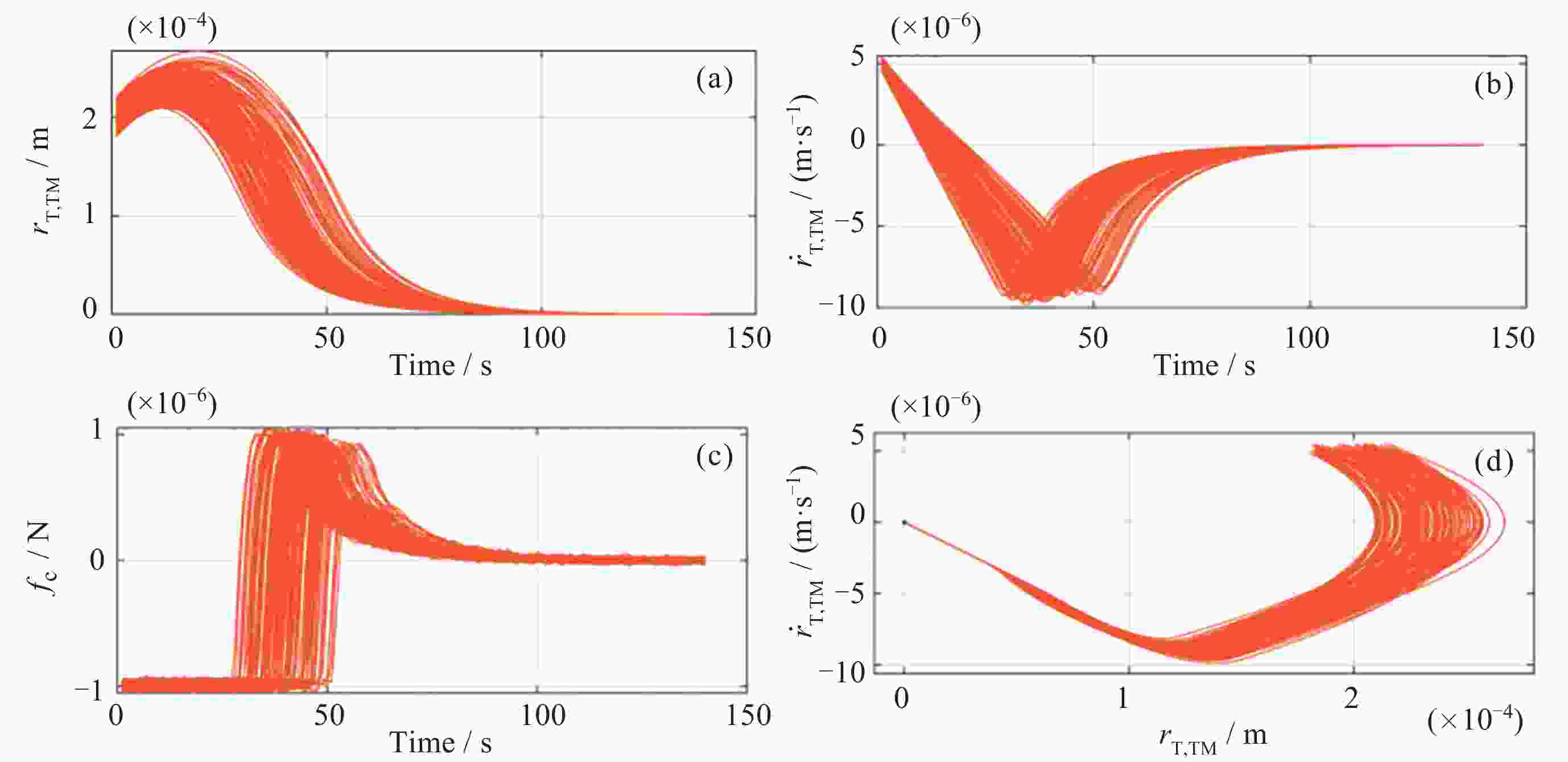
Abstract: In the space-borne gravitational wave detection missions, test mass capture is critical for the spacecraft to enter the super-stable flight state. This process is characterized by large initial errors, large system uncertainties and strong execution constraints. This paper presents an improved high precision elastic tube model predictive control of test mass capture. A control structure based on rolling optimization and elastic tube technology is proposed to improve the capture success rate and effectively compensate the satellite coupling interference on test mass. The tiny tolerance active set method is proposed to improve the accuracy of online calculation and ensure the high control accuracy of test mass. Meanwhile, this paper proposes an offline correction method for the minimum robust positive invariant set based on feature engineering. It reduces the vertices of the minimum robust positive invariant set based on the Minkowski summation and reduces the online computational complexity. The proposed method is verified by simulations on the space-based double test masses full-freedom simulation platform. The results show that the control performance satisfies the test mass capture accuracy requirement. The controller is robust and the rate of convergence is improved effectively. The effects of platform motion interference and measurement noise are suppressed. -
图 6 不同容差$ \varepsilon $和$ \epsilon $下检验质量捕获量测信号的对比
Figure 6. Comparison of test mass capture measurement signals with different tolerances $ \varepsilon $ and $ \epsilon $
图 7 不同容差$ \varepsilon $和$ \epsilon $下检验质量捕获控制信号的对比
Figure 7. Comparison of test mass capture control signals with different tolerances $ \varepsilon $ and $ \epsilon $
图 21 检验质量相对位移鲁棒性验证
Figure 21. Test mass robustness verification of relative displacement
表 1 优化问题简化前后空间复杂度对比
Table 1. Comparison of spatial complexity before and after simplification of optimization problems
简化前维度 简化后维度 $ {e}_{N} $ 59$ N $+58=3008 19$ N $+18=968 $ {Q}_{{t}} $ (59$ N $+58)$ \times $(59$ N $+58)=
3008$ \times $3008(19$ N $+18)$ \times $(19$ N $+18)=
968$ \times $968$ {P}_{{t}} $ 59$ N $+58=3008 19$ N $+18=968 $ {A}_{{i}} $ (118$ N $+118)$ \times $(59$ N $+58)=
6018$ \times $3008(38$ N $+38)$ \times $(19$ N $+18)=
1938$ \times $968
下载: 导出CSV
表 2 检验质量释放初始状态和控制误差要求
Table 2. Test mass release initial states and control error requirements
检验质量状态 初始状态 控制误差 线位移 $ \pm 200$ μm $ < 25 $ μm 线速度 $ \pm 5\times {10}^{-6} $ m·s–1 $ < 1\times {10}^{-6} $ m·s–1 角位移 $ \pm 2\;\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d} $ $ < 100 $ μrad 角速度 $ \pm 1\times {10}^{-4} $ rad·s–1 $ < 1\times {10}^{-5} $ rad·s–1
下载: 导出CSV
表 3 随机噪声幅值
Table 3. Random noise amplitudes
自由度 执行器噪声幅值 量测噪声幅值 x $ < 4.35\times {10}^{-14}\; \mathrm{N} $ $ < 2.24\times {10}^{-7}\; \mathrm{m} $ y $ < 4.41\times {10}^{-13}\; \mathrm{N} $ $ < 2.38\times {10}^{-7}\; \mathrm{m} $ z $ < 4.68\times {10}^{-13}\; \mathrm{N} $ $ < 3.82\times {10}^{-7}\; \mathrm{m} $ $ \varphi $ $ < 4.11\times {10}^{-15}\; \mathrm{N}·\mathrm{m} $ $ < 2.45\times {10}^{-5}\; \mathrm{r}\mathrm{a}\mathrm{d} $ $ \theta $ $ < 4.43\times {10}^{-15}\; \mathrm{N}·\mathrm{m} $ $ < 1.59\times {10}^{-5}\; \mathrm{r}\mathrm{a}\mathrm{d} $ $ \psi $ $ < 4.38\times {10}^{-15}\; \mathrm{N}·\mathrm{m} $ $ < 2.50\times {10}^{-5}\; \mathrm{r}\mathrm{a}\mathrm{d} $
下载: 导出CSV
表 4 执行器饱和
Table 4. Actuator saturation constraints
自由度 控制力饱和/N 自由度 控制力矩饱和/(N·m) $ {f}_{x} $ $ 1.019\times {10}^{-6} $ $ {T}_{\mathrm{r}\mathrm{o}\mathrm{l}\mathrm{l}} $ 1.1$ 00\times {10}^{-8} $ $ {f}_{y} $ $ 1.078\times {10}^{-6} $ $ {T}_{\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}} $ 1.66$ 0\times {10}^{-8} $ $ {f}_{z} $ $ 6.076\times {10}^{-7} $ $ {T}_{\mathrm{y}\mathrm{a}\mathrm{w}} $ $ 8.990\times {10}^{-9} $
下载: 导出CSV
表 5 MPC算法控制器参数
Table 5. MPC algorithm controller parameters
x y z $ \varphi $ $ \theta $ $ \psi $ 位移 1 1 1 1 1 1 速度 5 5 10 10 5 10 控制 10 10 10 10 10 10
下载: 导出CSV
表 6 ETMPC位移权重
Table 6. ETMPC displacement weight
x y z $ {\boldsymbol{Q}}_{z} $ $ \left[\begin{array}{cc}1& 0\\ 0& 100\end{array}\right] $ $ \left[\begin{array}{cc}1& 0\\ 0& 90\end{array}\right] $ $ \left[\begin{array}{cc}1& 0\\ 0& 230\end{array}\right] $ $ {Q}_{v} $ 30 30 30
下载: 导出CSV
表 7 ETMPC姿态权重
Table 7. ETMPC pose weight
$ \varphi $ $ \theta $ $ \psi $ $ {\boldsymbol{Q}}_{z} $ $ \left[\begin{array}{cc}1& 0\\ 0& 30\end{array}\right] $ $ \left[\begin{array}{cc}1& 0\\ 0& 20\end{array}\right] $ $ \left[\begin{array}{cc}1& 0\\ 0& 400\end{array}\right] $ $ {Q}_{v} $ 30 30 30
下载: 导出CSV
表 8 平均调节时间对比
Table 8. Average adjustment time comparison
算法 平均调节时间$ {t}_{\mathrm{s}} $/s 位置 SMC 77.8 MPC 65.3 ETMPC 51.5 姿态 SMC 72.3 MPC 68.3 ETMPC 29.8
下载: 导出CSV
表 9 仿真参数变化范围
Table 9. Variation range of simulation parameters
参数 取值范围 刚度系数/$ {\mathrm{s}}^{-2} $ [$ 5\times {10}^{-5},\;5\times {10}^{-4} $] 初始位置/$ \mathrm{m} $ [$ 1.8\times {10}^{-4},\;2.2\times {10}^{-4} $] 初始线速度/($ \mathrm{m}\cdot {\mathrm{s}}^{-1} $) [$ 4.5\times {10}^{-6},\;5.5\times {10}^{-6} $]
下载: 导出CSV
-
[1] SCHLEICHER A, ZIEGLER T, SCHUBERT R, et al. In-orbit performance of the LISA Pathfinder drag-free and attitude control system[J]. CEAS Space Journal, 2018, 10(4): 471-485 doi: 10.1007/s12567-018-0204-x [2] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测“太极计划”及“太极1号”在轨测试[J]. 深空探测学报, 2020, 7(1): 3-10LUO Ziren, ZHANG Min, JIN Gang, et al. Introduction of Chinese space-borne gravitational wave detection program “Taiji” and “Taiji-1” satellite mission[J]. Journal of Deep Space Exploration, 2020, 7(1): 3-10 [3] 罗俊, 艾凌皓, 艾艳丽, 等. 天琴计划简介[J]. 中山大学学报(自然科学版), 2021, 60(1/2): 1-19LUO Jun, AI Linghao, AI Yanli, et al. A brief introduction to the TianQin project[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2021, 60(1/2): 1-19 [4] 李洪银, 叶小容, 刘佳恒, 等. 天琴无拖曳控制研究的关键问题[J]. 中山大学学报(自然科学版), 2021, 60(1/2): 213-224LI Hongyin, YE Xiaorong, LIU Jiaheng, et al. Key issues in the research on drag-free control for TianQin[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2021, 60(1/2): 213-224 [5] LIAN X B, ZHANG J X, YANG J K, et al. The determination for ideal release point of test masses in drag-free satellites for the detection of gravitational waves[J]. Advances in Space Research, 2021, 67(2): 824-833 doi: 10.1016/j.asr.2020.09.030 [6] LIAN X B, ZHANG J X, CHANG L T, et al. Test mass capture for drag-free satellite based on RBF neural network adaptive sliding mode control[J]. Advances in Space Research, 2022, 69(2): 1205-1219 doi: 10.1016/j.asr.2021.10.009 [7] VIDANO S, NOVARA C, PAGONE M, et al. The LISA DFACS: model predictive control design for the test mass release phase[J]. Acta Astronautica, 2022, 193: 731-743 doi: 10.1016/j.actaastro.2021.12.056 [8] LIU Y X, LI Y, WANG P C, et al. Constrained nonlinear high-efficiency model predictive technics for test mass capture[J]. Advances in Space Research, 2023, 72(2): 180-199 doi: 10.1016/j.asr.2023.02.046 [9] TSAI Y K, MALAK R J. Robust control co-design using tube-based model predictive control[C]//2023 American Control Conference (ACC). San Diego: IEEE, 2023: 769-775 [10] 邹恒光, 宋继良, 王军政, 等. 卫星编队的管道模型预测控制方法研究[J]. 北京理工大学学报, 2021, 41(2): 201-206ZOU Hengguang, SONG Jiliang, WANG Junzheng, et al. Satellite formation control strategy with Tube-based MPC[J]. Transactions of Beijing Institute of Technology, 2021, 41(2): 201-206 [11] 管萍, 吴希岩, 戈新生. 基于Tube的挠性航天器模型预测姿态控制及主动振动控制[J]. 振动与冲击, 2022, 41(16): 261-270GUAN Ping, WU Xiyan, GE Xinsheng. Tube-based model predictive attitude control and active vibration control for flexible spacecraft[J]. Journal of Vibration and Shock, 2022, 41(16): 261-270 [12] RAKOVIĆ S V, LEVINE W S, AÇIKMESE B. Elastic tube model predictive control[C]//2016 American Control Conference (ACC). Boston: IEEE, 2016: 3594-3599 [13] RAKOVIC S V, KERRIGAN E C, KOURAMAS K I, et al. Invariant approximations of the minimal robust positively invariant set[J]. IEEE Transactions on Automatic Control, 2005, 50(3): 406-410 doi: 10.1109/TAC.2005.843854 [14] VIDANO S, NOVARA C, COLANGELO L, et al. The LISA DFACS: A nonlinear model for the spacecraft dynamics[J]. Aerospace Science and Technology, 2020, 107: 106313 doi: 10.1016/j.ast.2020.106313 [15] BASILE F. Modeling and Design for the Attitude Control Phase of the LISA Drag-free Mission[D]. Torino: Politecnico di Torino, 2019 [16] Multi-Parametric Toolbox 3[DB/MT]. (2019-02-02)[2024-01-08]. https://www.mpt3.org/ [17] TROBBIANI L. Alternative Control Strategy for Test Mass Release of Spaceborne Inertial Sensors[D]. Pisa: Università di Pisa, 2014 -
-
下载:
计量
- 文章访问数: 369
- HTML全文浏览量: 217
- PDF下载量: 37
-
被引次数:
0(来源:Crossref)
0(来源:其他)
