基于极限学习机的地磁模型误差预测方法

郭红阳; 张涛; 韩鹏; 陈晨; 赵治华

doi:10.11728/cjss2025.05.2024-0109

基于极限学习机的地磁模型误差预测方法

doi: 10.11728/cjss2025.05.2024-0109 cstr: 32142.14.cjss.2024-0109

郭红阳^1,,
张涛¹,
韩鹏²,
陈晨¹,
赵治华^1,

1.
河南工业大学机电工程学院　郑州　450001
2.
中国科学院国家空间科学中心　北京　100190

基金项目: 河南省科技厅自然科学项目资助(242102221043)

详细信息

作者简介:

郭红阳　男, 2001年3月出生于河南省洛阳市, 2022年于辽宁工程技术大学获得学士学位. 目前于河南工业大学机电工程学院就读硕士研究生, 主要研究方向自主导航, 人工智能. E-mail: 13837955150@163.com

赵治华　男, 1987年8月出生于河南省新县, 现为河南工业大学机电工程学院副教授, 硕士生导师, 主要研究方向为智能传感器制备及其中粮油食品品质监测、疾病无创断等领域的应用. E-mail: zhaozhihua@haut.edu.cn

中图分类号: V249.3
计量
- 文章访问数: 105
- HTML全文浏览量: 12
- PDF下载量: 6
- 被引次数:
  0(来源:Crossref)
  
  0(来源:其他)
出版历程
- 收稿日期: 2024-08-30
- 修回日期: 2025-05-07
- 网络出版日期: 2025-05-09

Error Prediction Method of Geomagnetic Model Based on Extreme Learning Machine

1.
School of Mechanical and Electrical Engineering, Henan University of Technology, Zhengzhou 450001
2.
National Space Science Center, Chinese Academy of Sciences, Beijing 100190

摘要

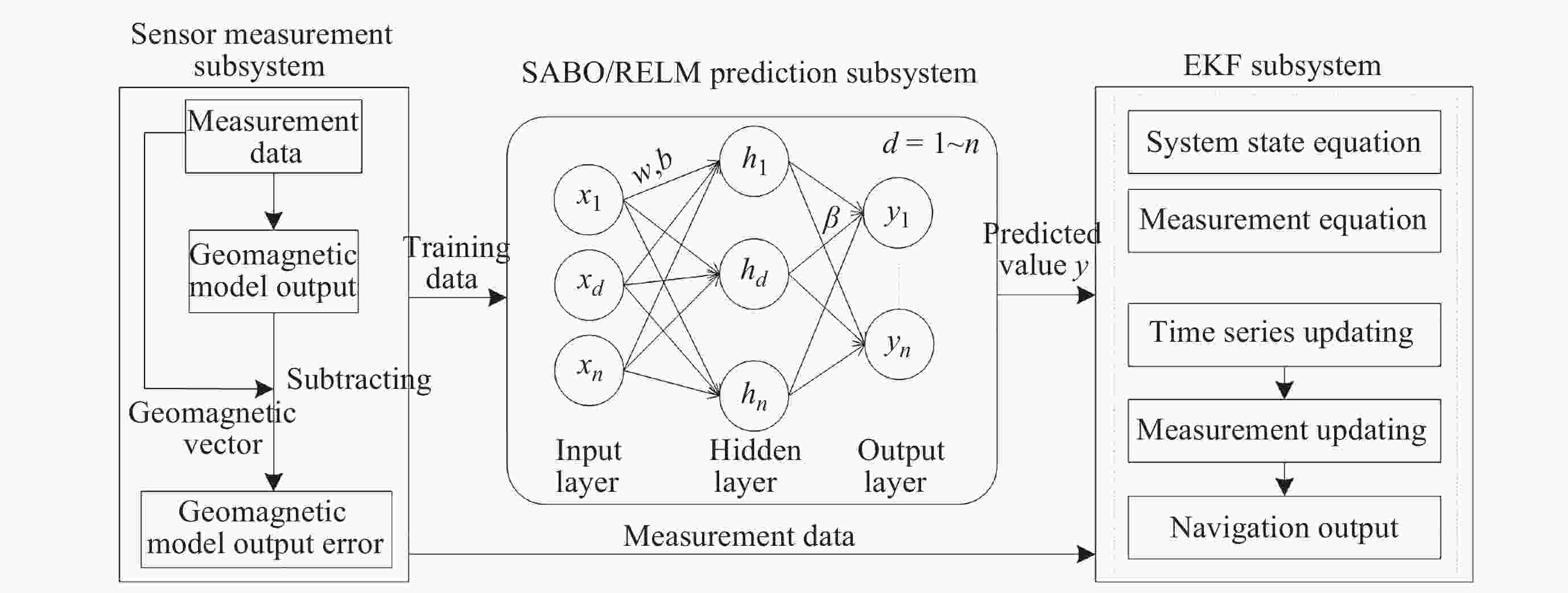
摘要: 高精度地磁场模型是近地卫星自主导航的重要基础, 但地磁模型因观测误差、球谐系数截断误差及更新缓慢等原因制约了导航精度的提高. 为了解决这个问题, 基于正则化极限学习机提出一种地磁模型误差预测方法, 采用减法均值器对正则化系数C进行最优估计, 减少了参数调试中的主观性和随机性, 提高了学习的效率和预测的精度, 另外该方法可以有效提高地磁观测序列中存在野值时误差估计精度; 与滤波算法进行融合, 提出一种模型误差补偿的地磁导航方法, 并利用在轨卫星真实的地磁测量数据进行了仿真验证. 结果表明, 所提出方法的预测精度优于常用的几种神经网络预测方法, 导航精度达到了1.26 km, 表明所提出的误差预测模型可以有效地改善地磁导航性能.
- 极限学习机 /
- 正则化 /
- 减法均值器 /
- 地磁滤波
Abstract: The high-precision geomagnetic field model is an important foundation for autonomous navigation of near earth satellites, but the improvement of navigation accuracy is constrained by observation errors, spherical harmonic truncation errors, and slow updates of the geomagnetic model. To solve this problem, this paper proposes a geomagnetic model error prediction method based on regularized extreme learning machine. The optimal estimation of the regularization coefficient C is achieved by using a subtraction mean algorithm, which reduces subjectivity and randomness in parameter tuning, improves learning efficiency and prediction accuracy. In addition, this method can effectively improve the error estimation accuracy when outliers exist in geomagnetic observation sequences. Then, a geomagnetic navigation method with model error compensation was proposed by integrating it with filtering algorithms, and simulation verification was conducted using real geomagnetic measurement data from in orbit satellites. The results show that the prediction accuracy of the method proposed in this paper is superior to several commonly used neural network prediction methods, and the navigation accuracy reaches 1.49km, indicating that the proposed error prediction model can effectively improve the performance of geomagnetic navigation.
- Extreme learning machine /
- Regularization /
- Subtraction mean /
- Geomagnetic filter
注释:

1) 1http://swarm-diss.eo.esa.int

HTML全文

图 1 2024年和2020年误差数据信息对比. (a)三个分量的地磁模型误差, (b)位置误差滤波过程

Figure 1. Comparison of error data information in 2024 and 2020. (a)Error diagram of geomagnetic model with three components, (b) position error filtering process diagram

下载: 全尺寸图片幻灯片

图 2 SABO/RELMEKF导航方法的系统模型框架

Figure 2. System model framework of SABO/RELMEKF navigation method

下载: 全尺寸图片幻灯片

图 3 SABO/RELM模型误差预测与地磁模型实际误差对比

Figure 3. Comparison between the predicted value and the actual value of SABO/RELM model

下载: 全尺寸图片幻灯片

图 4 B_y方向地磁模型实际误差波动较大区域统计

Figure 4. Statistical analysis of areas with significant fluctuations in actual errors of the B_y-direction geomagnetic model

下载: 全尺寸图片幻灯片

图 5 总磁场强度F标量误差对比. (a) ELM的预测效果(含异常值), (b) SABO/RELM的预测效果(含异常值)

Figure 5. Comparison of total magnetic field intensity F scalar error. (a) ELM (including outliers), (b) SABO/RELM (including outliers)

下载: 全尺寸图片幻灯片

图 6 位置估计误差

Figure 6. Position estimation error when the sampling interval of measurement data

下载: 全尺寸图片幻灯片

表 1 2020年和2024年地磁模型误差对比

Table 1. Comparison of geomagnetic field errors in 2020 and 2024

日期	B_x		B_y		B_z		P_error
日期	均值/nT	标准差	均值/nT	标准差	均值/nT	标准差	误差/km
2020年1月	68.72	46.90	–0.83	24.01	–5.29	39.81	7.16
2024年1月	82.91	58.17	–2.28	51.56	–6.30	45.52	10.47

下载: 导出CSV

表 2 地磁模型实际误差与修正后的地磁模型误差对比

Table 2. Statistical comparison of actual model error and prediction error

地磁矢量	地磁模型实际误差		修正后模型误差		优化比例
地磁矢量	均值/nT	标准差	均值/nT	标准差	均值/(%)	标准差/(%)
B_x	–77.61	46.90	–2.40	28.11	96.91	40.06
B_y	2.64	35.56	1.03	28.56	60.98	19.69
B_z	7.49	39.06	–1.01	17.56	86.52	55.04

下载: 导出CSV

表 3 神经网络预测结果的误差统计

Table 3. Error statistics of neural network prediction results

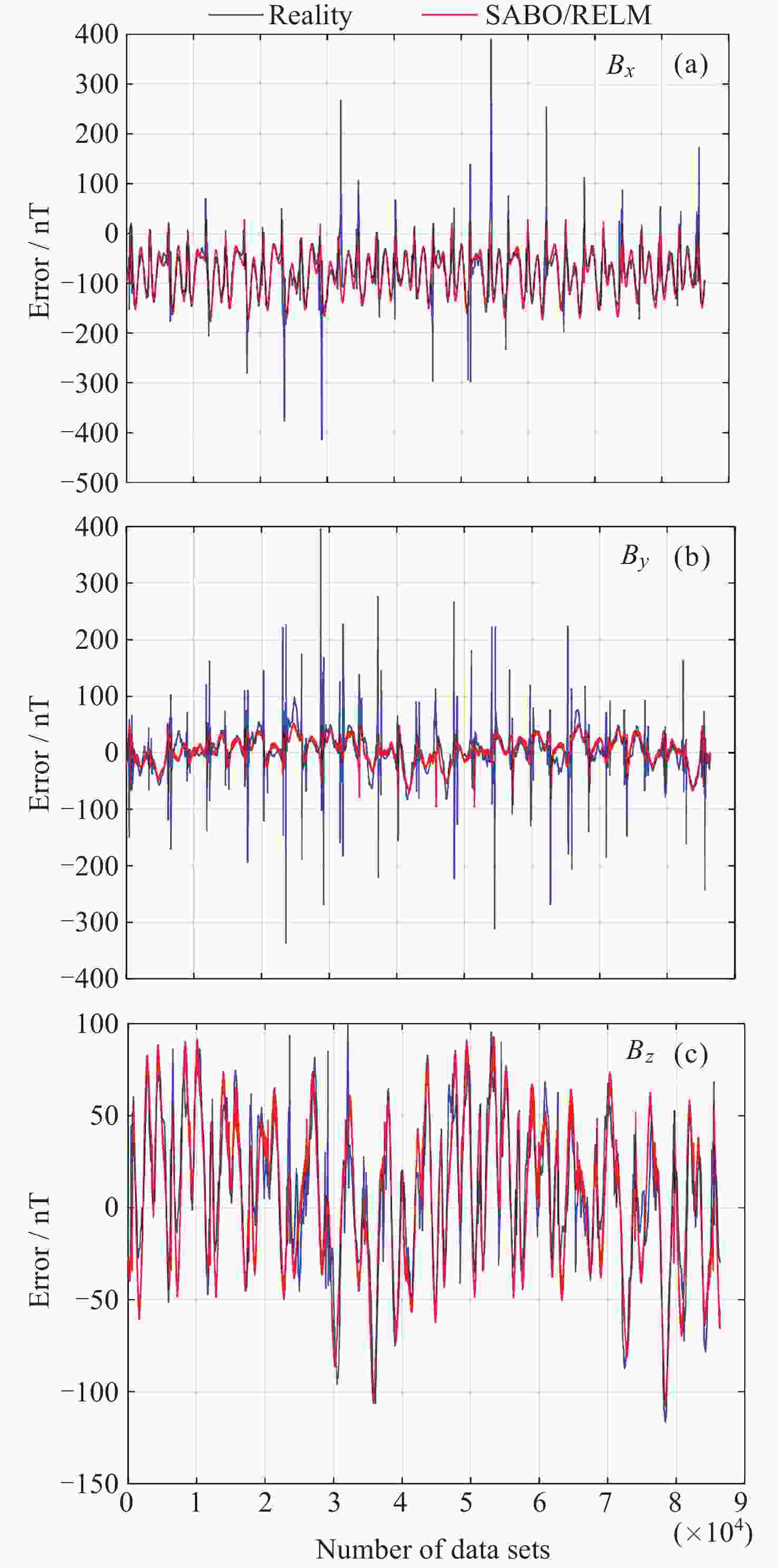
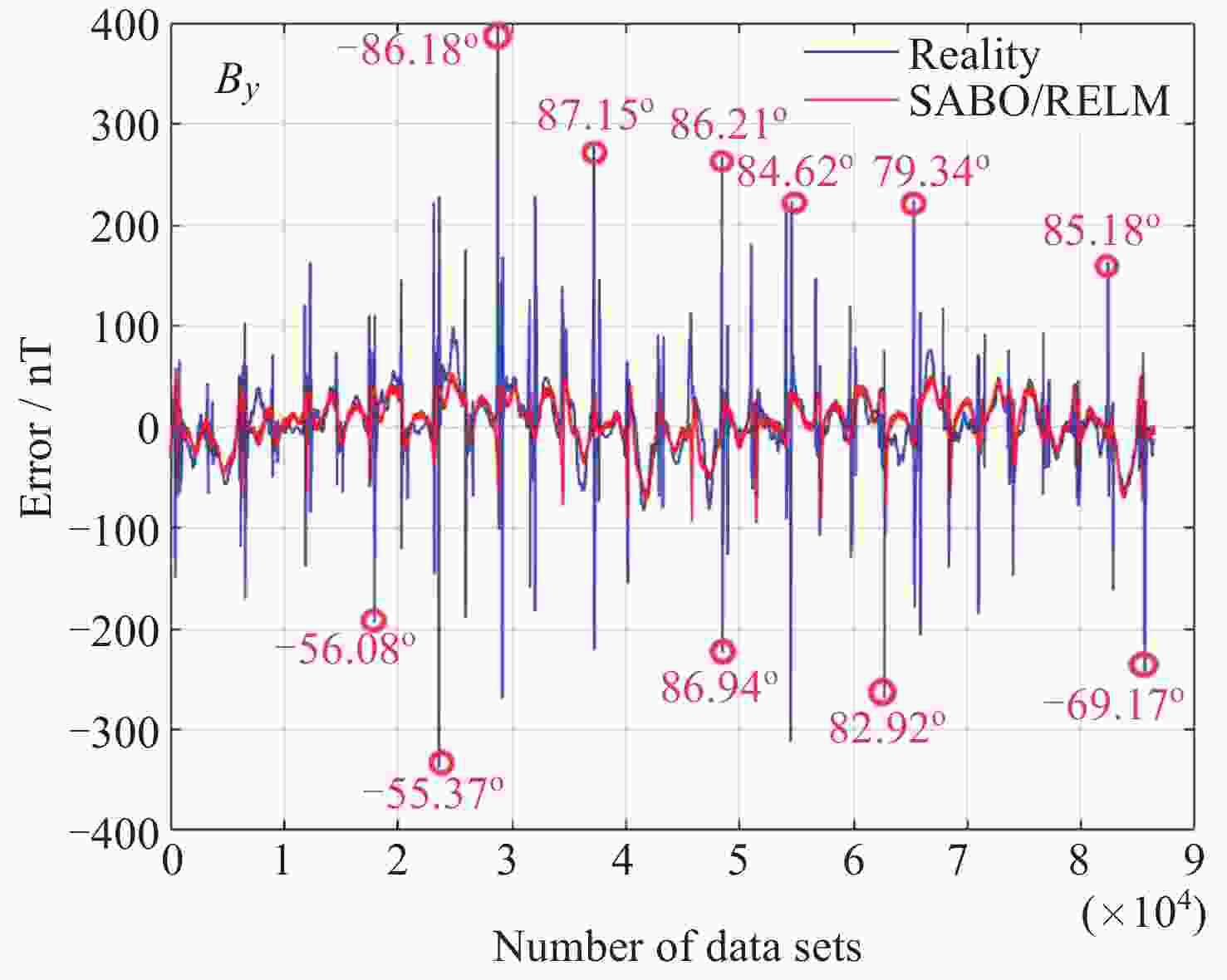
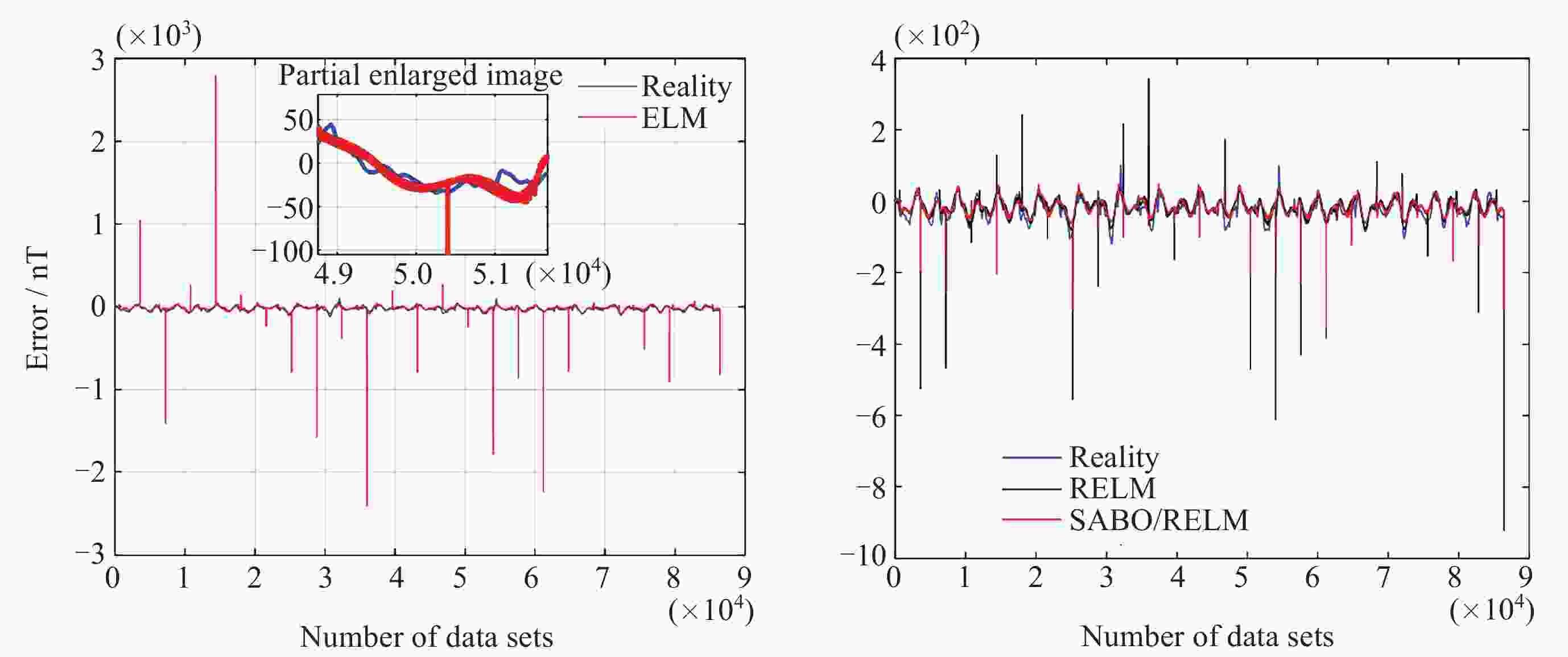
方法	B_x		B_y		B_z
方法	均值/nT	标准差	均值/nT	标准差	均值/nT	标准差
ELM(不含异常值)	–80.01	40.91	3.68	23.34	6.48	40.45
ELM(含异常值)	–80.28	52.26	4.19	53.42	6.40	57.04
RELM(含异常值)	–79.61	37.94	3.56	18.77	6.78	36.82
SABO/RELM(含异常值)	–79.70	40.59	3.67	21.83	6.75	39.31

下载: 导出CSV

表 4 地磁导航方法的误差统计

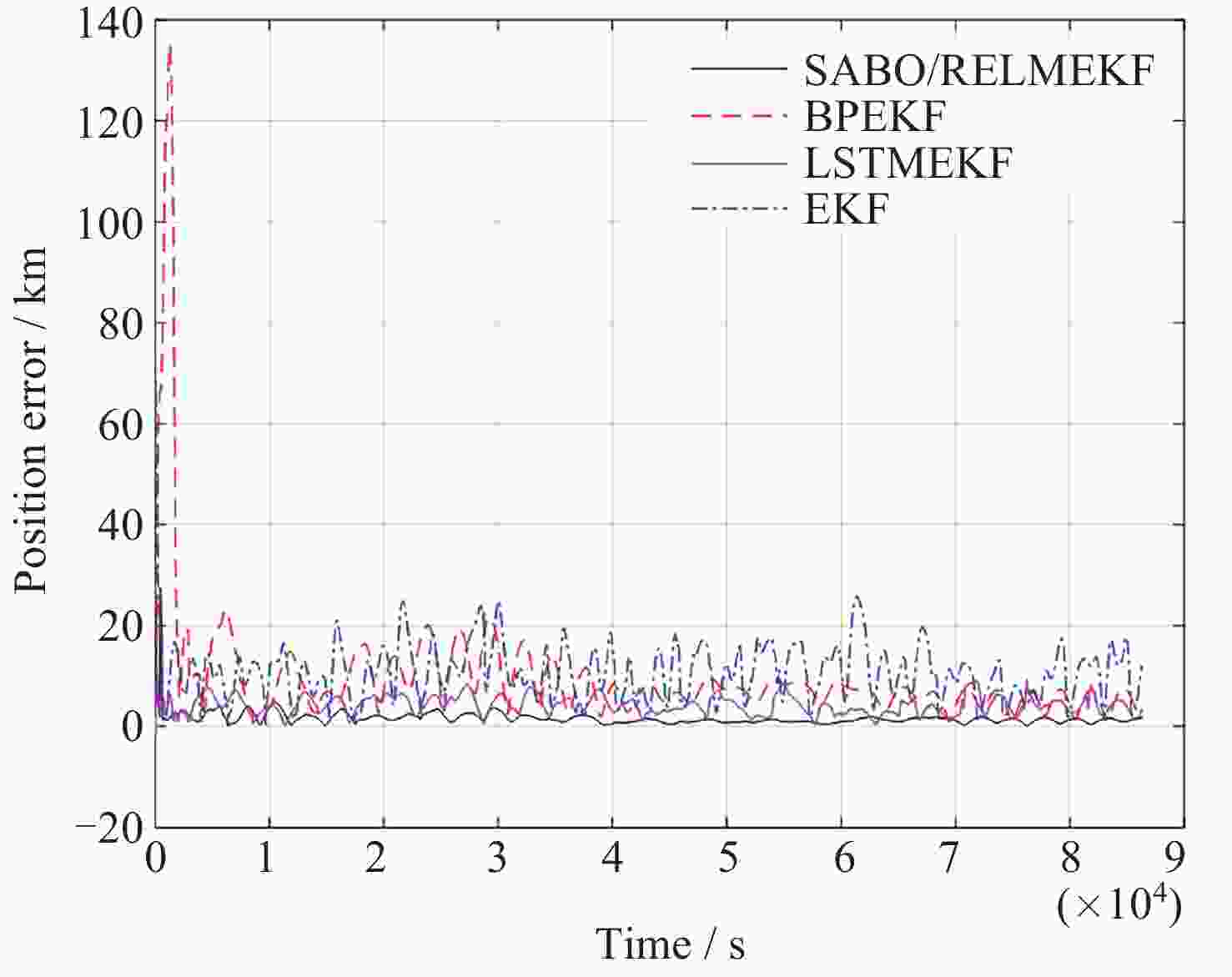
Table 4. Comparison of error statistics of multiple filter navigation

导航方法	位置误差/km	速度误差/(m·s^–1)
SABO/RELM	1.26	1.39
BP	5.17	5.70
LSTM	3.75	4.08
EKF	11.54	12.21

下载: 导出CSV

参考文献(19)

[1]	CHEN G F, YU F, ZONG H, et al. Geomagnetic orbit determination using fuzzy regulating unscented Kalman filter[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2021, 38(4): 695-703
[2]	KIANI M, POURTAKDOUST S H. Adaptive square-root cubature–quadrature Kalman particle filter via KLD-sampling for orbit determination[J]. Aerospace Science and Technology, 2015, 46: 159-167 doi: 10.1016/j.ast.2015.07.008
[3]	LI X, SONG B Q, WANG Y J, et al. Calibration and alignment of tri-axial magnetometers for attitude determination[J]. IEEE Sensors Journal, 2018, 18(18): 7399-7406 doi: 10.1109/JSEN.2018.2859832
[4]	向奉卓, 李广云, 王力, 等. 基于递推最小二乘的三轴磁强计在线自校正方法[J]. 传感器与微系统, 2019, 38(2): 30-33 XIANG Fengzhuo, LI Guangyun, WANG Li, et al. Three-axis magnetometer online self-calibration method based on recursive least square[J]. Transducer and Microsystems Technologies, 2019, 38(2): 30-33
[5]	BAI W Q, ZHANG X H, ZHANG S L, et al. Long-distance geomagnetic navigation in GNSS-denied environments with deep reinforcement learning[OL]. arXiv preprint arXiv: 2410.15837, 2024
[6]	CHEN Z, LIU K J, ZHANG Q, et al. Geomagnetic vector pattern recognition navigation method based on probabilistic neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5909608
[7]	WINTOFT P, WIK M. Exploring three recurrent neural network architectures for geomagnetic predictions[J]. Frontiers in Astronomy and Space Sciences, 2021, 8: 664483 doi: 10.3389/fspas.2021.664483
[8]	何欣燃, 钟秋珍, 崔延美, 等. 基于长短期记忆神经网络的太阳耀斑短期预报[J]. 空间科学学报, 2022, 42(5): 862-872 doi: 10.11728/cjss2022.05.210315028 HE Xinran, ZHONG Qiuzhen, CUI Yanmei, et al. Solar flare short-term forecast model based on long and short-term memory neural network[J]. Chinese Journal of Space Science, 2022, 42(5): 862-872 doi: 10.11728/cjss2022.05.210315028
[9]	SICILIANO F, CONSOLINI G, TOZZI R, et al. Forecasting SYM‐H index: a comparison between long short‐term memory and convolutional neural networks[J]. Space Weather, 2020, 19(2): e2020SW002589
[10]	TASISTRO-HART A, GRAYVER A, KUVSHINOV A. Probabilistic geomagnetic storm forecasting via deep learning[J]. Journal of Geophysical Research: Space Physics, 2021, 126(1): e2020JA028228 doi: 10.1029/2020JA028228
[11]	杨茂, 张书天, 王勃. 基于因果正则化极限学习机的风电功率短期预测方法[J]. 电力系统保护与控制, 2024, 52(11): 127-136 YANG Mao, ZHANG Shutian, WANG Bo. Short-term wind power forecasting method based on a causal regularized extreme learning machine[J]. Power System Protection and Control, 2024, 52(11): 127-136
[12]	WANG H, XU L W, TAO Y, et al. OP performance prediction for complex mobile multiuser networks based on extreme learning machine[J]. IEEE Access, 2020, 8: 14557-14564 doi: 10.1109/ACCESS.2020.2966690
[13]	TROJOVSKY P, MOHAMMAD D. Subtraction-average-based optimizer: a new swarm-inspired metaheuristic algorithm for solving optimization problems[J]. Biomimetics, 2023, 8(2): 149 doi: 10.3390/biomimetics8020149
[14]	ALKEN P, THÉBAULT E, BEGGAN C D, et al. International geomagnetic reference field: the thirteenth generation[J]. Earth, Planets and Space, 2021, 73: 49 doi: 10.1186/s40623-020-01288-x
[15]	张涛, 张文博, 高东, 等. 一种神经网络预测模型误差的地磁导航方法[J]. 航天控制, 2024, 42(1): 37-42 doi: 10.3969/j.issn.1006-3242.2024.01.006 ZHANG Tao, ZHANG Wenbo, GAO Dong, et al. A geomagnetic navigation method based on neural network prediction model error[J]. Aerospace Control, 2024, 42(1): 37-42 doi: 10.3969/j.issn.1006-3242.2024.01.006
[16]	WINCH D E, IVERS D J, TURNER J P R, et al. Geomagnetism and Schmidt quasi-normalization[J]. Geophysical Journal International, 2005, 160(2): 487-504 doi: 10.1111/j.1365-246X.2004.02472.x
[17]	高东, 朱明慧, 韩鹏. 一种地磁/惯性深度融合导航方法[J]. 中国惯性技术学报, 2022, 30(4): 437-444 GAO Dong, ZHU Minghui, HAN Peng. A geomagnetic/inertial depth fusion navigation method[J]. Journal of Chinese Inertial Technology, 2022, 30(4): 437-444
[18]	JIAO M, WANG D Q, YANG Y, et al. More intelligent and robust estimation of battery state-of-charge with an improved regularized extreme learning machine[J]. Engineering Applications of Artificial Intelligence, 2021, 104: 104407 doi: 10.1016/j.engappai.2021.104407
[19]	卢兆兴, 吕志峰, 李婷, 等. 基于BP神经网络的地磁变化场预测研究[J]. 大地测量与地球动力学, 2021, 41(3): 229-233 LU Zhaoxing, LÜ Zhifeng, LI Ting, et al. Forecasting of the variable geomagnetic field based on BP neural network[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 229-233