小天体动能撞击防御中动量传递因子敏感参数分析
doi: 10.11728/cjss2022.03.210126013 cstr: 32142.14.cjss2022.03.210126013
Analysis of Sensitive Parameters of Momentum Transfer Factor in Kinetic Impact Defending Small Bodies
-
摘要: 动量传递因子
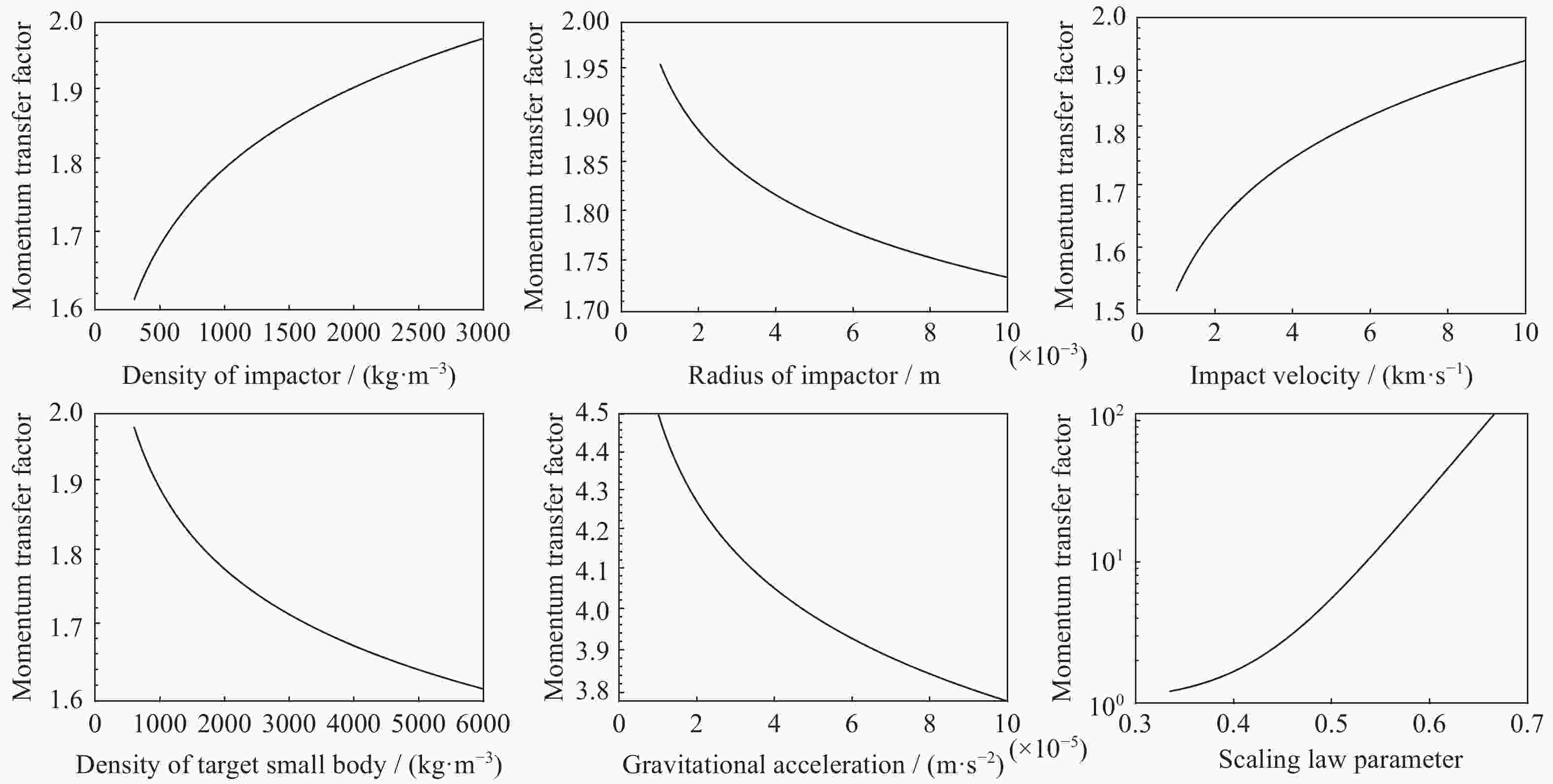
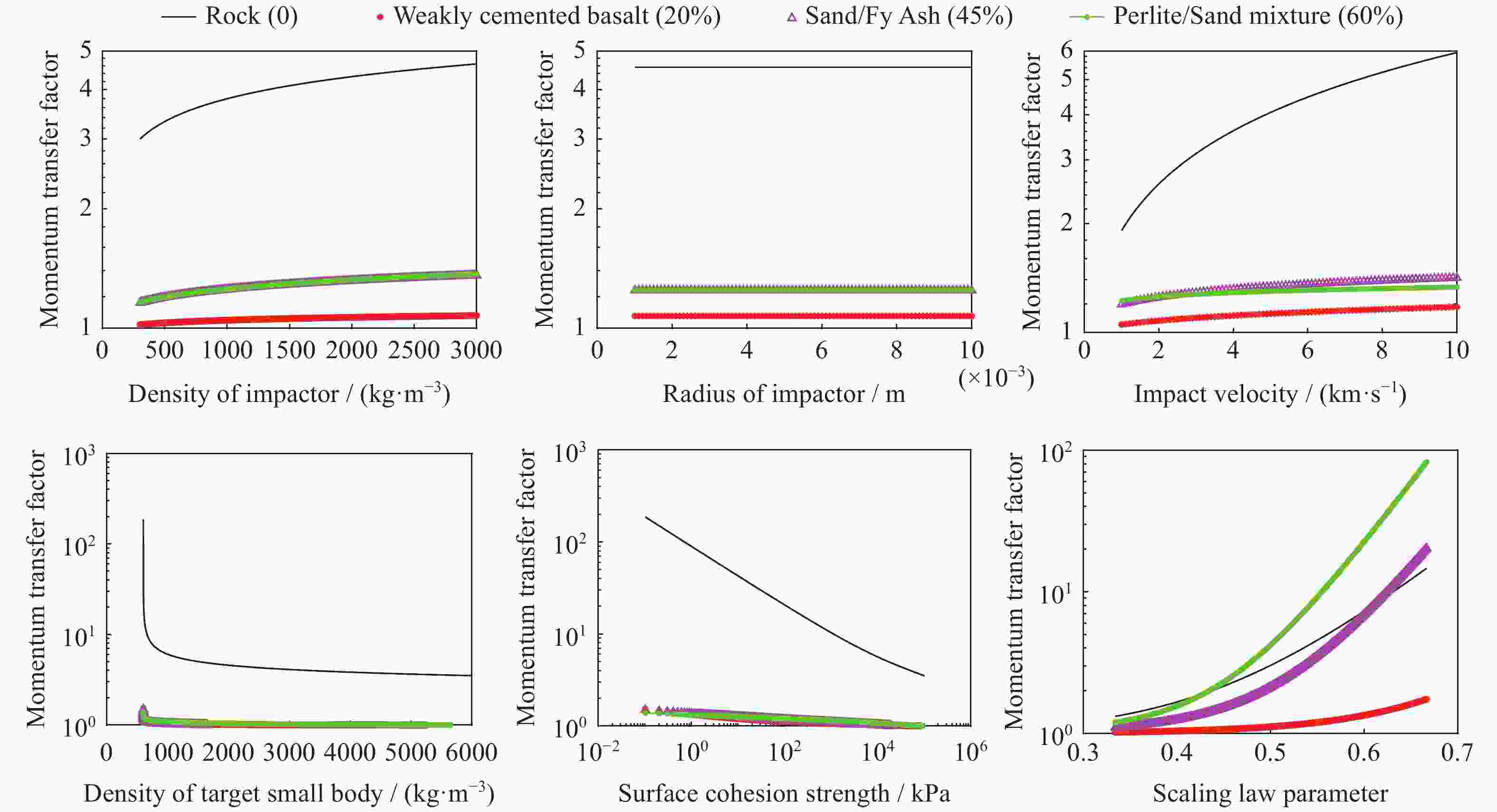
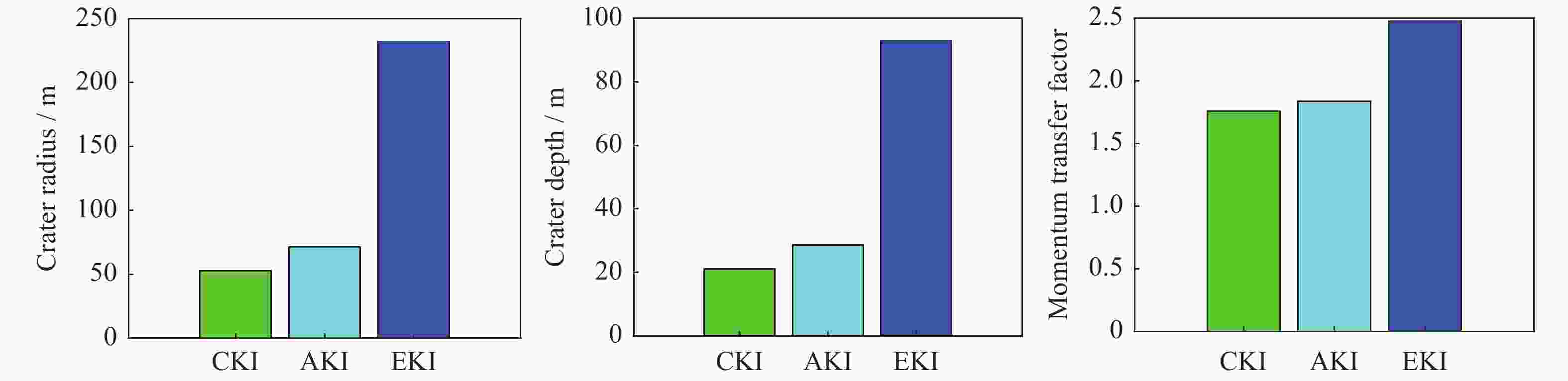
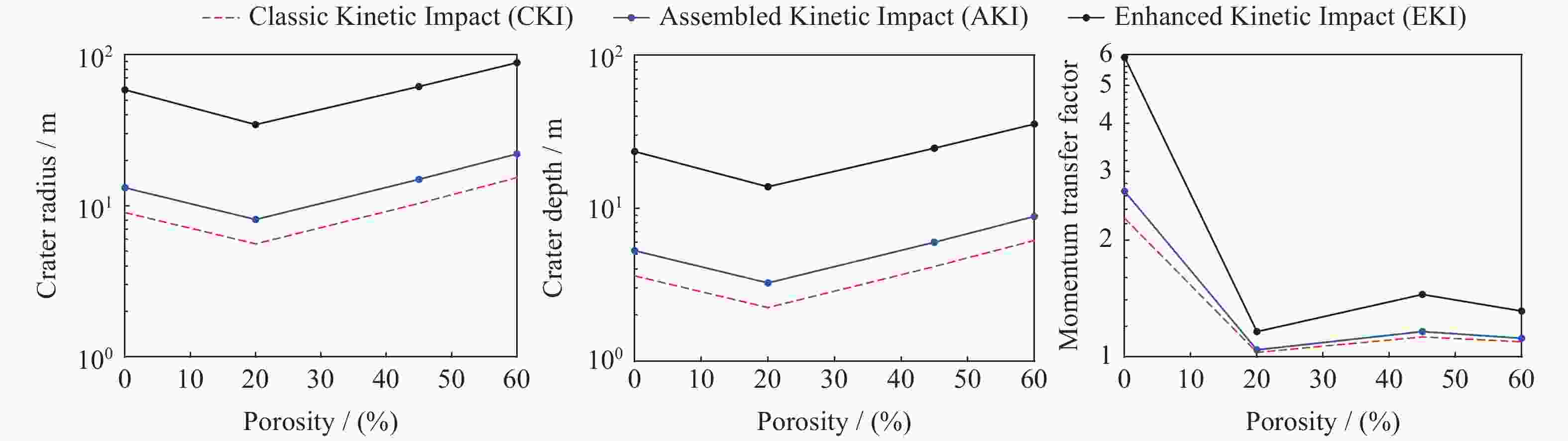
$ \beta $ 是评估动能撞击效果的重要参量。根据动能撞击过程中动量传递因子的理论模型,分析了撞击器特性参数和小天体结构特性参数对动量传递因子取值的影响,并对不同动能撞击方案以及不同材料特性小天体的成坑效应和动量传递因子进行分析。研究表明:标度律参数$ \mu $ 对$ \beta $ 影响较大,$ \mu $ 是地面实验拟合得到的系数,与材料强度特性相关;当小天体为单体岩石结构时,撞击器速度及密度、小天体密度及表面强度对$ \beta $ 影响较大,而撞击器半径和小天体引力对$ \beta $ 影响较小;当小天体为碎石堆结构时,$ \beta $ 对撞击器特性参数和小天体特性参数不敏感,且数值较小。对三种不同动能撞击方案的成坑效应与动量传递因子形成规律进行研究,发现撞击器初始动能对$ \beta $ 影响较大。当小天体为单体岩石结构时,其对应的动量传递因子取值较大,而当小天体为碎石堆结构时,其对应的$ \beta $ 取值较小且基本不变。对相同动能撞击方案下不同材料特性小天体(C型、S型和X型小行星)产生的撞击效应进行分析,发现在引力主导时,βC>βS >βX,而在强度主导时$ \beta $ 取值较小且基本相同。Abstract: Momentum transfer factor β is the key factor to evaluate effect of kinetic impact. In this paper, theoretical model of momentum transfer factor in kinetic impact is investigated, as well as the influence of impactor properties and small body structure properties on the factor. Meanwhile, the crater effect and momentum transfer factor of small bodies with different kinetic impact schemes and structural characteristics are studied. Results show that scaling law parameter μ, a coefficient related to strength properties of target material which is obtained by ground experiment fitting, has a great effect on the factor. The velocity/density of impactor and density/surface strength of small body have a great effect on the factor for small body with a single rock structure, while radius of impactor and gravity of small body have a small effect. In the meantime, the value of β is significant. The factor is insensitive to parameters of impactor properties and small body structure properties for small body with a rubble-pile structure, and its value is close to 1. The formation of crater and momentum transfer factor in three different kinetic impact schemes indicates that the initial kinetic energy of impactor has a great influence on the factor. In the same kinetic impact scheme where gravity dominates the crater formation, the momentum transfer factor of a C-complex asteroid is largest followed by S-complex and X-complex. However, when strength dominates crater formation, the factors of all complexes are smaller and basically the same.-
Key words:
- Kinetic impact /
- Small body defense /
- Momentum transfer factor /
- Scaling law /
- Sensitivity analysis
-
表 1 可参考的材料经验参数
Table 1. Experience parameters of materials
材料结构编号 1 2 3 4 5 主导因素 引 力 强 度 强 度 强 度 强 度 材料类型 粗 砂 石 块 弱胶合玄武岩 致密沙土 珍珠岩/沙土混合物 宏观孔隙率n/(%) $ 35\pm 5 $ 0 20 45 60 $ {\mu } $ 0.41 0.55 0.46 0.4 0.35 $ {\nu } $ 0.4 0.4 0.4 0.4 0.4 $ {{C}}_{1} $ 0.55 1.5 0.18 0.55 0.6 $ {k} $ 0.3 0.3 0.3 0.3 0.32 $ {{H}}_{1} $(引力) 0.59 - - - - $ {{H}}_{2} $(强度) - 1.1 0.38 0.4 0.81 $ {{n}}_{1} $ 1.2 1.2 1.2 1.2 1.2 $ {{n}}_{2,{G}} $(引力) 1.3 - - - - $ {{n}}_{2,{S}} $(强度) - 1 1 1 1 撞击器密度$ {\delta } $/
($ \text{kg}\cdot {\text{m}}^{-3} $)1220 2700 2700 930 940 撞击器半径$ {r}(\times {10}^{-3}) $/
$ \rm{m} $$ 3.9 $ $ 1.6 $ $ 3.6 $ $ 7 $ $ 8.7 $ 撞击速度$ {u} $/
($ \text{km}\cdot {\rm{s}}^{-1} $)6-7 6.2 1.8 1.9 1.8 目标密度$ {\rho } $/
($ \text{kg}\cdot {\text{m}}^{-3} $)1510 3000 2600 1500 1200 引力加速度g/
($ \text{m}\cdot {\text{s}}^{-2} $)9.81 - - - - Y/kPa - $ 3\times {10}^{4} $ $ 4.5\times {10}^{2} $ $ 4 $ $ 2 $ 表 2 特性参数可取值范围
Table 2. Range of property parameters
特性参数 取值范围 备注 撞击速度$ u/ $($ \mathrm{k}\mathrm{m}\cdot {\mathrm{s}}^{-1} $) $ 1 \sim 10 $ 撞击器的典型撞击速度[28,29] 撞击器密度$ \delta / $($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) $ 300 \sim 3000 $ 考虑撞击器类型为两种:人造撞击器或者太空岩石[28,29] 撞击器半径$ \;\;r $($ \times {10}^{-3})/\mathrm{m} $ $ 1 \sim 10 $ 地面针对动能撞击小天体的撞击实验中撞击器半径设定在$ {10}^{-3} \sim {10}^{-2}\;\mathrm{m} $ 量级[4] 小天体密度$ \rho / $($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) $ 600 \sim 6000 $ 考虑小天体中彗星密度最小,金属小行星密度最大[30-32] 小天体引力加速度$ g $($ \times {10}^{-5})/(\mathrm{m}\cdot {\mathrm{s}}^{-2} $) $ 1 \sim 10 $ 考虑小天体典型弱引力场数值在$ {10}^{-5} \sim {10}^{-4}\;\mathrm{m}\cdot {\mathrm{s}}^{-2} $量级[33],小天体尺寸 在6~600 m量级 小天体表面内聚强度$ Y/ $kPa $ 1\times {10}^{-1} \sim 1\times {10}^{5} $ 考虑小天体中彗星的孔隙率较大,表面内聚强度最小,在$ 100\;\mathrm{P}\mathrm{a} $以上,
而金属小行星密度大,表面内聚强度最大,在$ 100\;\mathrm{M}\mathrm{P}\mathrm{a} $左右[30,32]标度律参数$\;\; \mu $ $ 1/3 < \mu < 2/3 $ $ \mu $取值范围为其最大可取范围[4,20] 表 3 引力/强度主导时参数与动量传递因子相关性
Table 3. Correlation between parameters and momentum transfer factor when gravity/strength dominates
参数 主导因素 与 $ \beta $ 的相关性 参数$ \mu $ 引力/强度主导 正相关 撞击器密度$ \delta / $($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) 引力/强度主导 正相关 撞击器半径$ r $($ \times {10}^{-3})/\mathrm{m} $ 引力主导 负相关 强度主导 不相关 撞击速度$ u/ $($ \mathrm{k}\mathrm{m}\cdot {\mathrm{s}}^{-1} $) 引力/强度主导 正相关 小天体密度$ \rho / $($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) 引力/强度主导 负相关 小天体引力加速度$ g $ ($ \times {10}^{-5})/(\mathrm{m}\cdot {\mathrm{s}}^{-2} $) 引力/强度主导 负相关 小天体表面内聚强度$ Y/ $kPa 引力/强度主导 负相关 表 4 Apophis小行星参数
Table 4. Parameters of Apophis asteroid
参数 遥感探测数据 小行星直径$ R/\mathrm{m} $ $ {375}_{-10}^{+14} $ 小行星密度$ \rho / $($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) $ (3.2\pm 0.2)\times {10}^{3} $(LL型球粒陨石) 小行星宏观孔隙率$ n/ $(%) $ 0 \sim 50 $(平均:20) 小行星质量$ M $($ \times {10}^{10})/\mathrm{k}\mathrm{g} $ $ 4.4 \sim 6.2 $
(平均:$ 5.3\pm 0.9 $)小行星引力加速度$ g $($ \times {10}^{-5})/(\mathrm{m}\cdot {\mathrm{s}}^{-2} $) $ 8.3511 \sim 11.767 $ 小行星表面逃逸速度$ {v}_{\mathrm{e}\mathrm{s}\mathrm{c}}/ $($ \mathrm{m}\cdot {\mathrm{s}}^{-1} $) $ 0.1770 \sim 0.2101 $ 表 5 三种不同动能撞击器参数
Table 5. Parameters for kinetic impactors of three types
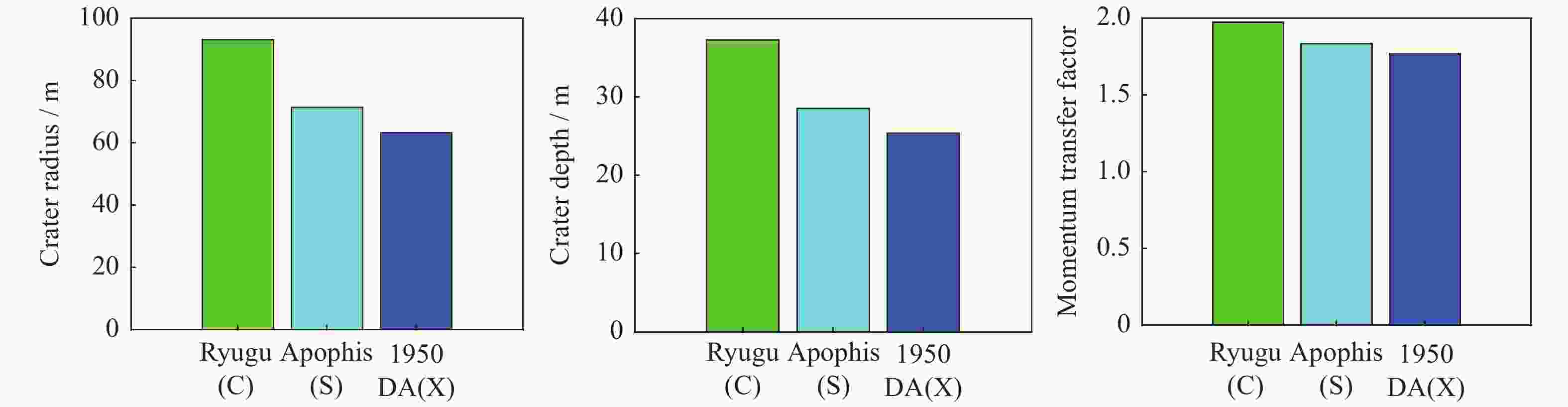
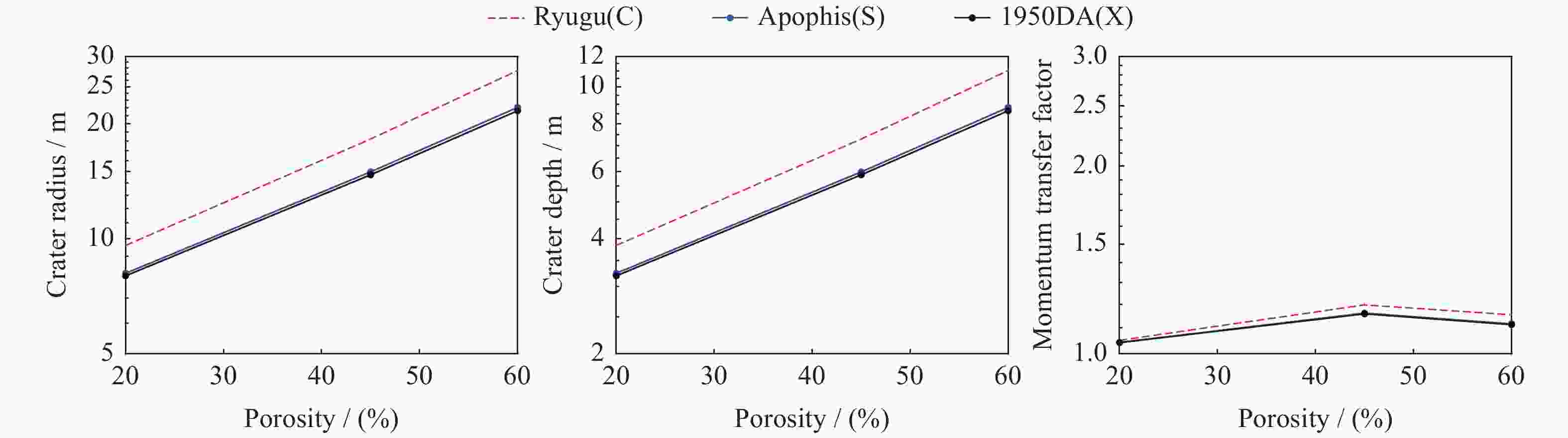
参数 经典动能撞击 含末级动能撞击 以石击石加强型动能撞击 纯铝材料 纯铝材料 岩石材料 有效密度$ \delta / $($ \mathrm{k}\text{g}\cdot {\text{m}}^{-3} $) $ 74.6129 $ $ 118.8501 $ $ 1457.1070 $ 质量$ m(\times {10}^{3})/\mathrm{k}\mathrm{g} $ $ 3.56 $ $ 8.75 $ $ 200 $ 半径$ r/\mathrm{m} $ $ 2.25 $ $ 2.6 $ $ 3.2 $ 撞击速度$ u/ $($ \mathrm{k}\mathrm{m}\cdot {\mathrm{s}}^{-1} $) $ 6.57 $ $ 7.17 $ $ 12 $ 撞击动能$ {E}_{{\rm{imp}}}(\times {10}^{10})/\mathrm{J} $ $ 7.6834 $ $ 22.491 $ $ 1440 $ 撞击角$ \varphi / $(°) $ 90 $ $ 90 $ $ 90 $ 表 6 不同类型小行星参数
Table 6. Parameters for asteroids of different types
参数 Ryugu小行星 Apophis小行星 1950 DA小行星 小行星直径$ R/\mathrm{m} $ $ \left(1.04\times 1.02\times 0.88\right)\times {10}^{3} $ $ {375}_{-10}^{+14} $ $ \left(1.25\pm 0.12\right)\times {10}^{3} $ 小行星密度$ \rho (\times {10}^{3}) $/($ \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3} $) $ 1.19\pm 0.02 $ $ 3.2\pm 0.2 $ $ 3.5\pm 0.35 $ 小行星宏观孔隙率n/(%) $ > 50 $(高孔隙率) $ 0 \sim 50 $(平均 :20) $ 51\pm 19 $ 小行星质量$ M(\times {10}^{10})/\mathrm{k}\mathrm{g} $ $ 44.975 $ $ 4.4 \sim 6.2 $
(平均:$ 5.3\pm 0.9 $)$ 399 $ 小行星引力加速度$ g $
($ \times {10}^{-5})/(\mathrm{m}\cdot {\mathrm{s}}^{-2} $)$ 12 $ $ 8.3511 \sim 11.767 $ $ 14.185 \sim 20.850 $ 小行星表面逃逸速度$ {v}_{\mathrm{e}\mathrm{s}\mathrm{c}}/ $($ \mathrm{m}\cdot {\mathrm{s}}^{-1} $) $ 0.3652 $ $ 0.1770 \sim 0.2101 $ $ 0.6234 \sim 0.6865 $ -
[1] HOLSAPPLE K A, HOUSEN K R. Momentum transfer in asteroid impacts. I. Theory and scaling[J]. Icarus, 2012, 221(2): 875-887 doi: 10.1016/j.icarus.2012.09.022 [2] SYAL M B, OWEN J M, MILLER P L. Deflection by kinetic impact: sensitivity to asteroid properties[J]. Icarus, 2016, 269: 50-61 doi: 10.1016/j.icarus.2016.01.010 [3] GAULT D E, SHOEMAKER E M, MOORE H J, et al. Spray Ejected from the Lunar Surface by Meteoroid Impact[R]. Washington: National Aeronautics and Space Administration, 1963 [4] HOUSEN K R, HOLSAPPLE K A. Ejecta from impact craters[J]. Icarus, 2011, 211(1): 856-875 doi: 10.1016/j.icarus.2010.09.017 [5] MICHEL P. Physical properties of Near-Earth Objects that inform mitigation[J]. Acta Astronautica, 2013, 90(1): 6-13 doi: 10.1016/j.actaastro.2012.07.022 [6] DELCHAMBRE S, ZIEGLER T, FALKE A, et al. Momentum enhancement factor estimation for asteroid redirect missions[J]. Acta Astronautica, 2018, 151: 125-136 doi: 10.1016/j.actaastro.2018.05.050 [7] DEARBORN D S P, SYAL M B, BARBEE B W, et al. Options and uncertainties in planetary defense: impulse-dependent response and the physical properties of asteroids[J]. Acta Astronautica, 2020, 166: 290-305 doi: 10.1016/j.actaastro.2019.10.026 [8] WALKER J D, CHOCRON S, DURDA D D, et al. Momentum enhancement from aluminum striking granite and the scale size effect[J]. International Journal of Impact Engineering, 2013, 56: 12-18 doi: 10.1016/j.ijimpeng.2012.08.003 [9] HOERTH T, SCHÄFER F, HUPFER J, et al. Momentum transfer in hypervelocity impact experiments on rock targets[J]. Procedia Engineering, 2015, 103: 197-204 doi: 10.1016/j.proeng.2015.04.027 [10] FLYNN G J, DURDA D D, PATMORE E B, et al. Momentum enhancement from hypervelocity crater ejecta: implications for the AIDA target[C]//(Abstract) European Planetary Science Congress 2017. Riga: EPSC, 2017, 11: EPSC2017-292 [11] CHENG A F, MICHEL P, JUTZI M, et al. Asteroid impact & deflection assessment mission: kinetic impactor[J]. Planetary and Space Science, 2016, 121: 27-35 doi: 10.1016/j.pss.2015.12.004 [12] MICHEL P, CHENG A, KÜPPERS M, et al. Science case for the asteroid impact mission (AIM): a component of the asteroid impact & deflection assessment (AIDA) mission[J]. Advances in Space Research, 2016, 57(12): 2529-2547 doi: 10.1016/j.asr.2016.03.031 [13] STICKLE A M, RAINEY E S G, SYAL M B, et al. Modeling impact outcomes for the Double Asteroid Redirection Test (DART) mission[J]. Procedia Engineering, 2017, 204: 116-123 doi: 10.1016/j.proeng.2017.09.763 [14] LUTHER R, ZHU M H, COLLINS G, et al. Effect of target properties and impact velocity on ejection dynamics and ejecta deposition[J]. Meteoritics & Planetary Science, 2018, 53(8): 1705-1732 [15] RADUCAN S D, DAVISON T M, LUTHER R, et al. The role of asteroid strength, porosity and internal friction in impact momentum transfer[J]. Icarus, 2019, 329: 282-295 doi: 10.1016/j.icarus.2019.03.040 [16] QUAIDE W L, OBERBECK V R. Thickness determinations of the lunar surface layer from lunar impact craters[J]. Journal of Geophysical Research, 1968, 73(16): 5247-5270 doi: 10.1029/JB073i016p05247 [17] RADUCAN S D, DAVISON T M, COLLINS G S. The effects of asteroid layering on ejecta mass-velocity distribution and implications for impact momentum transfer[J]. Planetary and Space Science, 2020, 180: 104756 doi: 10.1016/j.pss.2019.104756 [18] WARNER B D, HARRIS A W, PRAVEC P. The asteroid lightcurve database[J]. Icarus, 2009, 202(1): 134-146 doi: 10.1016/j.icarus.2009.02.003 [19] SÁNCHEZ P, SCHEERES D J. Rotational evolution of self-gravitating aggregates with cores of variable strength[J]. Planetary and Space Science, 2018, 157: 39-47 doi: 10.1016/j.pss.2018.04.001 [20] HOLSAPPLE K A, SCHMIDT R M. Point source solutions and coupling parameters in cratering mechanics[J]. Journal of Geophysical Research: Atmospheres, 1987, 92(B7): 6350-6376 doi: 10.1029/JB092iB07p06350 [21] ARAKAWA M, WADA K, SAIKI T, et al. Scientific objectives of small carry-on impactor (SCI) and Deployable Camera 3 digital (DCAM3-D): observation of an ejecta curtain and a crater formed on the surface of Ryugu by an artificial high-velocity impact[J]. Space Science Reviews, 2017, 208(1/2/3/4): 187-212 [22] RICHARDSON J E, MELOSH H J, LISSE C M, et al. A ballistics analysis of the deep impact ejecta plume: determining comet tempel 1's gravity, mass, and density[J]. Icarus, 2007, 190(2): 357-390 doi: 10.1016/j.icarus.2007.08.001 [23] HOLSAPPLE K A, HOUSEN K R. A crater and its ejecta: an interpretation of Deep Impact[J]. Icarus, 2007, 191(2): 586-597 doi: 10.1016/j.icarus.2006.08.035 [24] ERNST C M, SCHULTZ P H. Evolution of the Deep Impact flash: implications for the nucleus surface based on laboratory experiments[J]. Icarus, 2007, 190(2): 334-344 doi: 10.1016/j.icarus.2007.03.030 [25] HERMALYN B, SCHULTZ P H, COLAPRETE A. LCROSS ejecta dynamics: insight from experiments[C]//41 st Lunar and Planetary Science Conference. Texas: Lunar and Planetary Institute, 2010 [26] CHENG A F, STICKLE A M, FAHNESTOCK E G, et al. DART mission determination of momentum transfer: model of ejecta plume observations[J]. Icarus, 2020, 352: 113989 doi: 10.1016/j.icarus.2020.113989 [27] CHENG A F, RIVKIN A S, MICHEL P, et al. AIDA DART asteroid deflection test: planetary defense and science objectives[J]. Planetary and Space Science, 2018, 157: 104-115 doi: 10.1016/j.pss.2018.02.015 [28] WANG Y R, LI M T, GONG Z Z, et al. Assembled Kinetic Impactor for Deflecting Asteroids by Combining the Spacecraft with the Launch Vehicle Upper Stage[J]. Icarus, 2021, 368: 114596 doi: 10.1016/j.icarus.2021.114596 [29] LI M T, WANG Y R, WANG Y L, et al. Enhanced kinetic impactor for deflecting large potentially hazardous asteroids via maneuvering space rocks[J]. Scientific Reports, 2020, 10(1): 8506 doi: 10.1038/s41598-020-65343-z [30] BRITT D T, YEOMANS D, HOUSEN K, et al. Asteroid density, porosity, and structure[M]//BOTTKE W F, CELLINO A, PAOLICCHI P, et al. Asteroids III. Tucson: University of Arizona Press, 2002: 485-500 [31] CARRY B. Density of asteroids[J]. Planetary and Space Science, 2012, 73(1): 98-118 doi: 10.1016/j.pss.2012.03.009 [32] BIELE J, ULAMEC S, RICHTER L, et al. The putative mechanical strength of comet surface material applied to landing on a comet[J]. Acta Astronautica, 2009, 65(7/8): 1168-1178 [33] BRISSET J, COLWELL J, DOVE A, et al. Regolith behavior under asteroid-level gravity conditions: low-velocity impact experiments[J]. Progress in Earth and Planetary Science, 2018, 5(1): 73 doi: 10.1186/s40645-018-0222-5 [34] BINZEL R P, RIVKIN A S, THOMAS C A, et al. Spectral properties and composition of potentially hazardous Asteroid (99942) Apophis[J]. Icarus, 2009, 200(2): 480-485 doi: 10.1016/j.icarus.2008.11.028 [35] MÜLLER T G, KISS C, SCHEIRICH P, et al. Thermal infrared observations of asteroid (99942) Apophis with Herschel[J]. Astronomy & Astrophysics, 2014, 566: A22 [36] TAKIZAWA S, KATSURAGI H. Scaling laws for the oblique impact cratering on an inclined granular surface[J]. Icarus, 2020, 335: 113409 doi: 10.1016/j.icarus.2019.113409 [37] KOVÁČOVÁ M, NAGY R, KORNOŠ L, et al. 101955 Bennu and 162173 Ryugu: dynamical modelling of ejected particles to the Earth[J]. Planetary and Space Science, 2020, 185: 104897 doi: 10.1016/j.pss.2020.104897 [38] OKADA T, FUKUHARA T, TANAKA S, et al. Highly porous nature of a primitive asteroid revealed by thermal imaging[J]. Nature, 2020, 579(7800): 518-522 doi: 10.1038/s41586-020-2102-6 [39] WATANABE S, HIRABAYASHI M, HIRATA N, et al. Hayabusa2 arrives at the carbonaceous asteroid 162173 Ryugu-A spinning top-shaped rubble pile[J]. Science, 2019, 364(6437): 268-272 doi: 10.1126/science.aav8032 [40] GUNDLACH B, BLUM J. Regolith grain size and cohesive strength of near-Earth Asteroid (29075) 1950 DA[J]. Icarus, 2015, 257: 126-129 doi: 10.1016/j.icarus.2015.04.032 [41] FARNOCCHIA D, CHESLEY S R. Assessment of the 2880 impact threat from Asteroid (29075) 1950 DA[J]. Icarus, 2014, 229: 321-327 doi: 10.1016/j.icarus.2013.09.022 [42] BUSCH M W, GIORGINI J D, OSTRO S J, et al. Physical modeling of near-Earth Asteroid (29075) 1950 DA[J]. Icarus, 2007, 190(2): 608-621 doi: 10.1016/j.icarus.2007.03.032 -
-







 下载:
下载: