一种基于递推最小二乘法的运动平台剩磁差分测量与估计方法
doi: 10.11728/cjss2024.03.2023-0002 cstr: 32142.14.cjss2024.03.2023-0002
Remanence Model Estimation Method of Geomagnetic Navigation Carrier Based on Recursive Least Square Method
-
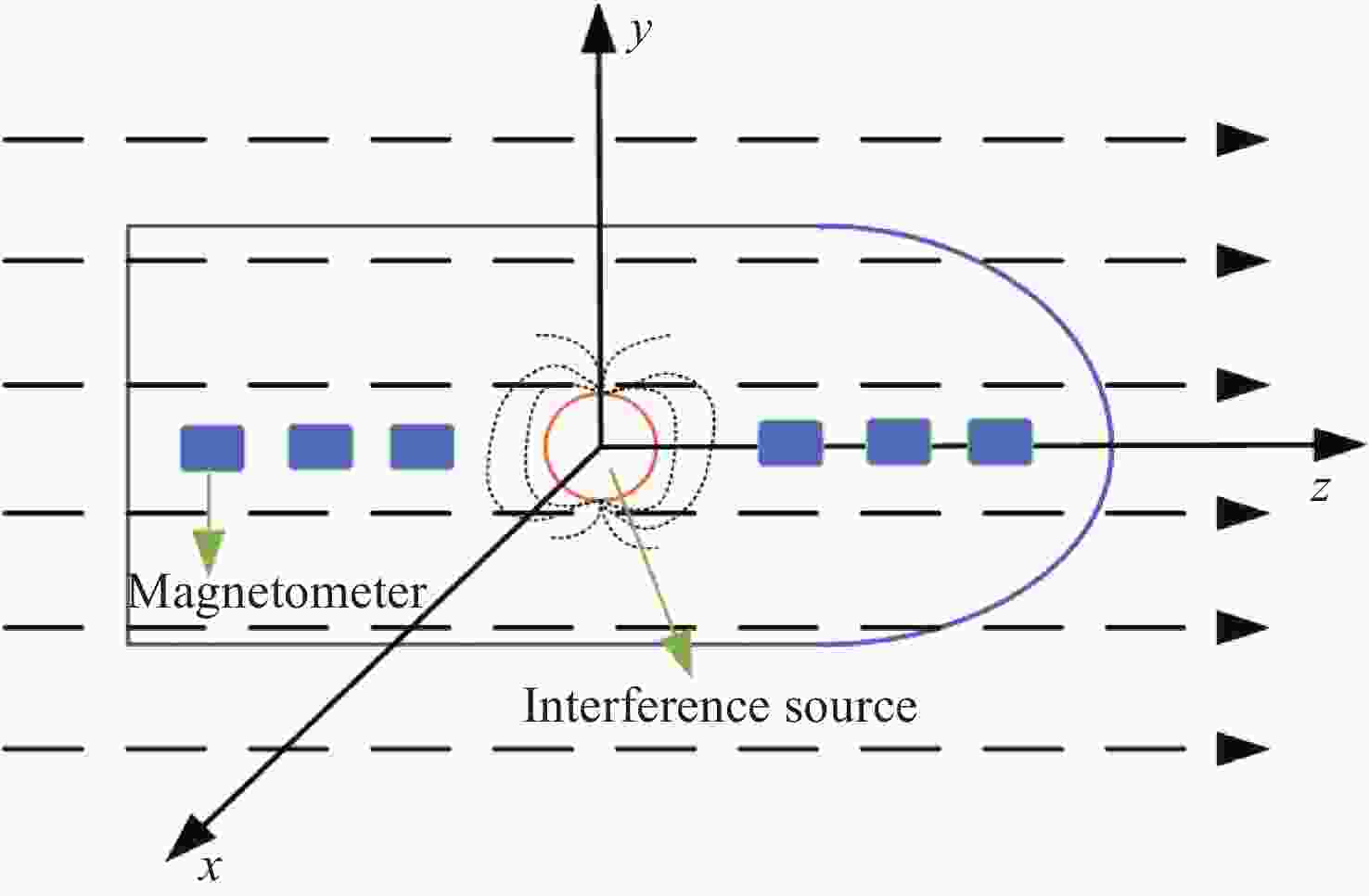
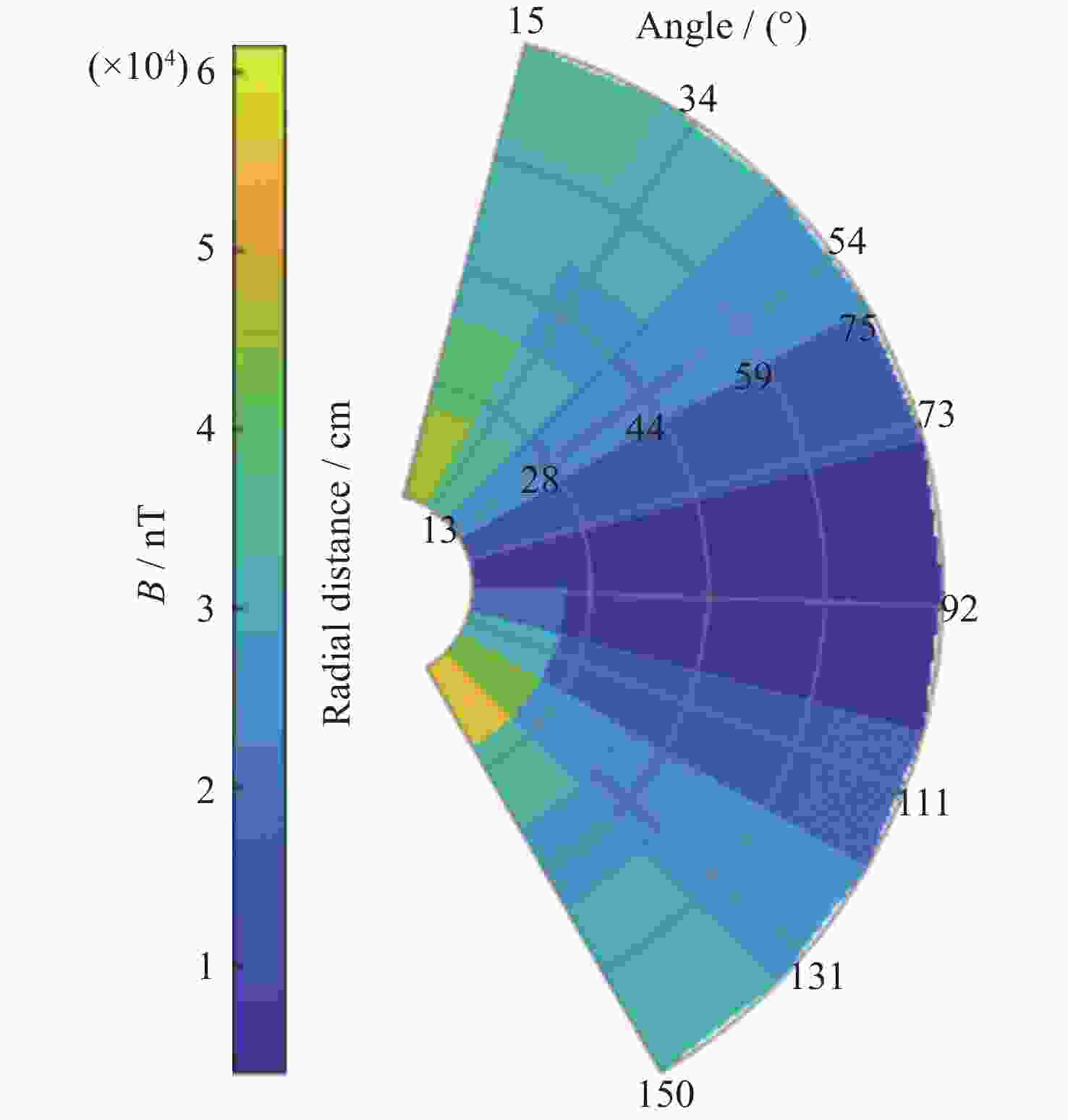
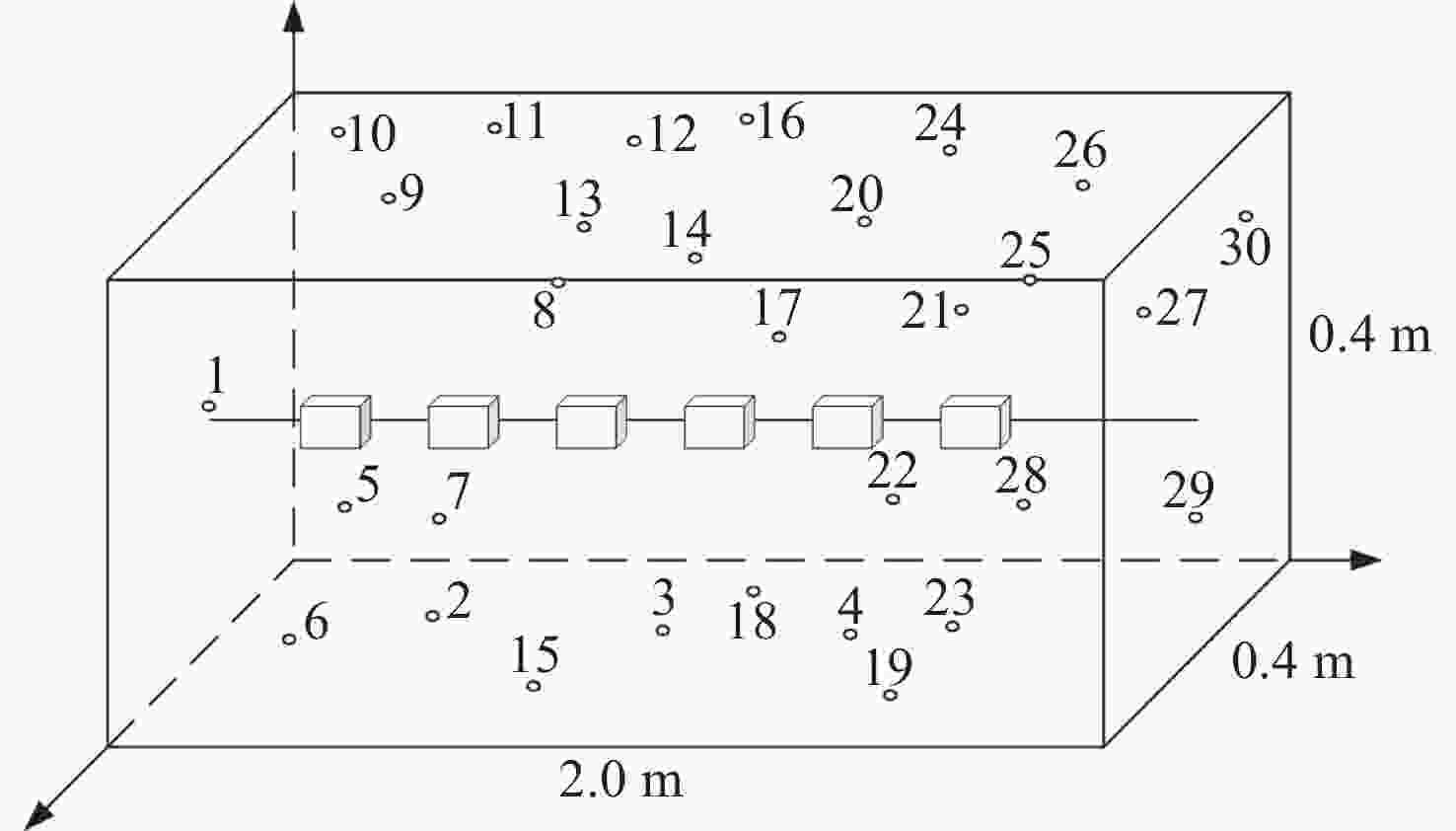
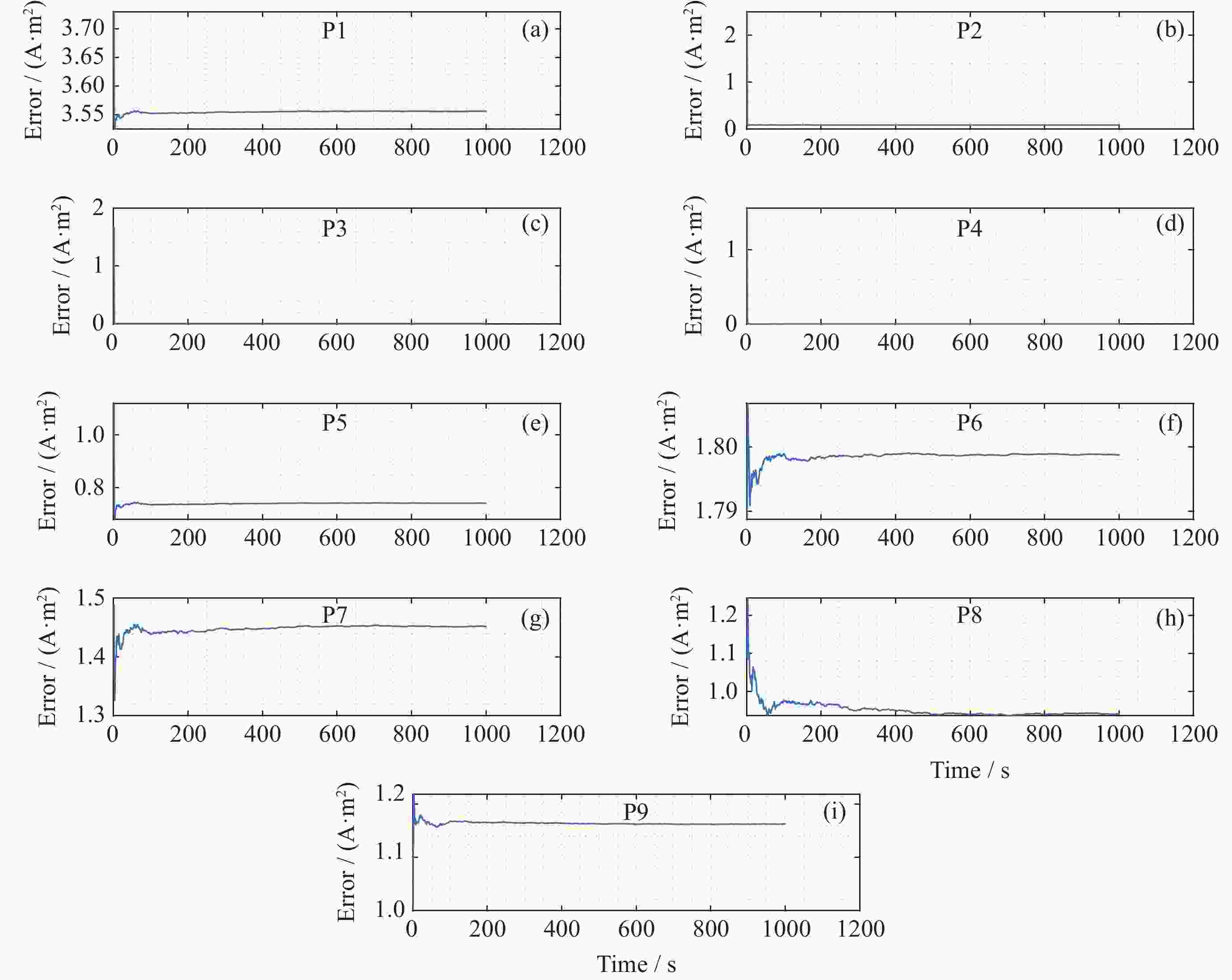
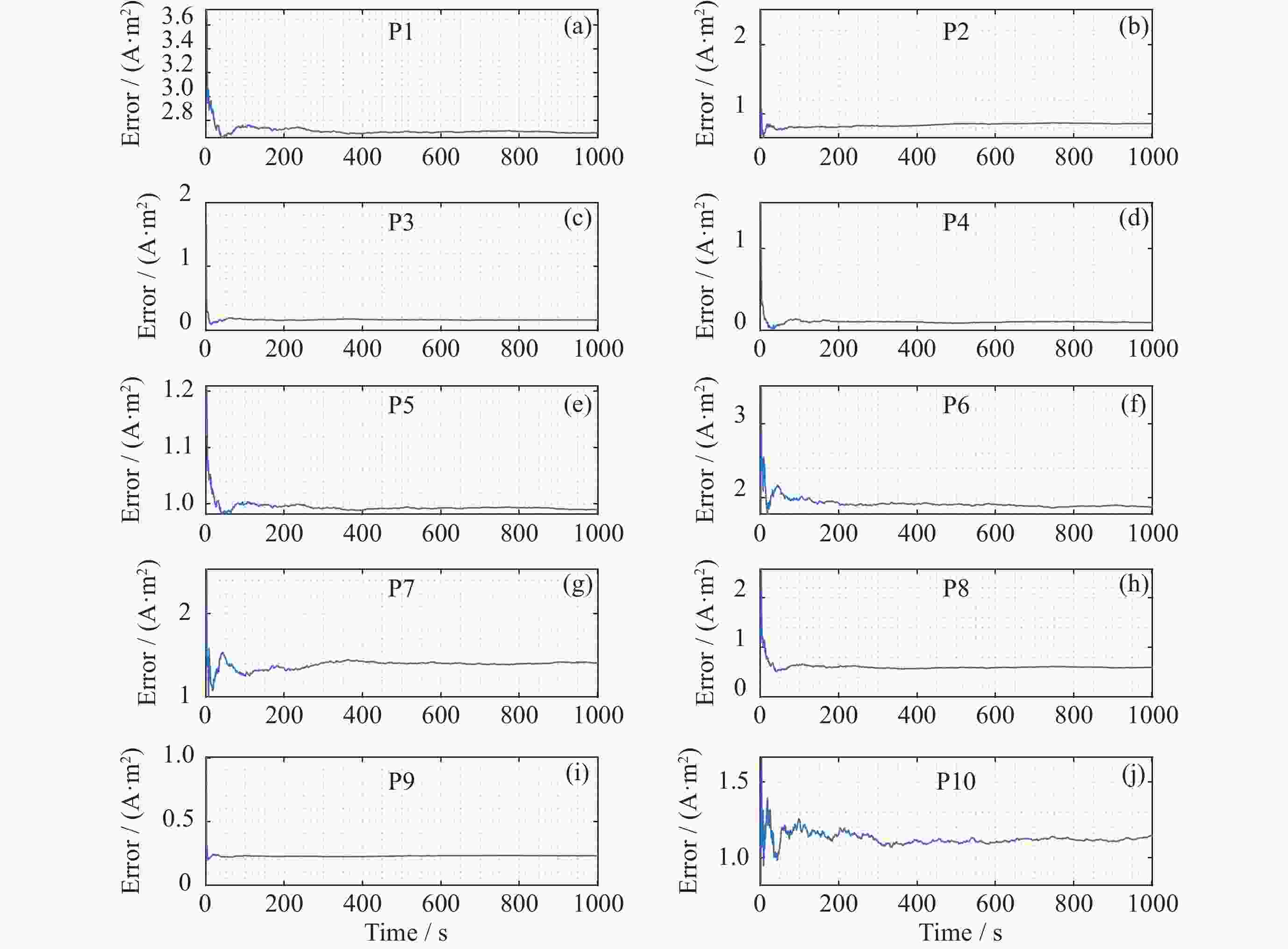
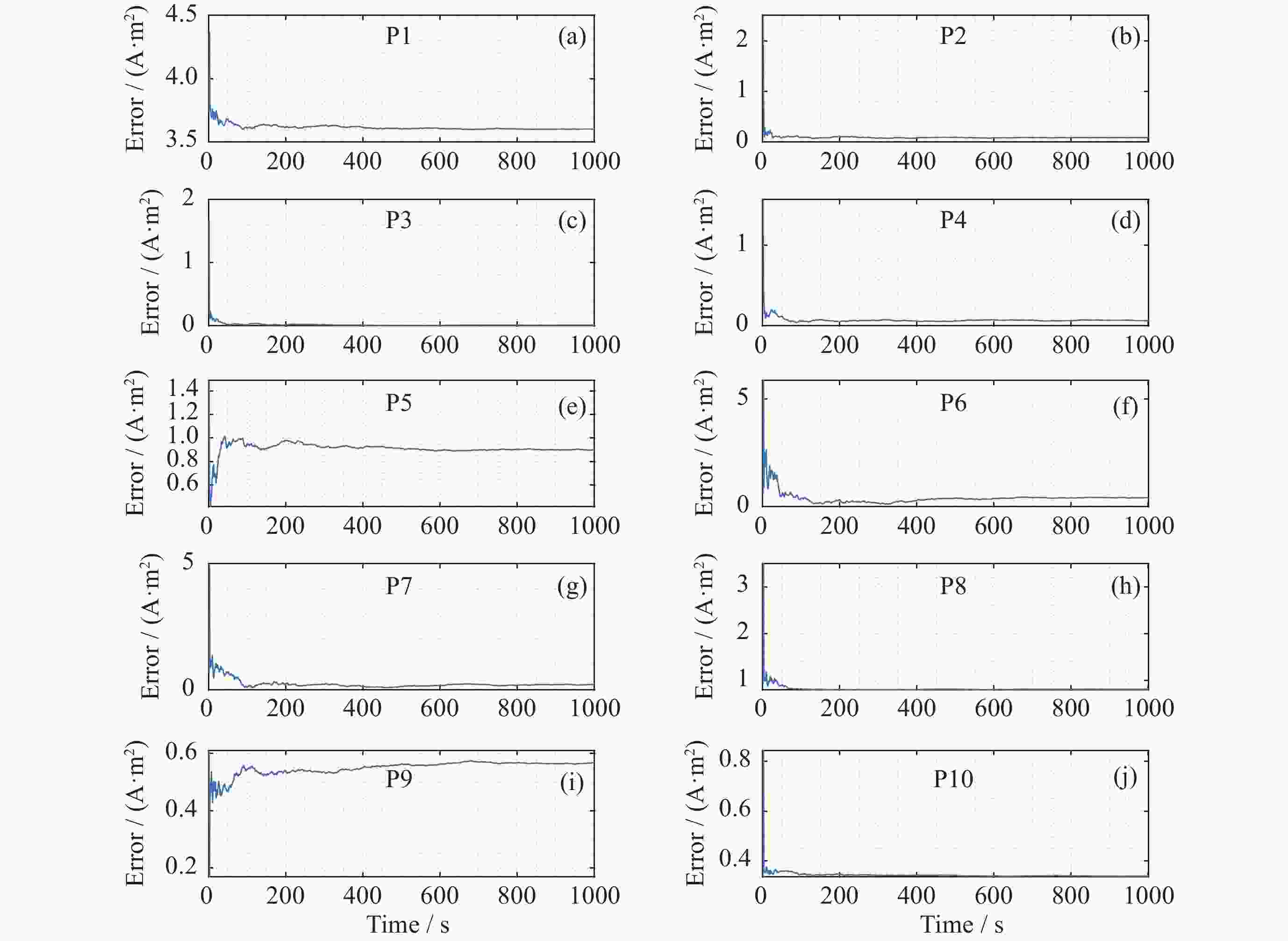
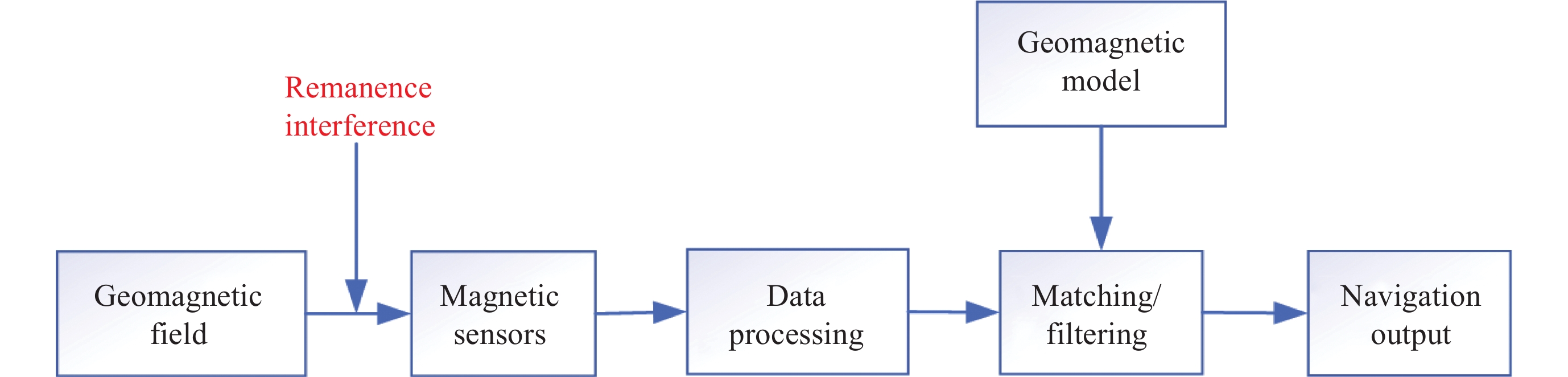
摘要: 地磁导航是通过对地球周围矢量磁场进行测量从而实现导航的一种方法. 地磁导航在运动平台上应用的难点之一是平台剩磁对地磁测量的影响, 严重污染了磁强计的测量. 消除平台剩磁对地磁测量的影响成为地磁导航向应用转化的一项关键技术. 为实现运动平台剩磁的有效测量与估计, 提出了基于递推最小二乘法的运动平台剩磁差分测量与估计方法. 基于载体干扰磁场值只与测量点到磁偶极子的距离和磁偶极子的磁矩有关的结论, 根据磁偶极子的磁场分布特性, 推导出一种基于内置磁强计阵列的运动平台剩磁差分估计模型, 并通过递推最小二乘法求解差分估计模型. 大量仿真实验表明, 可以通过内置阵列磁强计对平台剩磁进行测量与估计, 验证了所提出的平台剩磁估计方法的有效性.Abstract: Geomagnetic navigation is a method of in-situ measurement of magnetic field by the magnetometer installed on the carrier platform to realize navigation. It is a passive navigation, which has the advantages of autonomy, strong anti-interference ability and no cumulative error. One of the difficulties in the application of geomagnetic navigation on moving platform is the influence of platform remanence on geomagnetic measurement, which seriously pollutes the measurement of magnetometer and becomes a key technology in the transformation of geomagnetic navigation to application. For example, the magnetic field distribution generated by ferromagnetic materials and the interference magnetic field generated by electrical equipment during work will pollute the measured value of the magnetometer, and then affect the accuracy of geomagnetic navigation. Aiming at the complicated problem of interfering magnetic field in geomagnetic measurement, this paper focuses on the effective measurement and estimation of the remanence of a moving platform. In order to realize effective measurement and estimation of remanence of moving platform, a method of differential measurement and estimation of remanence of moving platform based on recursive least square method is proposed. Firstly, the method is based on the conclusion that the carrier interference magnetic field value is only related to the distance between the measuring point and the magnetic dipole and the equivalent magnetic moment of the magnetic dipole in magnetic dipole theory, and the magnetic field distribution characteristics of the magnetic dipole. A remanence difference estimation model of moving platform based on built-in magnetometer array is derived, and the difference estimation model is solved by recursive least square method. Finally, a large number of simulation experiments show that the platform remanence estimation method can be measured and estimated by the built-in array magnetometer, which proves the effectiveness of the proposed method and lays a theoretical foundation for accurate geomagnetic navigation.
-
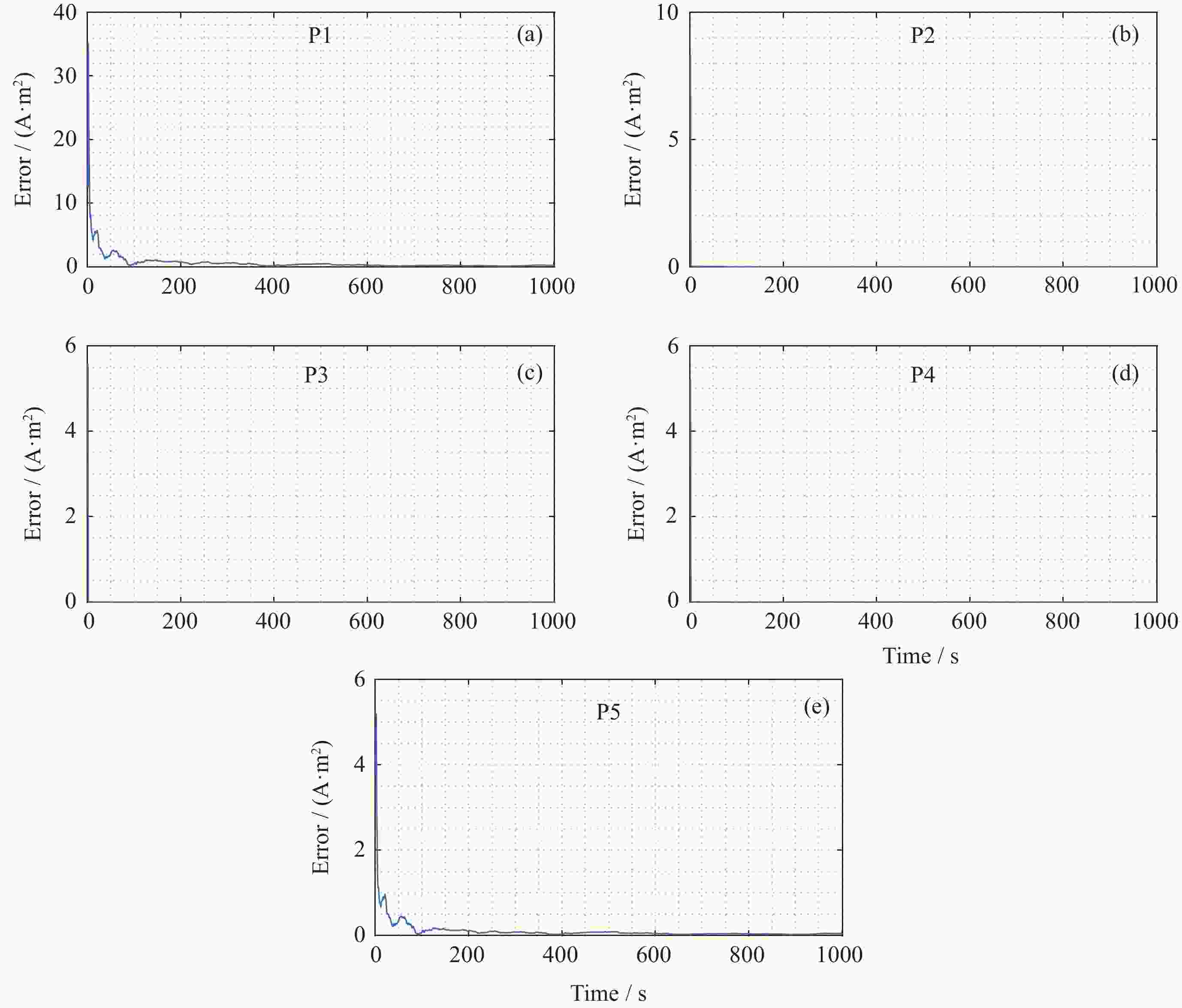
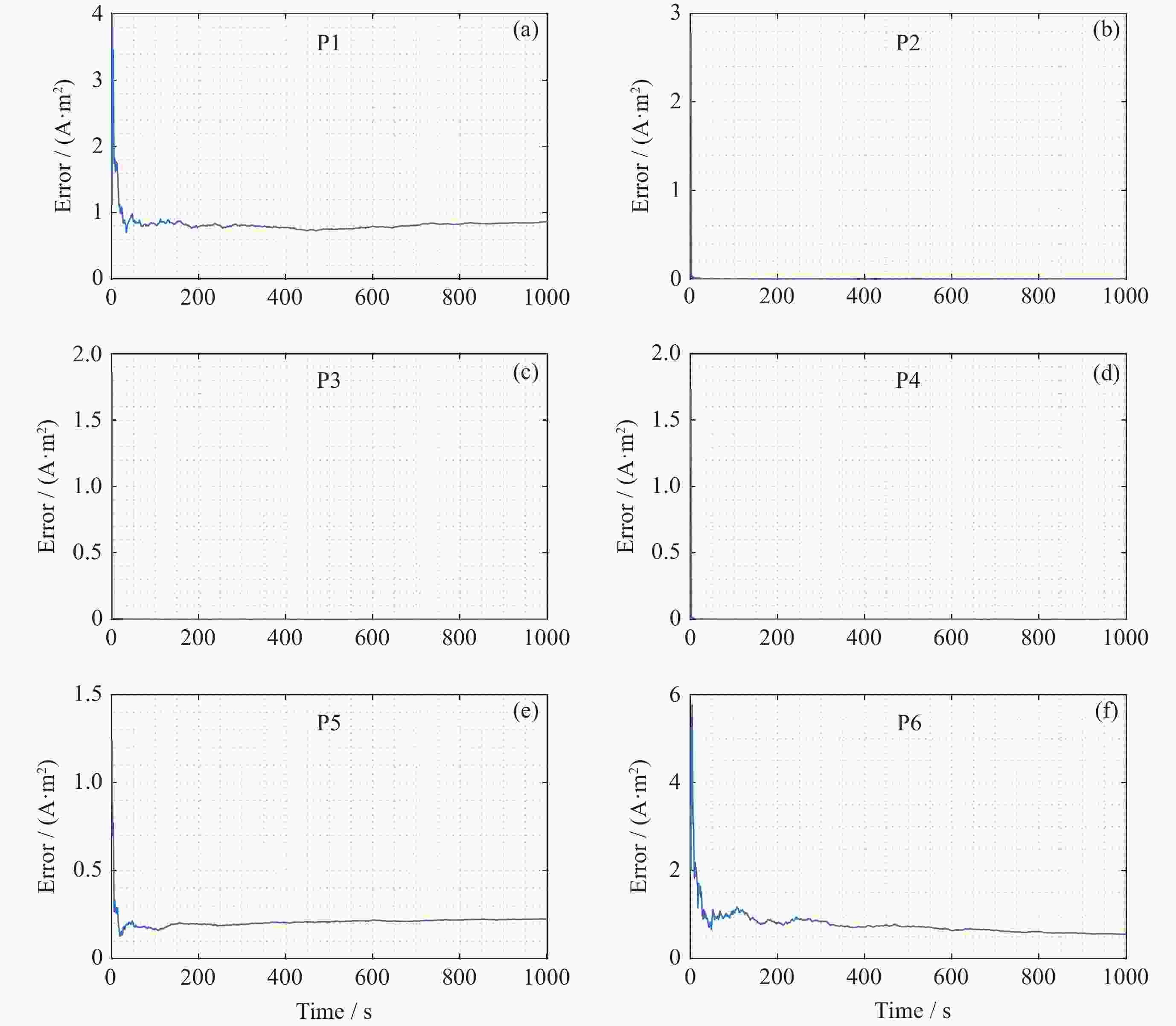
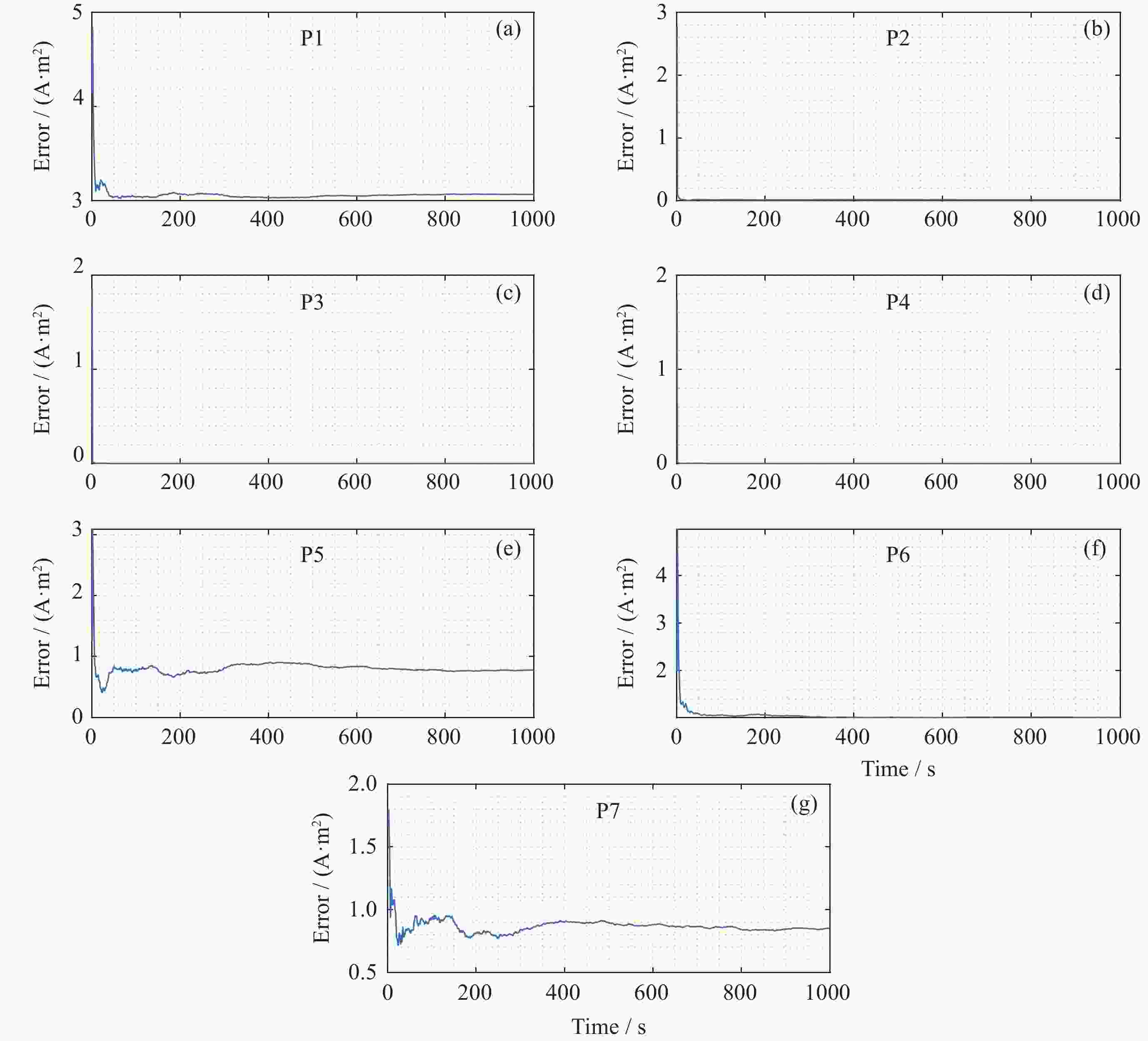
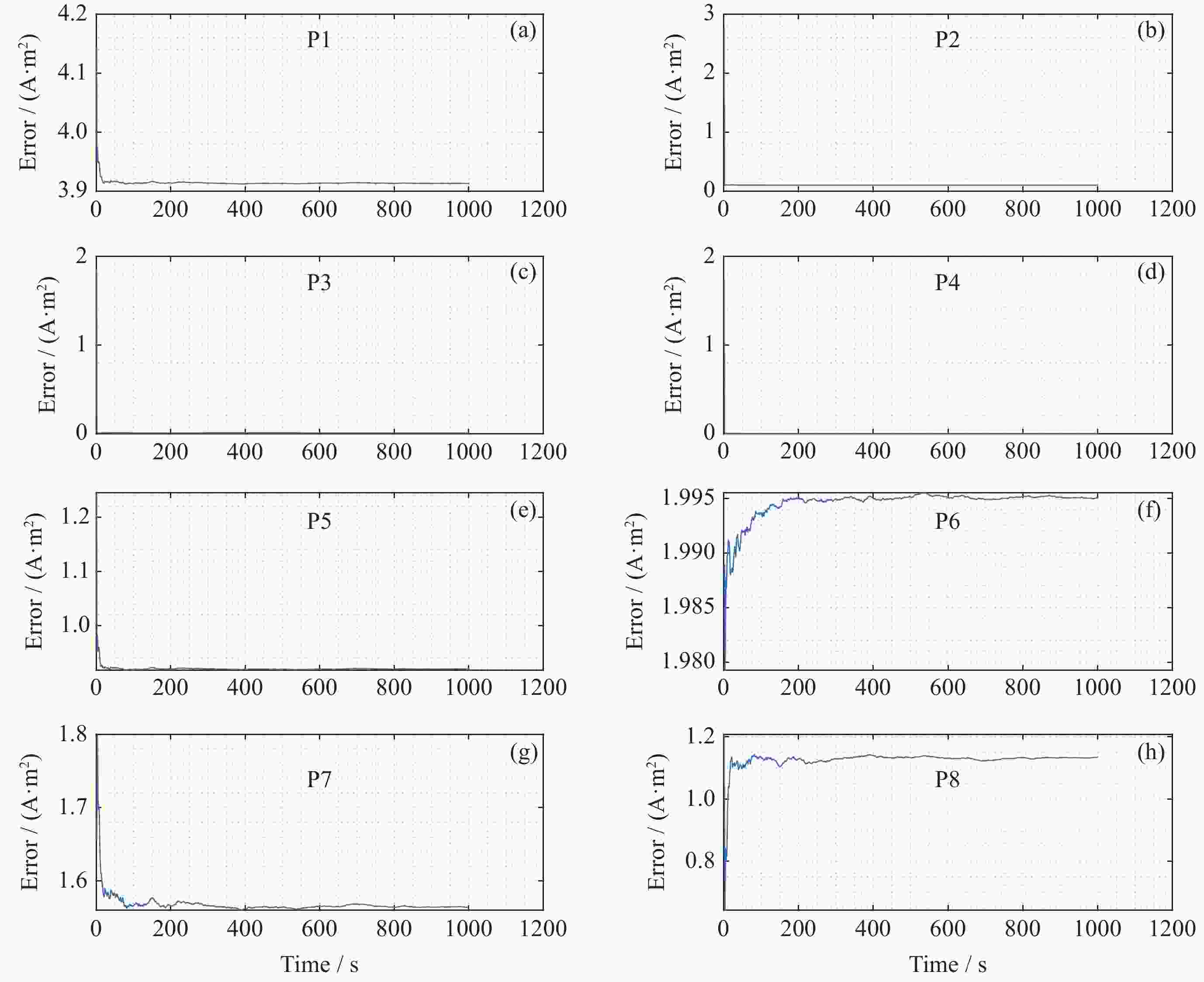
表 1 m=5, n=6时磁偶极子误差百分比
Table 1. Error percentage of magnetic dipole when m=5 and n=6
磁偶极子序号 误差百分比值/(%) 1 0.76183 2 0.00672 3 0.00343 4 0.00404 5 0.00538 表 2 m=6, n=6时磁偶极子误差百分比
Table 2. Error percentage of magnetic dipole when m=6 and n=6
磁偶极子序号 误差百分比值/(%) 1 6.03741 2 0.03409 3 0.00509 4 0.00363 5 4.33320 6 8.05160 表 3 m=7, n=6时磁偶极子误差百分比
Table 3. Error percentage of magnetic dipole when m=7 and n=6
磁偶极子序号 误差百分比值 /(%) 1 7.45261 2 0.05124 3 0.00446 4 0.00398 5 6.20780 6 5.06344 7 4.72406 表 4 m=8, n=6时磁偶极子误差百分比
Table 4. Error percentage of magnetic dipole when m=8 and n=6
磁偶极子序号 误差百分比值/ (%) 1 9.43795 2 0.37934 3 0.05351 4 0.01930 5 7.37411 6 9.03933 7 9.40990 8 9.51667 表 5 m=9, n=6时磁偶极子误差百分比
Table 5. Error percentage of magnetic dipole when m=9 and n=6
磁偶极子序号 误差百分比值/(%) 1 8.57700 2 0.32214 3 0.04867 4 0.01976 5 5.92758 6 9.05313 7 8.74328 8 7.89434 9 9.40489 表 6 m=10, n=6时磁偶极子误差百分比
Table 6. Error percentage of magnetic dipole when m=10 and n=6
磁偶极子序号 误差百分比值/(%) 1 8.60312 2 0.30705 3 0.12553 4 0.12544 5 6.20852 6 9.14841 7 8.75330 8 9.51979 9 9.92289 10 8.76301 表 7 均匀分布下m=10, n=6时磁偶极子的误差百分比
Table 7. Magnetic dipole error percentage when m=10 and n=6 under uniform distribution
磁偶极子序号 误差百分比值/(%) 1 8.77522 2 0.28271 3 0.13561 4 0.39641 7 5.38940 13 5.88672 20 1.73264 22 7.67923 26 8.03289 29 9.18390 -
[1] LIU Y X, ZHANG P, WANG X. Information fusing algorithm in inertial/geomagnetic navigation system[C]//Proceedings of 2020 International Conference on Guidance, Navigation and Control, ICGNC 2020. Tianjin: Springer, 2022: 1219-1227 [2] MA X J, LIU H W, XIAO D, et al. Key technologies of geomagnetic aided inertial navigation system[C]//2009 IEEE Intelligent Vehicles Symposium. Xi'an: IEEE, 2009: 464-469 [3] 周能兵, 王亚斌, 王强. 地磁导航技术研究进展综述[J]. 导航定位学报, 2018, 6(2): 15-19ZHOU Nengbing, WANG Yabin, WANG Qiang. A brief review of geomagnetic navigation technology[J]. Journal of Navigation and Positioning, 2018, 6(2): 15-19 [4] 周军, 葛致磊, 施桂国, 等. 地磁导航发展与关键技术[J]. 宇航学报, 2008, 29(5): 1467-1472 doi: 10.3873/j.issn.1000-1328.2008.05.001ZHOU Jun, GE Zhilei, SHI Guiguo, et al. Key technique and development for geomagnetic navigation[J]. Journal of Astronautics, 2008, 29(5): 1467-1472 doi: 10.3873/j.issn.1000-1328.2008.05.001 [5] CUI F, GAO D, ZHENG J H. Magnetometer-based orbit determination via fast reconstruction of three-dimensional decoupled geomagnetic field model[J]. Journal of Spacecraft and Rockets, 2021, 58(5): 1374-1386 doi: 10.2514/1.A34939 [6] CHEN B, YUAN J H, NI Z, et al. Chinese geomagnetic reference field 2020 by the revised surface spline method[J]. Applied Sciences, 2022, 12(5): 2297 doi: 10.3390/app12052297 [7] XU N H, WANG L H, WU T, et al. An innovative PSO-ICCP matching algorithm for geomagnetic navigation[J]. Measurement, 2022, 193: 110958 doi: 10.1016/j.measurement.2022.110958 [8] CUI F, GAO D, ZHENG J H. Magnetometer-based autonomous orbit determination via a measurement differencing extended Kalman filter during geomagnetic storms[J]. Aircraft Engineering and Aerospace Technology, 2018, 92(3): 428-439 [9] 崔峰. 基于量测差分与模型重构和补偿的地磁导航方法研究[D]. 中国科学院大学(中国科学院国家空间科学中心), 2021CUI Feng. Research for geomagnetic navigation method based on magnetometer difference measurements and model reconstruction & compensation[D]. University of Chinese Academy of Sciences (National Space Science Center, the Chinese Academy of Sciences), 2021 [10] 高东, 张涛, 崔峰, 等. 近地卫星地磁导航发展与高精度地磁导航研究[C]//第二届中国空天安全会议论文集. 大连: 中国指挥与控制学会空天安全平行系统专业委员会, 2017: 438-445GAO Dong, ZHANG Tao, CUI Feng, et al. Research on the development of near-Earth satellite geomagnetic navigation and high-precision geomagnetic navigation[C]//The 2nd China Air and Space Security Conference. Dalian, 2017: 438-445 [11] 于向前, 刘斯, 肖池阶, 等. 基于椭球拟合的三轴磁强计两步校准法[J]. 仪表技术与传感器, 2021(2): 52-56YU Xiangqian, LIU Si, XIAO Chijie, et al. Two-step calibration of tri-axial magnetometer based on ellipsoid fitting[J]. Instrument Technique and Sensor, 2021(2): 52-56 [12] 肖琦, 刘胜利, 孟立飞, 等. 电磁监测卫星磁洁净控制方法研究[J]. 装备环境工程, 2018, 15(6): 78-81XIAO Qi, LIU Shengli, MENG Lifei, et al. Magnetic cleanliness control methods of seismo-electromagnetic satellite[J]. Equipment Environmental Engineering, 2018, 15(6): 78-81 [13] 寇义民, 夏红伟, 刘睿, 等. 一种地磁导航中的低频电磁干扰场分离方法[J]. 哈尔滨工业大学学报, 2011, 43(7): 32-37 doi: 10.11918/j.issn.0367-6234.2011.07.007KOU Yimin, XIA Hongwei, LIU Rui, et al. Method for separation of low-frequency electromagnetic interference in geomagnetic navigation systems[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 32-37 doi: 10.11918/j.issn.0367-6234.2011.07.007 [14] 董晓芬, 陈国光, 田晓丽, 等. 基于CEEMDAN阈值滤波的磁场信号去噪模型[J]. 传感技术学报, 2021, 34(7): 919-925 doi: 10.3969/j.issn.1004-1699.2021.07.011DONG Xiaofen, CHEN Guoguang, TIAN Xiaoli, et al. Denoising model of magnetic field signal based on CEEMDAN threshold filtering[J]. Chinese Journal of Sensors and Actuators, 2021, 34(7): 919-925 doi: 10.3969/j.issn.1004-1699.2021.07.011 [15] 赵塔, 朱小宁, 程德福, 等. 水下地磁导航技术中的地磁场空间差分测量方法[J]. 吉林大学学报:工学版, 2017, 47(1): 316-322ZHAO Ta, ZHU Xiaoning, CHENG Defu, et al. Geomagnetic field spatial difference measuring method for underwater geomagnetic navigation technology[J]. Journal of Jilin University: Engineering and Technology Edition, 2017, 47(1): 316-322 [16] 赵塔, 陈雨薇, 周志坚, 等. 一种水下载体干扰磁场的空间差分补偿方法[J]. 电机与控制学报, 2016, 20(3): 71-76ZHAO Ta, CHEN Yuwei, ZHOU Zhijian, et al. Spatial difference compensation method of underwater vehicle interference magnetic field[J]. Electric Machines and Control, 2016, 20(3): 71-76 [17] 徐涛, 温东, 孙晓磊. 基于加速度计和磁强计的方位测量与校正技术研究[J]. 仪器仪表学报, 2009, 30(10): 2018-2022XU Tao, WEN Dong, SUN Xiaolei. Research on azimuth measurement and correction technique with accelerometer and magnetometer[J]. Chinese Journal of Scientific Instrument, 2009, 30(10): 2018-2022 [18] ZHOU Y K, HUANG G, ZHANG X Y. Geomagnetic sensor noise reduction for improving calibration compensation accuracy based on improved HHT algorithm[J]. IEEE Sensors Journal, 2019, 19(24): 12096-12104 doi: 10.1109/JSEN.2019.2940298 [19] CONSTANTINESCU O D, AUSTER H U, DELVA M, et al. Maximum-variance gradiometer technique for removal of spacecraft-generated disturbances from magnetic field data[J]. Geoscientific Instrumentation, Methods and Data Systems, 2020, 9(2): 451-469 doi: 10.5194/gi-9-451-2020 [20] XU X, HUANG L, LIU X J, et al. DeepMAD: deep learning for magnetic anomaly detection and denoising[J]. IEEE Access, 2020, 8: 121257-121266 doi: 10.1109/ACCESS.2020.3006795 [21] 杨云涛, 石志勇, 关贞珍, 等. 一种基于磁偶极子磁场分布理论的磁场干扰补偿方法[J]. 兵工学报, 2008, 29(12): 1485-1491YANG Yuntao, SHI Zhiyong, GUAN Zhenzhen, et al. A magnetic disturbance compensation method based on magnetic dipole magnetic field distributing theory[J]. Acta Armamentarii, 2008, 29(12): 1485-1491 [22] 金煌煌, 庄志洪, 付梦印, 等. 最简多磁偶极子等效建模方法[J]. 系统工程与电子技术, 2021, 43(8): 2066-2075JIN Huanghuang, ZHUANG Zhihong, FU Mengyin, et al. Modeling method using simplest multiple magnetic dipoles equivalence[J]. Systems Engineering and Electronics, 2021, 43(8): 2066-2075 [23] 李季. 地磁测量中载体干扰磁场特性及补偿方法研究[D]. 长沙: 国防科学技术大学, 2013LI Ji. Study on the characteristics and compensation method of vehicle interferential magnetic field in geomagnetic measurement[D]. Changsha: National University of Defense Technology, 2013 [24] 孙浩, 赵伟. 磁传感器阵列技术及其应用[J]. 电测与仪表, 2020, 57(9): 1-7SUN Hao, ZHAO Wei. Technical characteristics and applications of magnetic sensor array[J]. Electrical Measurement & Instrumentation, 2020, 57(9): 1-7 [25] 陈路昭, 冯永强, 郭瑞杰, 等. 地磁背景下基于传感器阵列的磁偶极子目标跟踪方法[J]. 电子与信息学报, 2020, 42(3): 573-581CHEN Luzhao, FENG Yongqiang, GUO Ruijie, et al. Magnetic dipole object tracking algorithm based on magnetometer array in geomagnetic background[J]. Journal of Electronics & Information Technology, 2020, 42(3): 573-581 -
-





 朱明慧 女, 1997年7月出生于河北省保定市. 现为中国科学院国家空间科学中心博士生, 主要研究方向为运动载体平台磁干扰估计技术研究等. E-mail:
朱明慧 女, 1997年7月出生于河北省保定市. 现为中国科学院国家空间科学中心博士生, 主要研究方向为运动载体平台磁干扰估计技术研究等. E-mail: 
 下载:
下载: