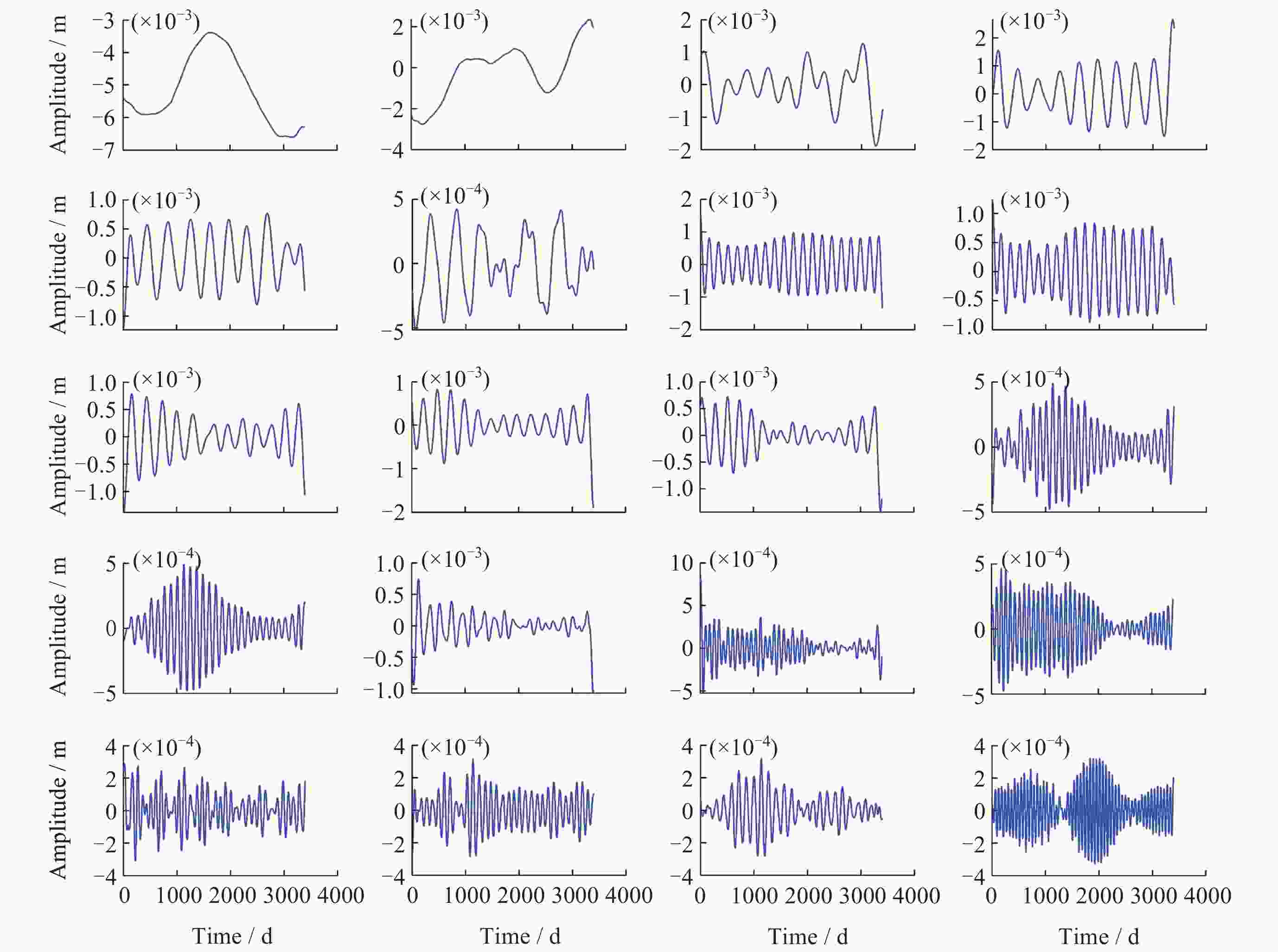
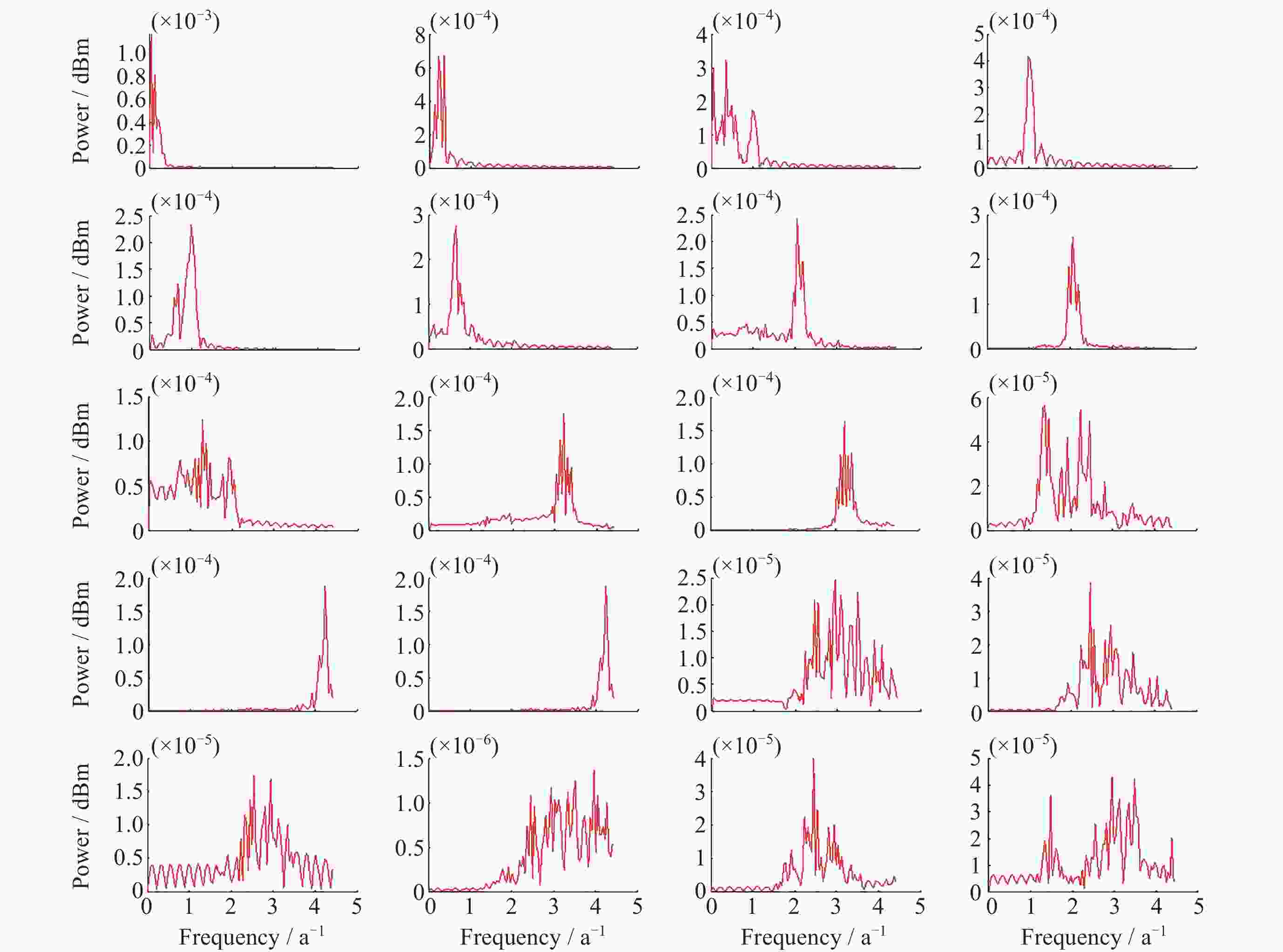
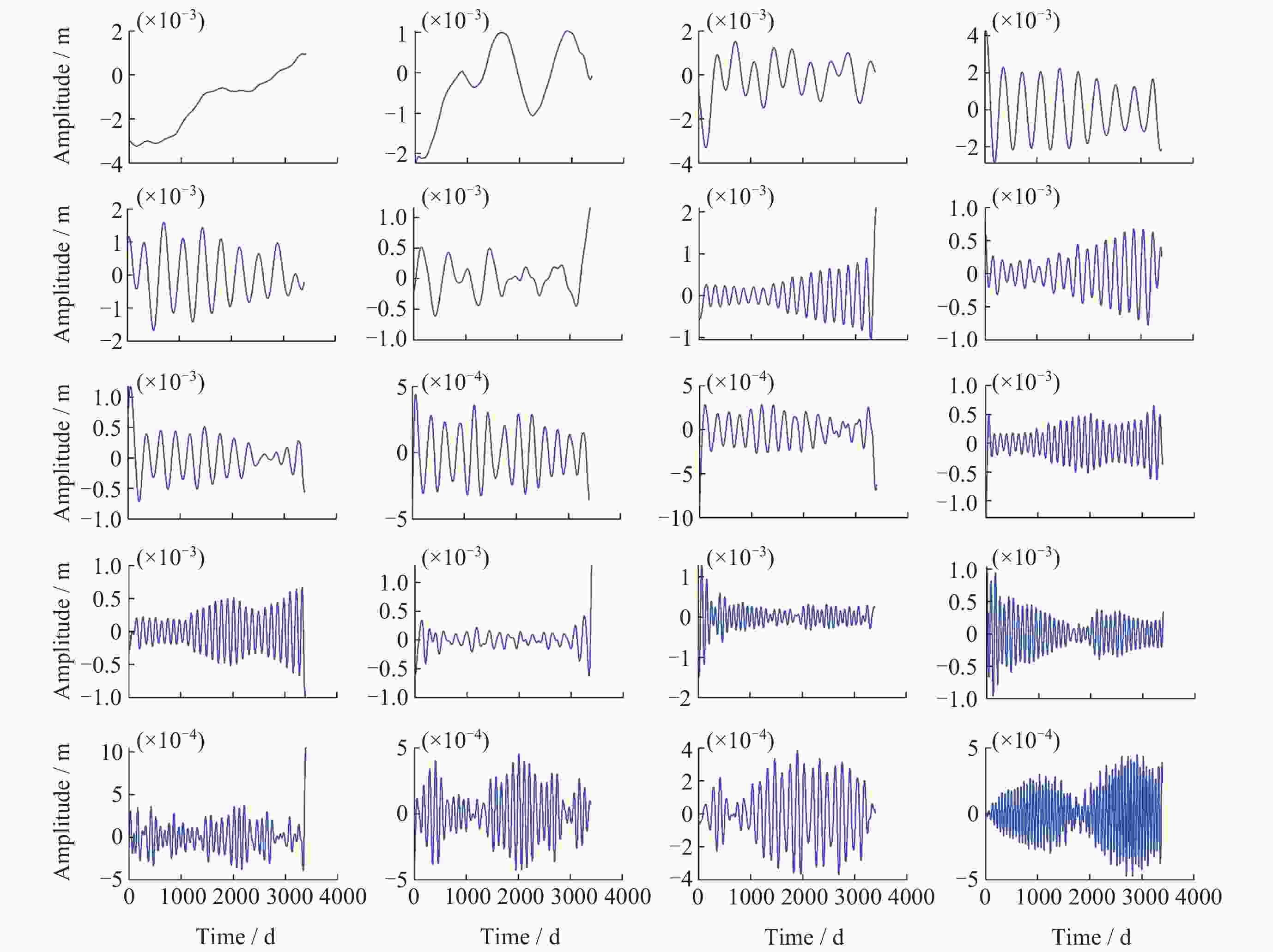
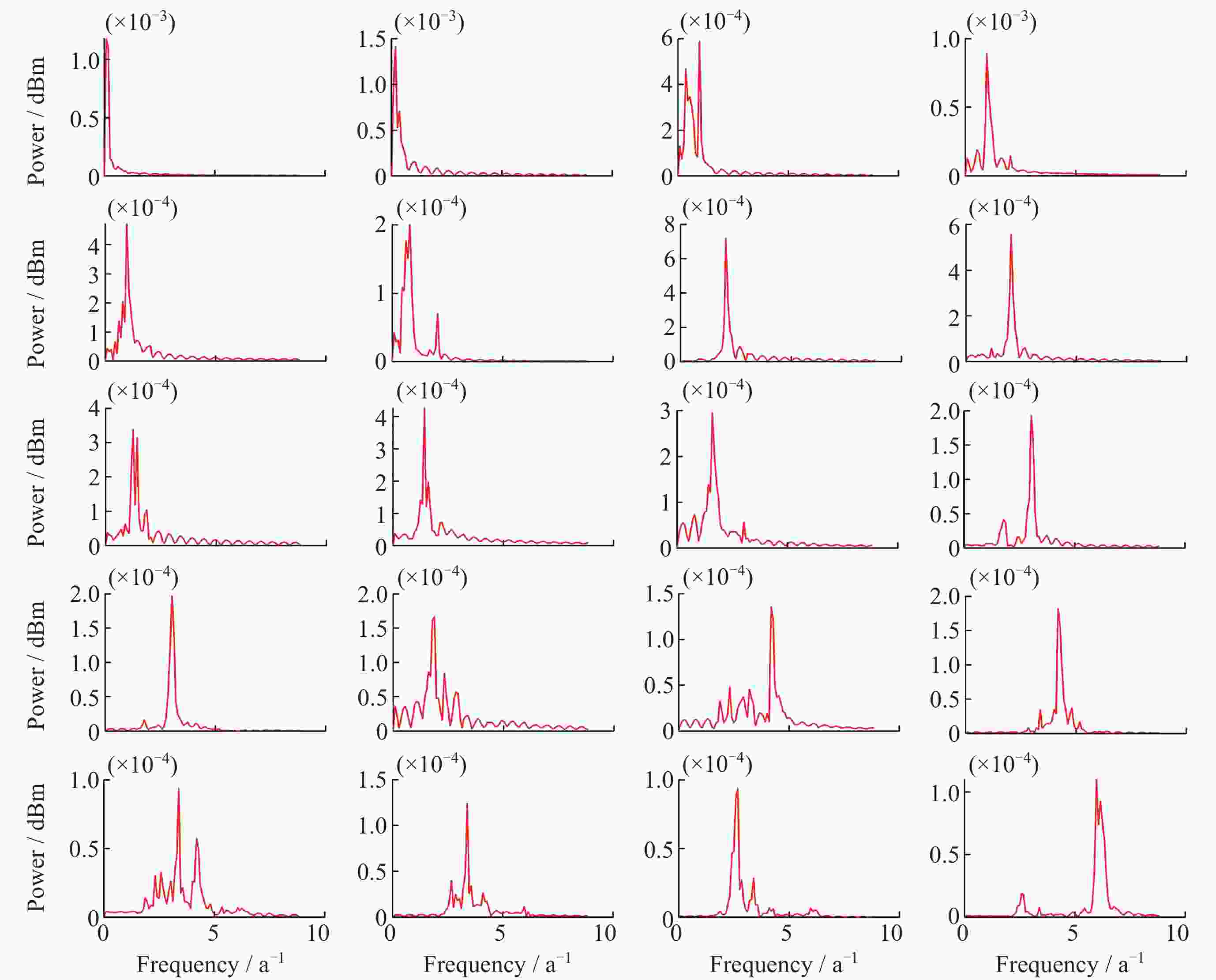
基于MSSA算法的西北地区GNSS坐标时间序列共模误差分析

梁斌; 于明雪

doi:10.11728/cjss2025.04.2024-0072

基于MSSA算法的西北地区GNSS坐标时间序列共模误差分析

doi: 10.11728/cjss2025.04.2024-0072 cstr: 32142.14.cjss.2024-0072

梁斌^1,,
于明雪^2,

1.
中国地震局第一监测中心　天津　300000
2.
兰州交通大学测绘与地理信息学院　兰州　730000

基金项目: 中国地震局第一监测中心科技主任基金项目资助(FMC202307)

详细信息

作者简介:

梁斌　男, 1994年12月出生于山东省青岛市, 现为中国地震局一测工程师, 主要研究方向为GNSS数据处理分析研究. E-mail: skliangbin@126.com

于明雪　女, 1997年10月出生于黑龙江省绥化市, 现为信德智图工程师, 主要研究方向为土地资源利用分析研究. E-mail: 1171227275@126.com

中图分类号: P258
计量
- 文章访问数: 182
- HTML全文浏览量: 31
- PDF下载量: 42
- 被引次数:
  0(来源:Crossref)
  
  0(来源:其他)
出版历程
- 收稿日期: 2024-05-29
- 修回日期: 2024-11-01
- 网络出版日期: 2024-11-02

Common Mode Error Analysis of GNSS Coordinate Time Series in Northwest China Based on MSSA Algorithm

LIANG Bin^1
,,
YU Mingxue^2
,

1.
The First Monitoring Center of China Earthquake Administration, Tianjin 300000
2.
College of Surveying and Geographic Information, Lanzhou Jiaotong University, Lanzhou 730000

摘要

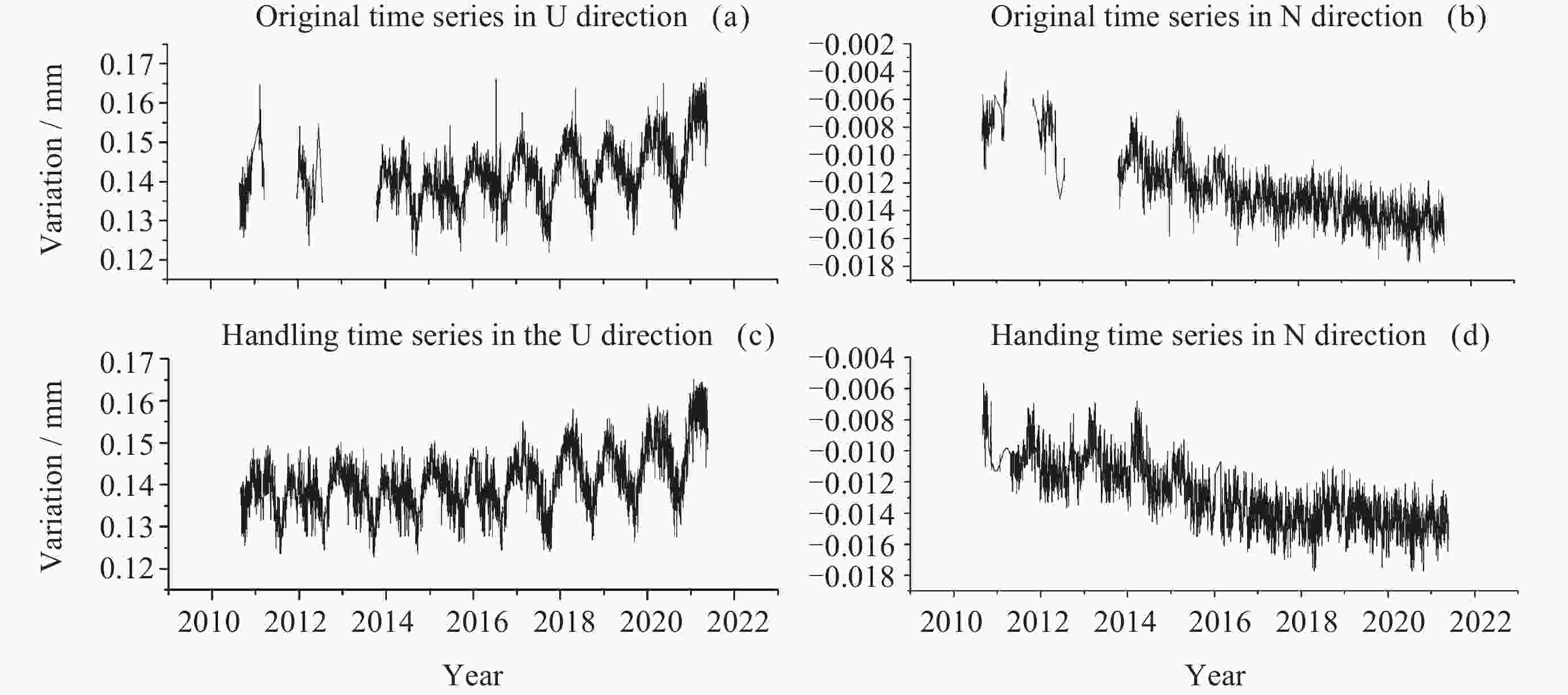
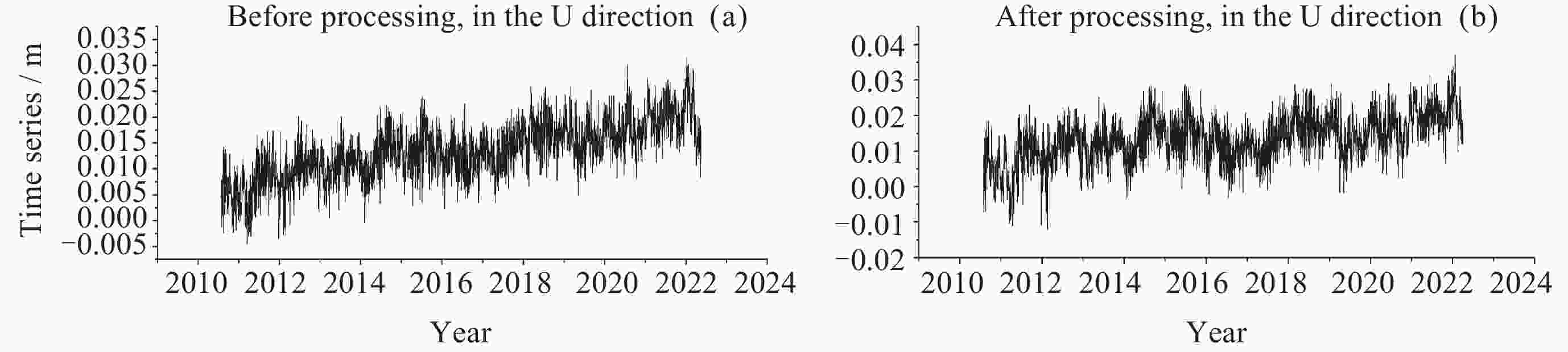
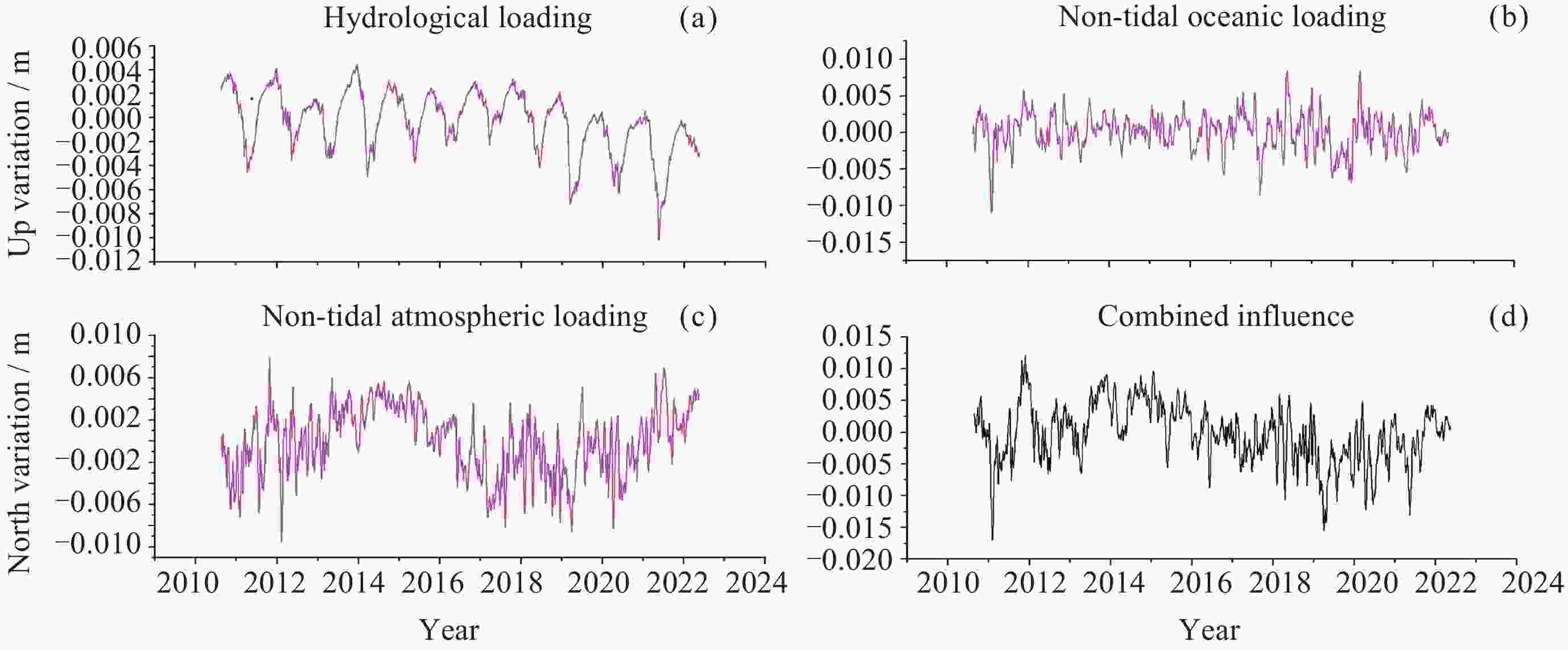
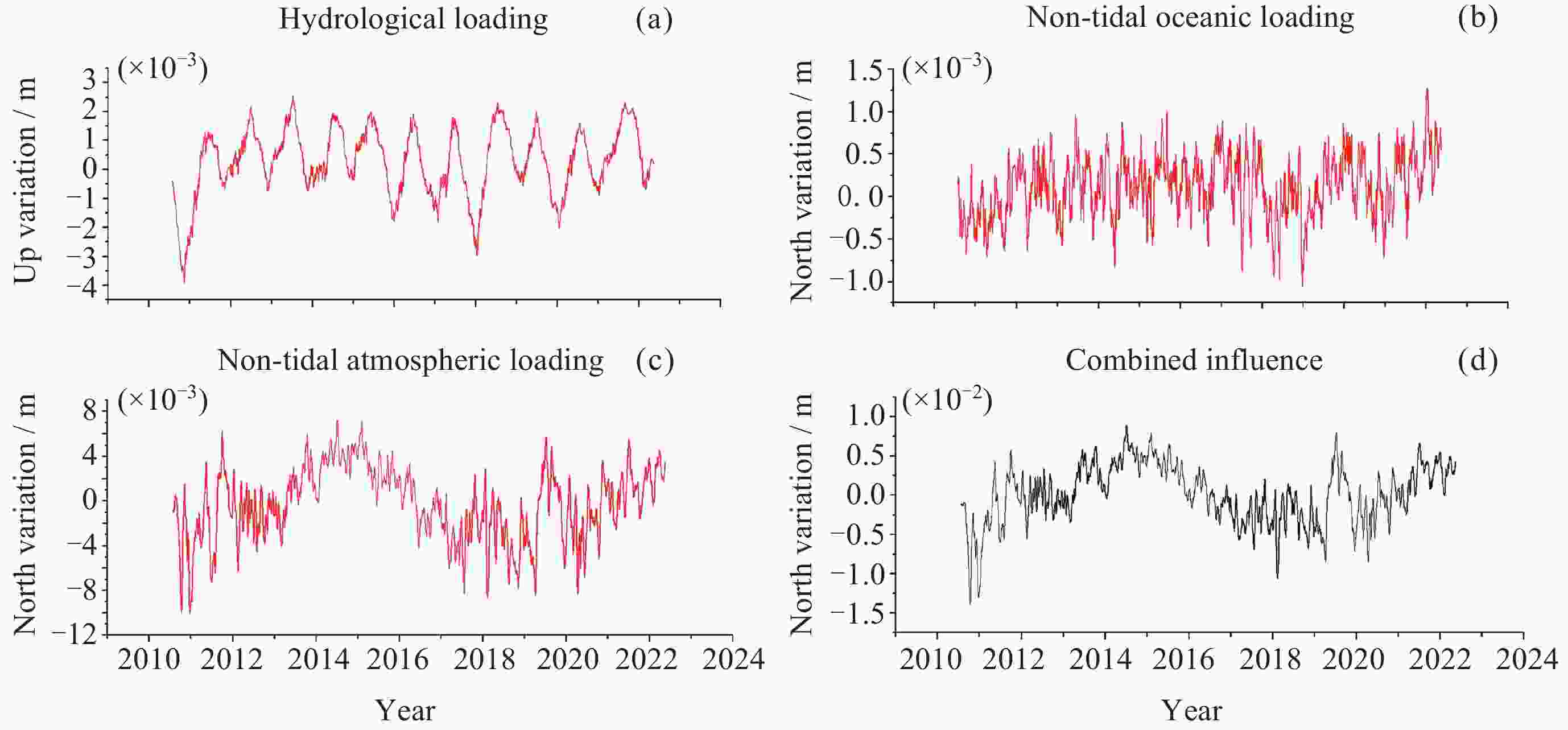
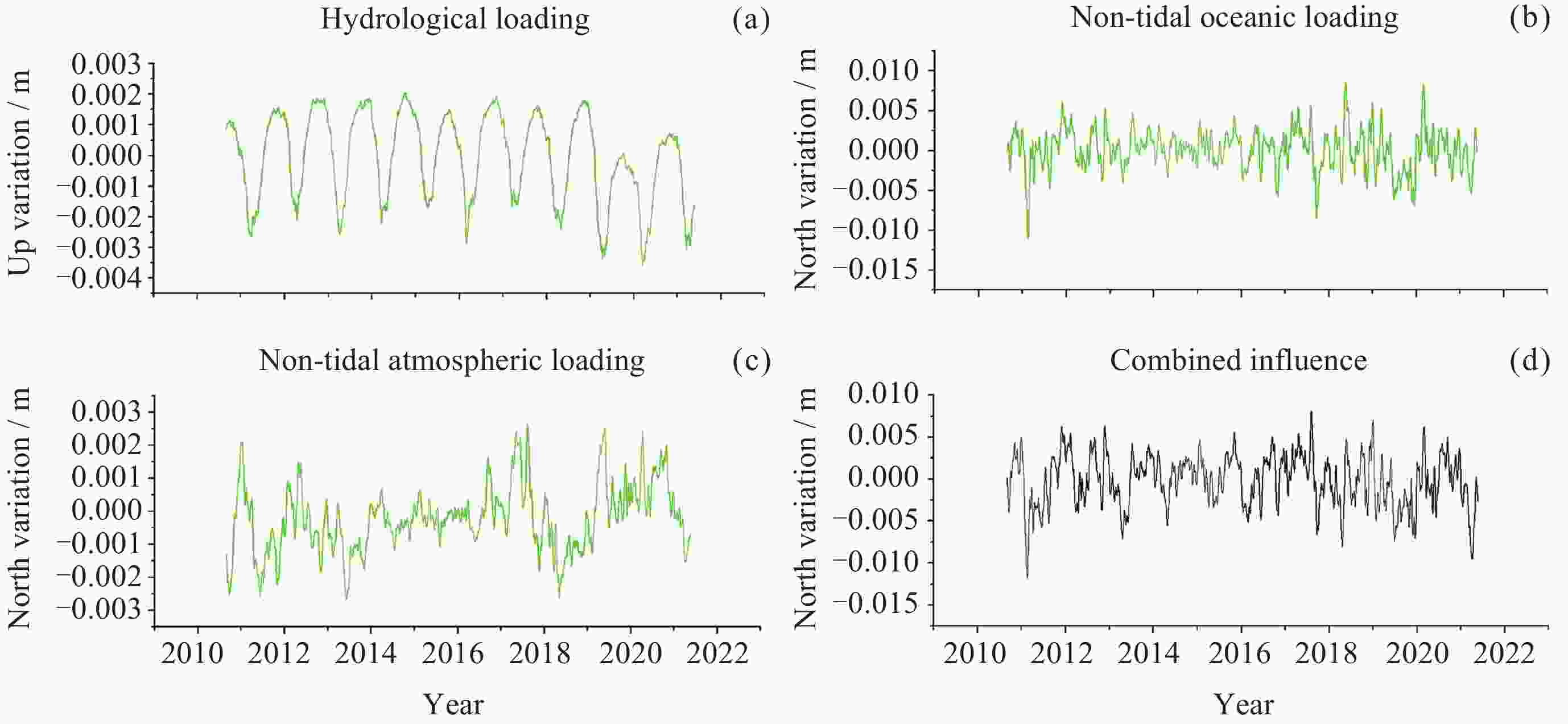
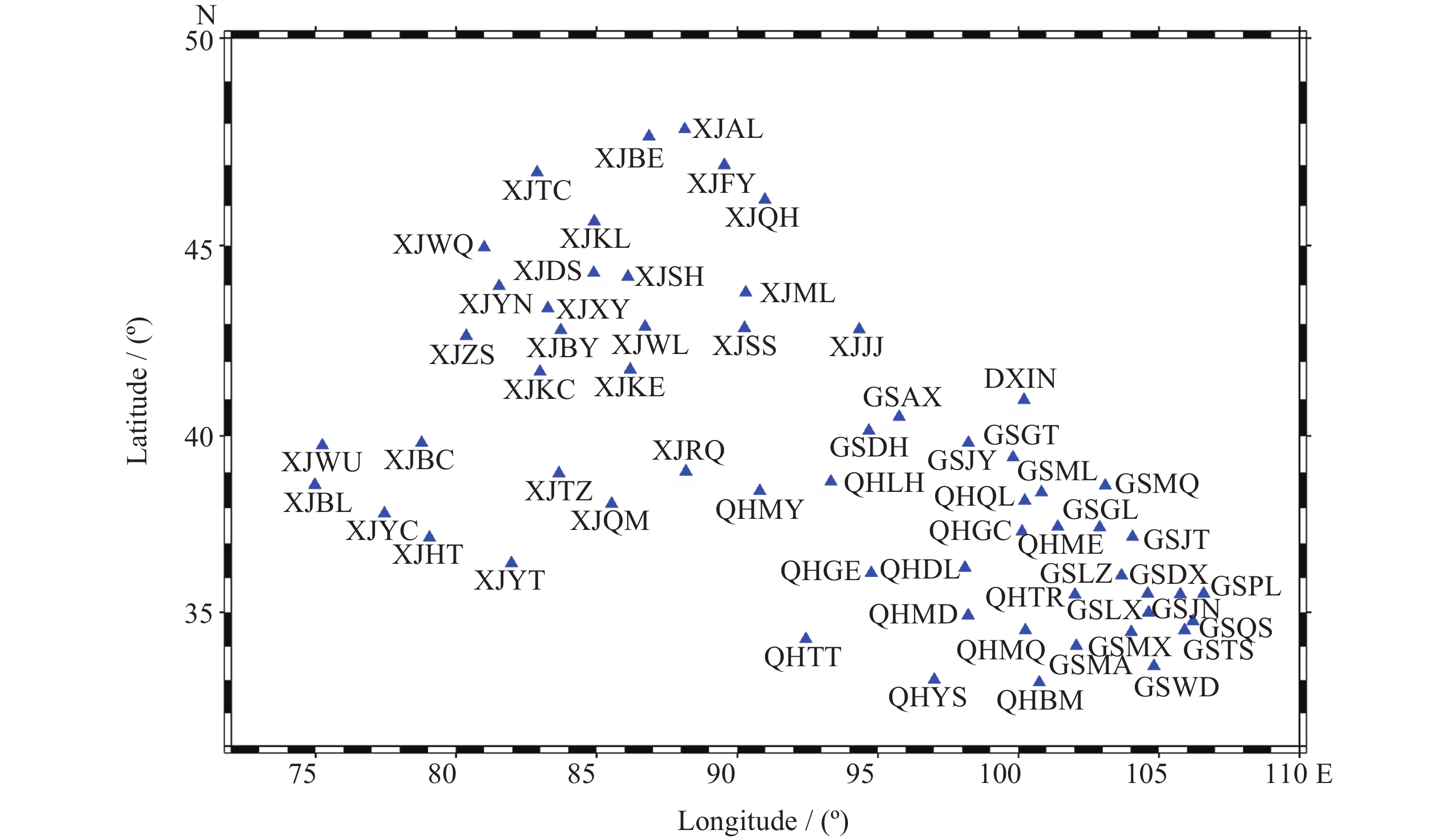
摘要: 针对西北地区新疆、甘肃、青海全球导航卫星系统(GNSS)垂向坐标时间序列的共模误差分析研究不够全面、深入这一问题, 以MSSA算法为理论基础, 对新疆、甘肃、青海61个站点进行数据预处理以提高数据的精度与完整性, 在此基础上提取分析该区域GNSS坐标时间序列中的共模误差, 并进行周期性探测分析, 将提取的共模误差(CME)与水文荷载(NTOL)、非潮汐大气荷载(NTAL)以及非潮汐海洋荷载(HYDL)引起的位移时间序列进行相关性分析以探究共模误差的特征性来源. 对比站点共模误差剔除前后序列, 结果表明残差标准差平均精度提高27.5%, 测站减少幅度最大达到66.7%, 精度提高效果显著; 分析结果得到该区域共模误差受到三种地表质量荷载影响显著程度从高到低分别为水文荷载、非潮汐大气荷载、非潮汐海洋荷载. 通过对共模误差的提取分析以及误差特征来源研究可以进一步提高西北地区GNSS坐标时间序列精度, 以更好地为地震位移、地壳形变研究提供更高精度数据支持.
- 西北地区 /
- 共模误差 /
- GNSS /
- 周期性探测
Abstract: Aiming at the problem that the common mode error analysis of the vertical coordinate time series of the Global Navigation Satellite System (GNSS) in Northwest China is not comprehensive and in-depth, the MSSA algorithm is used as the theoretical basis to preprocess the data of 61 stations in the three northwestern provinces (Xinjiang, Gansu, Qinghai) to improve the accuracy and integrity of the data, and on this basis, the common mode error of GNSS coordinate time series in the region is extracted and analyzed. The characteristic source of the Common Mode Error (CME) was investigated by correlation analysis between the extracted CME and the displacement time series caused by Hydrologic Load (HYDL), Non-Tidal Atmospheric Load (NTAL) and Non-Tidal Ocean Load (NTOL). Compared with the sequence before and after the removal of the common mode error, the average accuracy of the residual standard deviation is increased by 27.5%, and the maximum reduction of the station is reduced by 66.7%. The results show that the common mode error in this region is significantly affected by three kinds of surface mass loads: hydrologic load, non-tidal atmospheric load and non-tidal ocean load. Through the extraction and analysis of common mode errors and the research on the source of error characteristics, the GNSS coordinate time series accuracy of the three northwestern provinces can be further improved, so as to provide higher precision data support for seismic displacement and crustal deformation research.
- Northwest China /
- Common mode error /
- GNSS /
- Periodic detection

HTML全文

图 1 西北地区GNSS连续站分布

Figure 1. Distribution of GNSS continuous stations in the northwestern China region

下载: 全尺寸图片幻灯片

图 2 预处理前后对比分析

Figure 2. Comparative analysis before and after pretreatment

下载: 全尺寸图片幻灯片

图 3 共模误差剔除前后对比

Figure 3. Comparison before and after common-mode error removal

下载: 全尺寸图片幻灯片

图 4 GSQS站共模误差信号分离结果

Figure 4. GSQS station periodic separation results of common-mode error signals

下载: 全尺寸图片幻灯片

图 5 GSQS站周期性共模误差检测结果

Figure 5. GSQS station Periodic detection results of common-mode errors

下载: 全尺寸图片幻灯片

图 6 QHMY站共模误差信号分离结果

Figure 6. QHMY station separation results of common-mode error signals

下载: 全尺寸图片幻灯片

图 7 QHMY站周期性共模误差检测结果

Figure 7. QHMY station Periodic detection results of common-mode errors

下载: 全尺寸图片幻灯片

图 8 XJZS站共模误差信号分离结果

Figure 8. XJZS station periodic separation results of common-mode error signals

下载: 全尺寸图片幻灯片

图 9 QHMY站周期性共模误差检测结果

Figure 9. XJZS station detection results of common-mode errors

下载: 全尺寸图片幻灯片

图 10 GSQH站点荷载分析

Figure 10. GSQH site load analysis

下载: 全尺寸图片幻灯片

图 12 XJZS站点荷载分析

Figure 12. XJZS site load analysis

下载: 全尺寸图片幻灯片

图 11 QHMY站点荷载分析

Figure 11. QHMY site load analysis

下载: 全尺寸图片幻灯片

表 1 共模误差剔除前后振幅对比

Table 1. Amplitude comparison before and after common-mode error removal

测站	状态	最大值/m	最小值/m	平均值/m	标准差/m	测站	状态	最大值/m	最小值/m	平均值/m	标准差/m
GSAX	改正前	0.008	–0.022	–0.007	0.015	QHTT	改正前	0.029	–0.004	0.012	0.016
GSAX	改正后	0.005	–0.016	–0.003	0.011	QHTT	改正后	0.011	–0.004	0.005	0.007

GSDH	改正前	0.013	–0.017	–0.003	0.015	QHYS	改正前	0.017	–0.012	0.006	0.019
GSDH	改正后	0.011	–0.014	–0.002	0.009	QHYS	改正后	0.009	–0.005	0.003	0.007

GSDX	改正前	0.021	–0.025	0.002	0.023	XJAL	改正前	0.077	–0.021	0.021	0.049
GSDX	改正后	0.016	–0.017	–0.001	0.019	XJAL	改正后	0.021	–0.013	0.011	0.021

GSDL	改正前	0.006	–0.007	0.001	0.003	XJBC	改正前	0.022	–0.028	–0.008	0.021
GSDL	改正后	0.005	–0.007	0.001	0.002	XJBC	改正后	0.013	–0.011	–0.004	0.013

GSDT	改正前	0.005	–0.008	0.008	0.007	XJBE	改正前	0.023	–0.011	0.005	0.018
GSDT	改正后	0.003	–0.005	0.006	0.005	XJBE	改正后	0.011	–0.007	0.003	0.006

GSJN	改正前	0.035	–0.029	0.008	0.032	XJBY	改正前	0.036	–0.009	0.012	0.024
GSJN	改正后	0.021	–0.017	0.005	0.015	XJBY	改正后	0.015	–0.005	0.007	0.015

GSJT	改正前	0.029	–0.021	0.006	0.024	XJDS	改正前	0.016	–0.023	–0.006	0.019
GSJT	改正后	0.015	–0.017	0.004	0.019	XJDS	改正后	0.007	–0.011	–0.003	0.014

GSJY	改正前	0.021	–0.014	0.003	0.017	XJFY	改正前	0.017	–0.012	–0.003	0.018
GSJY	改正后	0.011	–0.007	0.002	0.011	XJFY	改正后	0.009	–0.013	–0.001	0.013

GSLY	改正前	0.044	–0.031	–0.009	0.037	XJHT	改正前	0.027	–0.009	0.004	0.018
GSLY	改正后	0.017	–0.012	–0.005	0.015	XJHT	改正后	0.011	–0.004	0.002	0.014

GSLZ	改正前	0.014	–0.04	–0.013	0.027	XJJJ	改正前	0.006	–0.031	–0.011	0.018
GSLZ	改正后	0.007	–0.017	–0.005	0.017	XJJJ	改正后	0.002	–0.015	–0.005	0.014

GSMA	改正前	0.014	–0.026	0.004	0.011	XJKC	改正前	0.004	–0.032	–0.015	0.018
GSMA	改正后	0.007	–0.017	0.004	0.007	XJKC	改正后	0.003	–0.015	–0.007	0.013

GSMI	改正前	0.015	–0.013	0.002	0.014	XJKE	改正前	0.018	–0.033	–0.012	0.021
GSMI	改正后	0.007	–0.005	0.001	0.005	XJKE	改正后	0.011	–0.015	–0.009	0.015

GSML	改正前	0.017	–0.026	0.011	0.019	XJKL	改正前	0.015	–0.001	0.055	0.075
GSML	改正后	0.011	–0.017	0.004	0.007	XJKL	改正后	0.009	–0.001	0.027	0.054

GSMQ	改正前	0.023	–0.034	0.005	0.028	XJML	改正前	0.011	–0.027	–0.008	0.019
GSMQ	改正后	0.011	–0.016	0.001	0.027	XJML	改正后	0.007	–0.008	–0.007	0.013

GSMX	改正前	0.013	–0.026	–0.004	0.019	XJQH	改正前	0.026	–0.009	0.005	0.016
GSMX	改正后	0.005	–0.013	–0.001	0.007	XJQH	改正后	0.011	0.003	0.002	0.011

GSPL	改正前	0.031	–0.034	0.002	0.022	XJQM	改正前	0.017	–0.021	–0.001	0.021
GSPL	改正后	0.015	–0.017	0.001	0.013	XJQM	改正后	0.009	–0.016	0.002	0.017

GSTS	改正前	0.073	–0.016	0.022	0.024	XJRQ	改正前	0.018	–0.015	0.002	0.016
GSTS	改正后	0.024	–0.009	0.011	0.021	XJRQ	改正后	0.011	–0.009	0.002	0.014

GSQS	改正前	0.034	–0.031	0.007	0.013	XJSH	改正前	0.015	–0.024	0.005	0.019
GSQS	改正后	0.017	–0.019	0.002	0.009	XJSH	改正后	0.012	–0.015	0.004	0.015
GSWD	改正前	0.024	–0.032	–0.009	0.018	XJSS	改正前	0.002	–0.011	–0.007	0.016
GSWD	改正后	0.011	–0.017	–0.005	0.015	XJSS	改正后	0.002	–0.009	–0.005	0.07

DXIN	改正前	0.059	–0.029	0.014	0.014	XJTC	改正前	0.032	–0.013	0.011	0.022
DXIN	改正后	0.018	–0.012	0.005	0.013	XJTC	改正后	0.023	–0.007	0.006	0.017

QHBM	改正前	0.034	–0.024	0.002	0.031	XJTZ	改正前	0.022	–0.029	–0.001	0.025
QHBM	改正后	0.013	–0.007	–0.001	0.013	XJTZ	改正后	0.019	–0.014	0.002	0.019

QHDL	改正前	0.021	–0.022	0.009	0.020	XJWL	改正前	0.025	–0.016	0.003	0.02
QHDL	改正后	0.007	–0.013	0.005	0.009	XJWL	改正后	0.013	–0.012	0.001	0.016

QHGC	改正前	0.023	–0.019	0.004	0.017	XJWQ	改正前	0.004	–0.037	–0.018	0.02
QHGC	改正后	0.005	–0.014	0.002	0.013	XJWQ	改正后	0.004	–0.015	–0.009	0.015

QHGE	改正前	0.021	–0.026	0.001	0.023	XJWU	改正前	0.004	–0.038	–0.015	0.02
QHGE	改正后	0.012	–0.013	0.002	0.015	XJWU	改正后	0.003	–0.014	–0.007	0.017

QHLH	改正前	0.066	–0.01	0.017	0.027	XJXY	改正前	0.041	–0.008	0.016	0.024
QHLH	改正后	0.009	0.001	0.011	0.019	XJXY	改正后	0.019	–0.005	0.007	0.019

QHMD	改正前	0.012	–0.019	0.007	0.011	XJYC	改正前	0.027	–0.026	0.001	0.026
QHMD	改正后	0.005	–0.009	0.004	0.005	XJYC	改正后	0.015	–0.013	0.001	0.021

QHME	改正前	0.032	0.001	0.013	0.011	XJYN	改正前	0.063	–0.041	–0.015	0.052
QHME	改正后	0.012	0.001	0.007	0.007	XJYN	改正后	0.017	–0.015	–0.009	0.047

QHMQ	改正前	0.074	–0.026	0.006	0.036	XJYT	改正前	0.008	–0.028	–0.009	0.025
QHMQ	改正后	0.017	–0.011	0.004	0.023	XJYT	改正后	0.007	–0.012	–0.005	0.017

QHMY	改正前	0.014	–0.048	0.006	0.019	XJZS	改正前	0.036	–0.013	0.013	0.025
QHMY	改正后	0.008	–0.021	0.01	0.012	XJZS	改正后	0.015	–0.007	0.007	0.019

QHQL	改正前	0.046	–0.009	0.013	0.028	XJBL	改正前	0.014	–0.021	0.004	0.019
QHQL	改正后	0.014	–0.005	0.008	0.019	XJBL	改正后	0.005	–0.013	0.003	0.013

QHTR	改正前	0.013	–0.093	0.005	0.053
QHTR	改正后	0.005	–0.019	0.003	0.031

下载: 导出CSV

表 2 荷载平均相关性系数

Table 2. Average load correlation coefficient

荷载类别	平均相关性系数/(%)
HYDL	41.2
NTAL	22.1
NTOL	8.9

下载: 导出CSV

参考文献(20)

[1]	YAN J, DONG D N, BÜRGMANN R, et al. Separation of sources of seasonal uplift in China using independent component analysis of GNSS time series[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(11): 11951-11971 doi: 10.1029/2019JB018139
[2]	盛传贞, 甘卫军, 梁诗明, 等. 滇西地区GPS时间序列中陆地水载荷形变干扰的GRACE分辨与剔除[J]. 地球物理学报, 2014, 57(1): 42-52 doi: 10.6038/cjg20140105 SHENG Chuanzhen, GAN Weijun, LIANG Shiming, et al. Identification and elimination of non-tectonic crustal deformation caused by land water from GPS time series in the western Yunnan province based on GRACE observations[J]. Chinese Journal of Geophysics, 2014, 57(1): 42-52 doi: 10.6038/cjg20140105
[3]	廖华, 徐锐, 陈维锋, 等. 汶川地震前后四川区域GPS时序特征演变及统计分析[J]. 地球物理学报, 2013, 56(4): 1237-1245 doi: 10.6038/cjg20130418 LIAO Hua, XU Rui, CHEN Weifeng, et al. Propertyvariation and statistical analysis of Sichuan GPS time series before and after Wenchuan Earthquake[J]. Chinese Journal of Geophysics, 2013, 56(4): 1237-1245 doi: 10.6038/cjg20130418
[4]	杨博, 周伟, 陈阜超, 等. GPS连续站水平位置时间序列共模白噪声识别与估计的欧拉-滤波法[J]. 山东科技大学学报(自然科学版), 2010, 29(3): 26-31,36 YANG Bo, ZHOU Wei, CHEN Fuchao, et al. The Euler-filter algorithm of recognition and estimation on the common mode white noise of time series for horizontal components of GPS continuous observation stations[J]. Journal of Shandong University of Science and Technology (Natural Science Edition), 2010, 29(3): 26-31,36
[5]	杨博, 张风霜, 韩月萍. GPS连续站水平分量时间序列共模误差识别的欧拉-小波法[J]. 大地测量与地球动力学, 2010, 30(3): 100-104 doi: 10.3969/j.issn.1671-5942.2010.03.024 YANG Bo, ZHANG Fengshuang, HAN Yueping. Euler–wavelet method and its application in identification of common–mode error from time sequences of horizontal components of GPS continuous stations[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 100-104 doi: 10.3969/j.issn.1671-5942.2010.03.024
[6]	王梅, 江在森, 侯贺晟. GPS连续站水平位移分量相关性分析[J]. 大地测量与地球动力学, 2010, 30(2): 19-24 doi: 10.3969/j.issn.1671-5942.2010.02.005 WANG Mei, JIANG Zaiden, HOU Hesheng. Correlation analysis of continuous GPS horizontal displacement components[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 19-24 doi: 10.3969/j.issn.1671-5942.2010.02.005
[7]	谢树明, 潘鹏飞, 周晓慧. 大空间尺度GPS网共模误差提取方法研究[J]. 武汉大学学报•信息科学版, 2014, 39(10): 1168-1173 XIE Shuming, PAN Pengfei, ZHOU Xiaohui. Research on common mode error extraction method for large–scale GPS network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1168-1173
[8]	谢树明, 潘鹏飞, 周晓慧. GPS坐标时间序列共模误差空间特性分析[J]. 地理空间信息, 2014, 12(4): 44-45,54 doi: 10.11709/j.issn.1672-4623.2014.04.015 XIE Shuming, PAN Pengfei, ZHOU Xiaohui. Spatial characteristics analysis of common mode error in GPS coordinate time series[J]. Geospatial Information, 2014, 12(4): 44-45,54 doi: 10.11709/j.issn.1672-4623.2014.04.015
[9]	田云锋, 沈正康, 李鹏. 连续GPS观测中的相关噪声分析[J]. 地震学报, 2010, 32(6): 696-704 TIAN Yunfeng, SHEN Zhengkang, LI Peng. Analysis on correlated noise in continuous GPS observations[J]. Acta Seismologica Sinica, 2010, 32(6): 696-704
[10]	TAN W J, CHEN J P, DONG D N, et al. Analysis of the potential contributors to common mode error in Chuandian region of China[J]. Remote Sensing, 2020, 12(5): 751 doi: 10.3390/rs12050751
[11]	王丽红, 鲁杨梅, 邱宝贤. GAMIT软件中不同星历对GPS/BDS数据定位的影响[J]. 海洋测绘, 2022, 42(1): 14-17 doi: 10.3969/j.issn.1671-3044.2022.01.004 WANG Lihong, LU Yangmei, QIU Baoxian. Position affect of GPS/BDS data by GAMIT with different precise ephemeris[J]. Hydrographic Surveying and Charting, 2022, 42(1): 14-17 doi: 10.3969/j.issn.1671-3044.2022.01.004
[12]	何月帆, 聂桂根, 武曙光, 等. 不同版本的GAMIT超短基线数据解算精度分析[J]. 测绘工程, 2021, 30(5): 18-22, 31 HE Yuefan, NIE Guigen, WU Shuguang et al. Ultra–short baseline solution based on different versions of GAMT[J]. Engineering of Surveying and Mapping, 2019, 30(5): 18-22, 31
[13]	姜卫平. GNSS基准站网数据处理方法与应用[M]. 武汉: 武汉大学出版社, 2017 JIANG Weiping. GNSS Reference Station Network Data Processing Method and Application[M]. Wuhan: Wuhan University Press, 2017
[14]	侯增楠, 黄征凯, 王琰, 等. 一种改进WVSSA算法的GNSS时间序列降噪方法[J]. 导航定位学报, 2023, 11(4): 97-103 HOU Zengnan, HUANG Zhengkai, WANG Yan, et al. A noise reduction method for GNSS time series based on improved WVSSA algorithm[J]. Journal of Navigation and Positioning, 2023, 11(4): 97-103
[15]	何月帆. 高精度GPS数据处理及时间序列分析[D]. 西安: 长安大学, 2019 HE Yuefan. High Precision GPS Data Processing and Time Series Analysis[D]. Xi’an: Chang’an University, 2019
[16]	钱炜, 岳建平. MSSA在GPS坐标序列分析中的应用[J]. 测绘通报, 2021(9): 49-52,63 QIAN Wei, YUE Jianping. Application of MSSA in GPS coordinate sequence analysis[J]. Bulletin of Surveying and Mapping, 2021(9): 49-52,63
[17]	李爱国, 平书哑, 郭敏. 利用改进3σ法获得残差序列的共模误差提取[J]. 测绘科学, 2023, 48(7): 72-83 LI Aiguo, PING Shaya, GUO Min. The common mode error extraction of residual series was obtained by improved 3σ method[J]. Science of Surveying and Mapping, 2023, 48(7): 72-83
[18]	YUAN P, LI Z, JIANG W P, et al. Influences of environmental loading corrections on the nonlinear variations and velocity uncertainties for the reprocessed global positioning system height time series of the crustal movement observation network of China[J]. Remote Sensing, 2018, 10(6): 958 doi: 10.3390/rs10060958
[19]	常航. GPS垂向时序中环境负载效应研究[D]. 西安: 长安大学, 2019 CHANG Hang. Research on Environmental Loading Effect in GPS Vertical Time Series[D]. Xi’an: Chang’an University, 2019
[20]	DILL R, DOBSLAW H. Numerical simulations of global-scale high-resolution hydrological crustal deformations[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(9): 5008-5017 doi: 10.1002/jgrb.50353