基于SegRNN的热层大气密度经验模型校准
doi: 10.11728/cjss2025.06.2024-0179 cstr: 32142.14.cjss.2024-0179
-
曹庆鹏 男, 1998年6月出生于黑龙江省牡丹江市, 现就读于中山大学人工智能学院计算机技术专业, 主要研究方向为热层大气密度经验模型校准. E-mail: caoqingpengpeng11@126.com -
谷德峰 男, 1980年8月出生, 现为中山大学教授、博导, 人工智能学院副院长, 主要研究方向为低/中/高轨多类卫星及其编队轨道确定, 系统误差建模抑制, 时空序列智能预测. E-mail: gudefeng@mail.sysu.edu.cn
作者简介:
通讯作者:
Calibration of Thermospheric Atmospheric Density Empirical Model Based on SegRNN
-
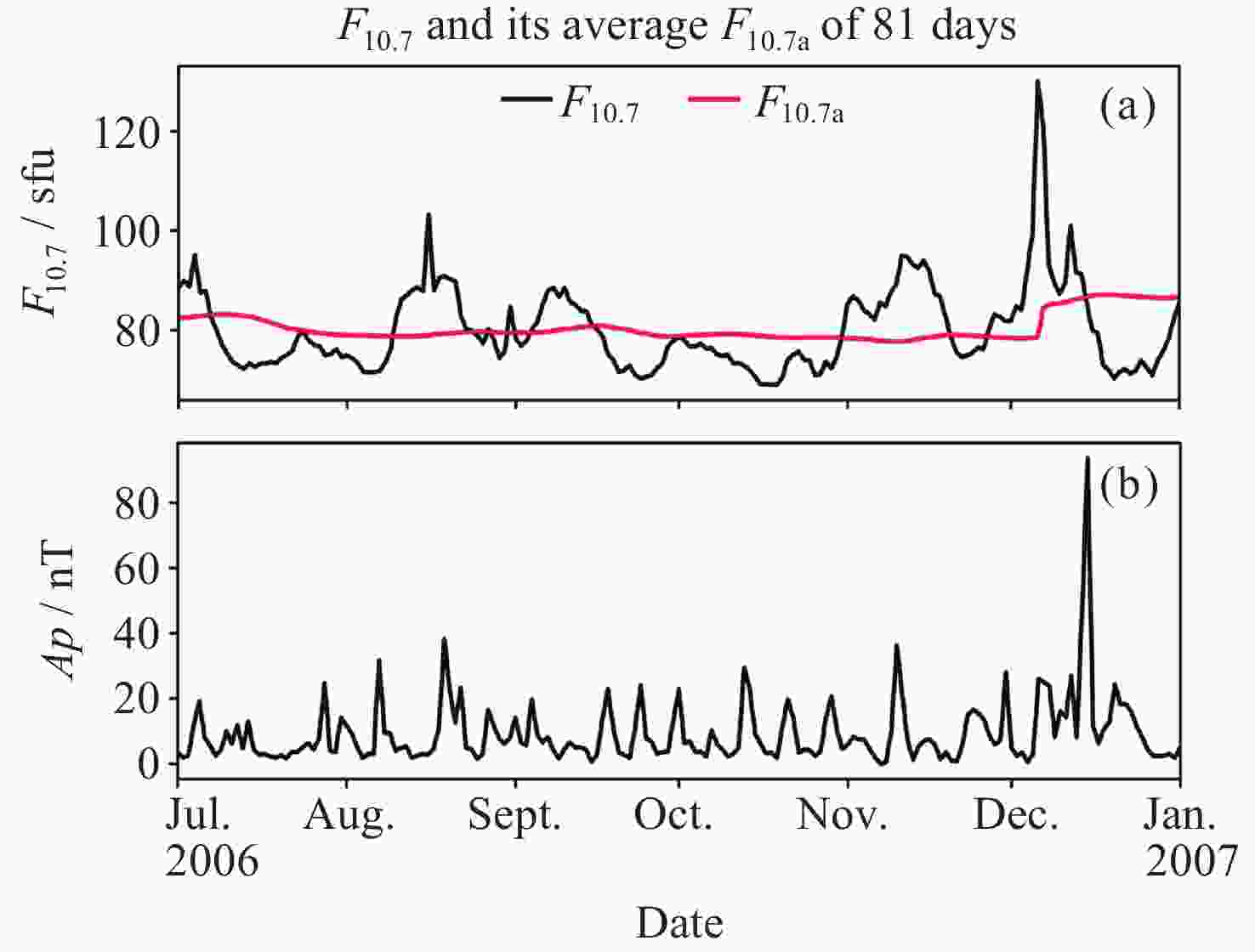
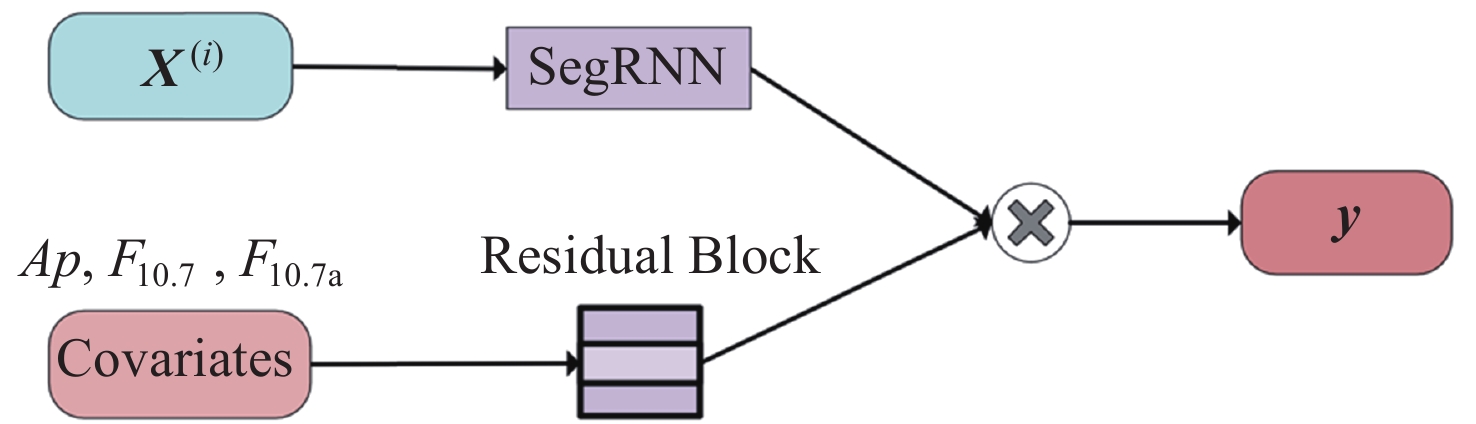
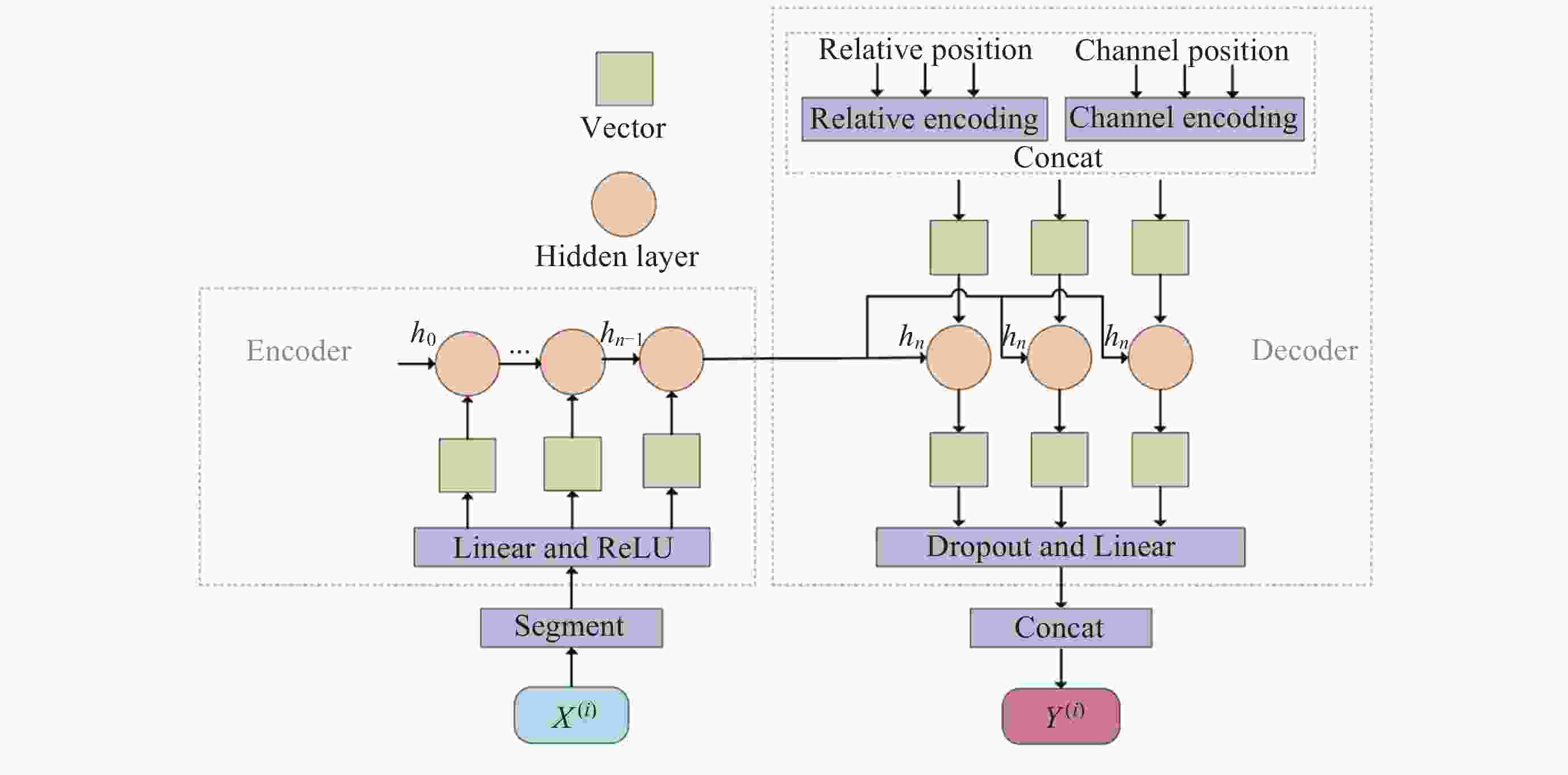
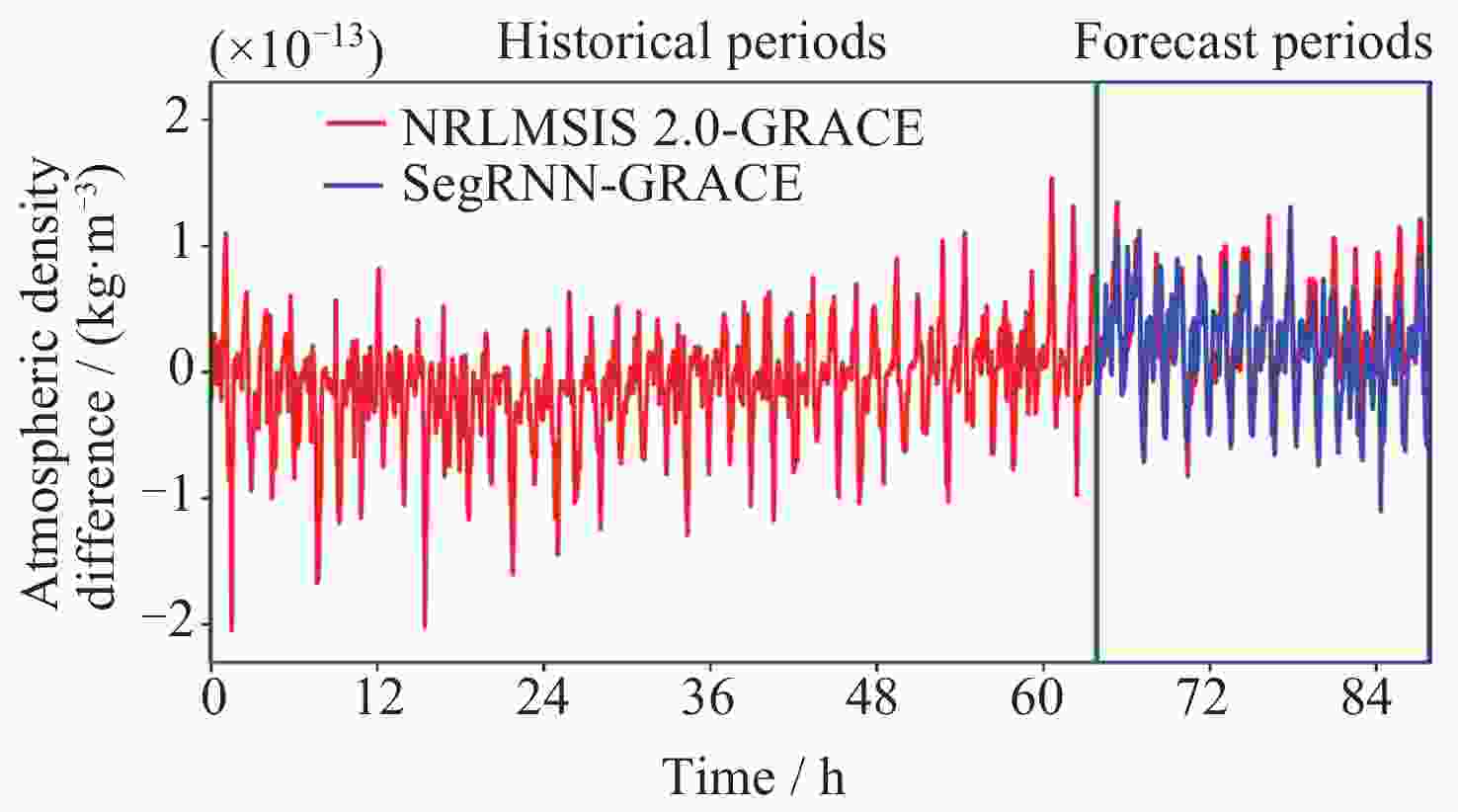
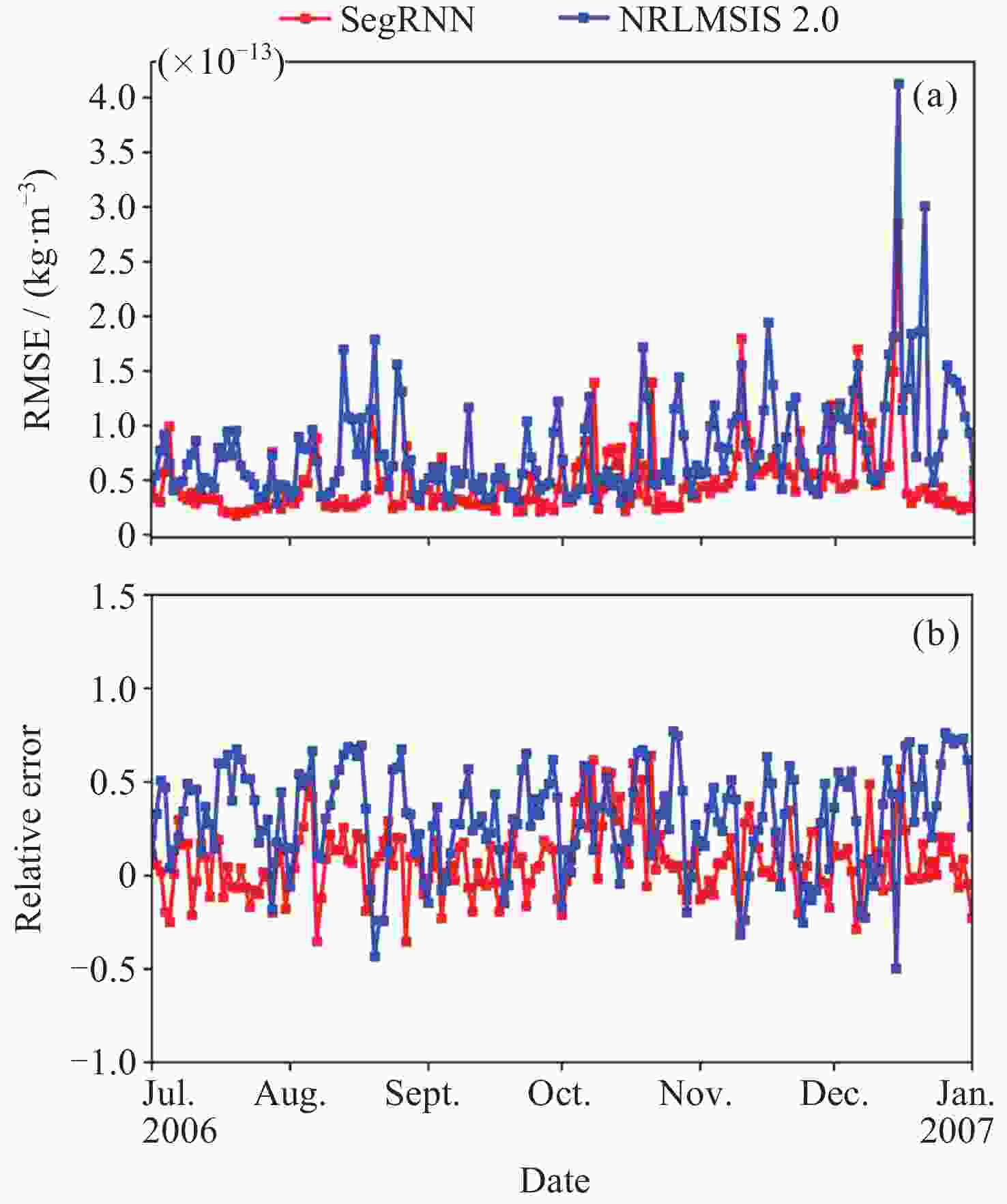
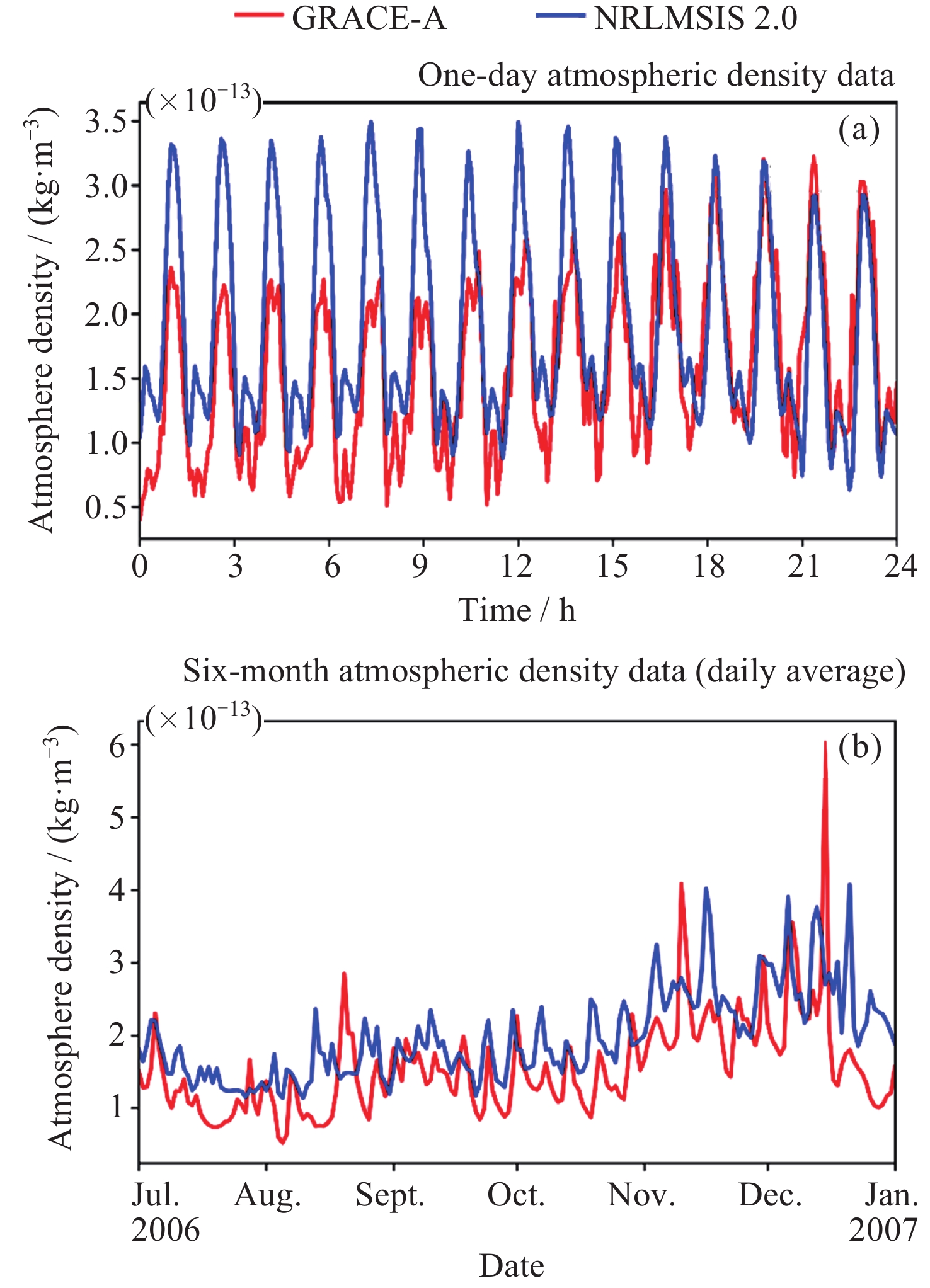
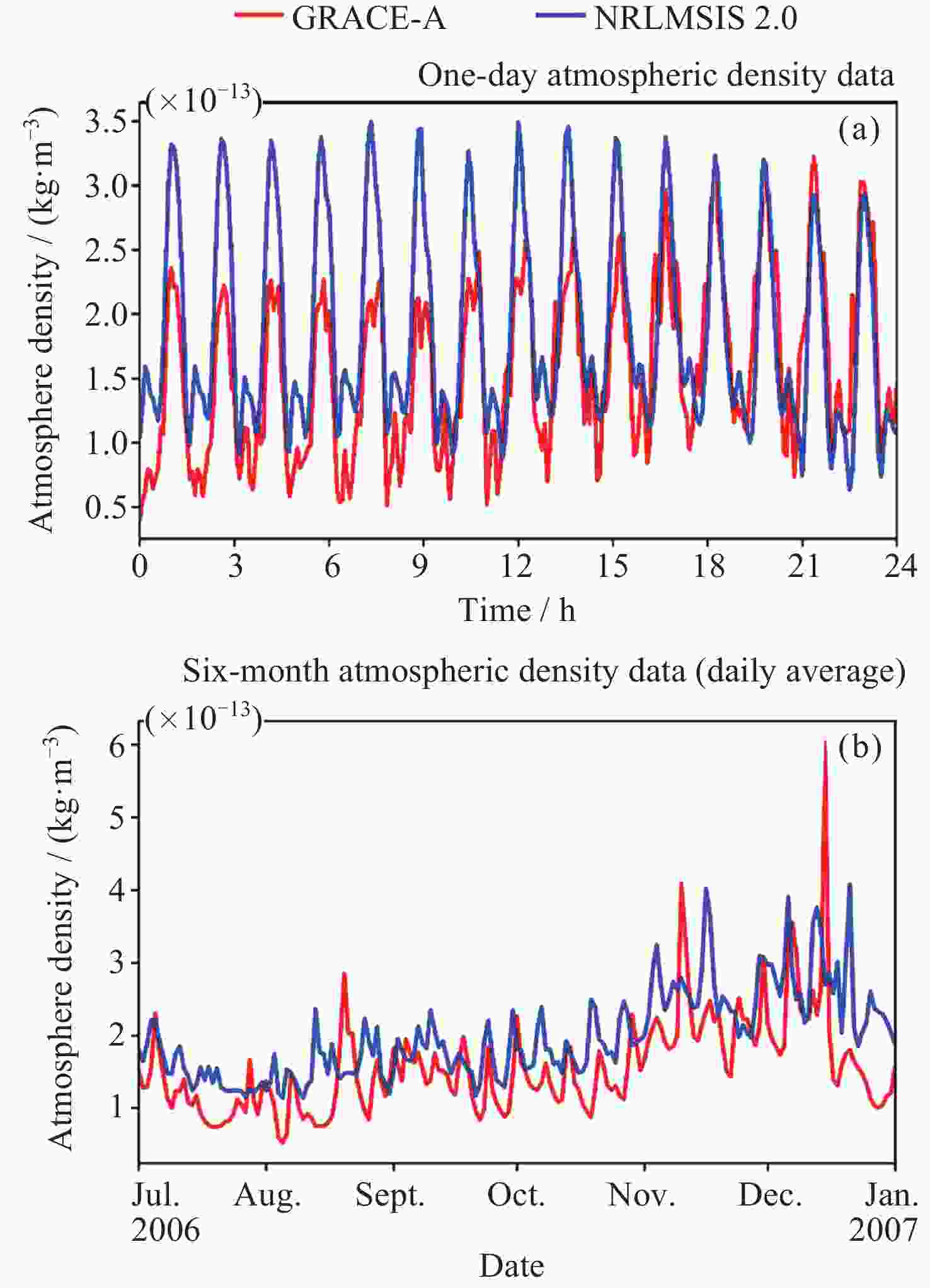
摘要: 大气阻力是低轨卫星受到的最大非引力摄动, 大气阻力的计算误差主要来源于热层大气密度经验模型误差, 目前经验模型的误差较大, 普遍在30%以上. 为提高经验模型的预报精度, 提出一种基于SegRNN (Segment Recurrent Neural Network)的热层大气密度经验模型校准方法. 该方法使用SegRNN的分块和并行策略进行模型训练和推理, 避免了传统RNN (Recurrent Neural Network)因迭代次数过多而引起误差累积与梯度不稳定的问题. 通过分析大气密度与Ap, F10.7和F10.7a外部环境参数的变化关系, 提出了一种改进的神经网络架构SegRNN with Residual Block. 该架构通过引入外部环境参数作为动态协变量(Covariates), 使用Residual Block (RB)提取预报时段的密度相关信息, 从而进一步提高SegRNN的预报精度. 利用GRACE (Gravity Recovery and Climate Experiment)星载加速度计反演得到的密度数据对NRLMSISE 2.0进行校准实验. 结果表明, NRLMSIS 2.0模型原始误差为31.3%, 经SegRNN校准后, 误差降低至8.0%, 引入动态协变量后, 模型误差进一步降低至7.2%, 最终校准模型误差下降了24.1%, 校准效果显著.
-
关键词:
- 大气密度 /
- 经验密度模型 /
- 神经网络 /
- 模型校准 /
- GRACE加速度计数据
Abstract: Atmospheric drag is the largest non-gravitational perturbation experienced by low-orbit satellites, and the main source of error in calculating atmospheric drag stems from inaccuracies in the empirical models of thermospheric density. Currently, these empirical models generally exhibit errors exceeding 30%. To enhance the prediction accuracy of these models, a calibration method for thermospheric density empirical models based on Segment Recurrent Neural Network (SegRNN) is proposed. This method employs the segmentation and parallelism strategies of SegRNN for model training and inference, mitigating the issues of error accumulation and gradient instability that arise from excessive iterations in traditional RNN. By analyzing the relationship between atmospheric density and external environmental parameters such as Ap, F10.7, and F10.7a, an improved neural network architecture named SegRNN with Residual Block is proposed. This architecture introduces external environmental parameters as dynamic covariates and employs a residual block to encode these covariates, thereby extracting density-related information for the prediction period and further enhancing the prediction accuracy of SegRNN. Finally, the density data derived from the onboard accelerometer of the GRACE (Gravity Recovery and Climate Experiment) satellite is used to calibrate the NRLMSIS 2.0 model. The results indicate that the original error of the NRLMSIS 2.0 model is 31.3%. After calibration with SegRNN, the error was reduced to 8.0%. By introducing dynamic covariates, the model error was further reduced to 7.2%. Ultimately, the error of the final calibrated model decreased by 24.1%, demonstrating significant calibration effects. -
图 1 NRLMSIS 2.0和GRACE-A加速度计反演的大气密度
Figure 1. Atmospheric density data obtained by NRLMSIS 2.0 and inversion from GRACE-A accelerometer
图 3 SegRNN with Residual Block模型结构
Figure 3. Model architecture of SegRNN with Residual Block
图 6 SegRNN和SegRNN with Residual Block模型预报结果
Figure 6. Prediction results of SegRNN and SegRNN with Residual Block model
图 8 NRLMSIS 2.0经验模型与SegRNN校准模型相对于GRCAE-A星载加速度密度数据的误差日均值
Figure 8. Daily average error of NRLMSIS 2.0 empirical model and SegRNN calibration model relative to GRCAE-A onboard acceleration density data
表 1 神经网络模型参数选择
Table 1. Neural network model parameter selection
Parameter Time/h 1 3 6 12 24 Seq len 768 768 768 768 768 Pred len 12 36 72 144 288 Seg len 6 12 12 48 96 Num layer 1 1 1 1 1 d model 256 256 512 512 1024 Dropout 0.5 0.5 0 0.5 0 Batch size 8 16 64 128 256 Epoch 30 30 30 30 30 Patience 6 6 6 6 6 Learning rate 0.0001 0.0001 0.0002 0.0002 0.0004 Loss function mse mse mse mse mse Optimizer Adam Adam Adam Adam Adam 
下载: 导出CSV
表 2 神经网络模型预报误差
Table 2. Prediction error of neural network models
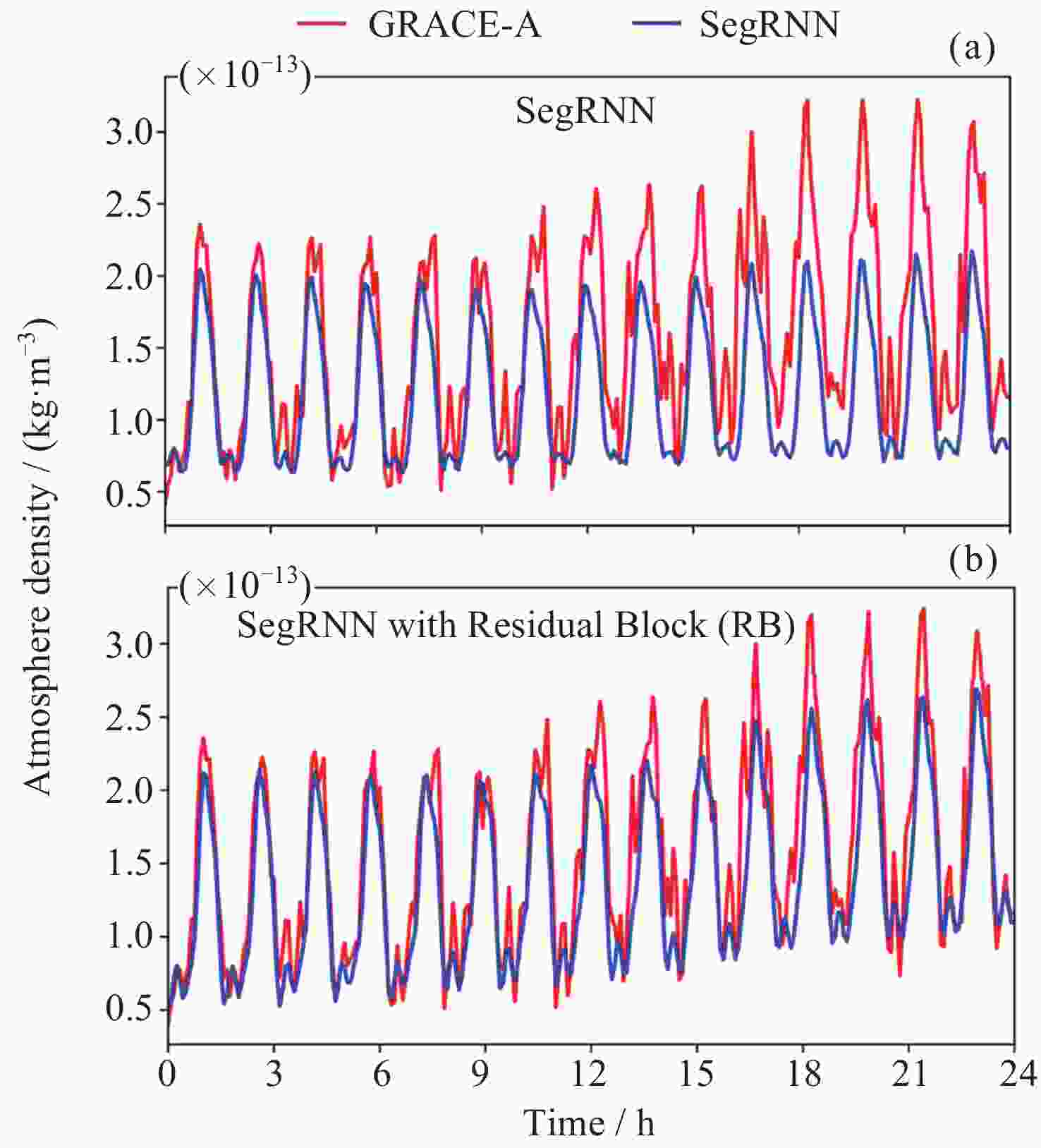
Horizon Metric Model LSTM SegRNN without RB SegRNN with RB 1 h RMSE/ (kg·m–3) 4.6×10–14 2.6×10–14 2.7×10–14 RE/(%) 7.8 4.7 2.5 3 h RMSE/(kg·m–3) 4.9×10–14 3.0×10–14 2.9×10–14 RE/(%) 8.2 4.7 4.3 6 h RMSE/(kg·m–3) 7.7×10–14 3.3×10–14 3.1×10–14 RE/(%) 14.8 7.4 4.2 12 h RMSE/(kg·m–3) 8.7×10–14 4.1×10–14 3.8×10–14 RE/(%) 17.2 7.8 4.4 24 h RMSE/(kg·m–3) 9.4×10–14 4.8×10–14 4.7×10–14 RE/(%) 17.4 8.0 7.2 注 RB为Residual Block model. RE为Relative Error. 黑体表示最小误差值.
下载: 导出CSV
-
[1] LI Min. Research on Muti-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan: Wuhan University, 2011: 63 [2] LIU Lin. Orbit Theory of Spacecraft[M]. Beijing: National Defense Industry Press, 2000 [3] MONTENBRUCK O, GILL E, LUTZE F. Satellite orbits: models, methods, and applications[J]. Applied Mechanics Reviews, 2002, 55(2): B27-B28 doi: 10.1115/1.1451162 [4] LIU Shushi, GONG J C, LIU S Q, et al. Thermospheric density during geomagnetic storm based on EOF analysis[J]. Chinese Journal of Geophysics, 2013, 56(10): 3236-3245 [5] JACCHIA L G. Revised static models of the thermosphere and exosphere with empirical temperature profiles[J]. Sao Special Report, 1971, 313(20): 3138-3144 [6] PICONE J M, HEDIN A E, DROB D P, et al. NRLMSISE-00 empirical model of the atmosphere: statistical comparisons and scientific issues[J]. Journal of Geophysical Research, Space Physics, 2002, 107(A12): SIA 15-1-SIA 15-16 [7] BRUINSMA S. The DTM-2013 thermosphere model[J]. Journal of Space Weather and Space Climate, 2015, 5: A1 doi: 10.1051/swsc/2015001 [8] BRUINSMA S, THUILLIER G, BARLIER F. The DTM-2000 empirical thermosphere model with new data assimilation and constraints at lower boundary: accuracy and properties[J]. Journal of Atmospheric and Solar Terrestrial Physics, 2003, 65(9): 1053-1070 doi: 10.1016/S1364-6826(03)00137-8 [9] BOWMAN B R, TOBISKA W K, MARCOS F A. A new empirical thermospheric density model JB2006 using new solar indices[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Keystone: AIAA, 2006: 6166 [10] BOWMAN B R, TOBISKA W K, MARCOS F A, et al. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu: AIAA, 2008: 6438 [11] EMMERT J T. Thermospheric mass density: a review[J]. Advances in Space Research, 2015, 56(5): 773-824 doi: 10.1016/j.asr.2015.05.038 [12] STORZ M F, BOWMAN B R, BRANSON M J I, et al. High accuracy satellite drag model(HASDM)[J]. Advances in Space Research, 2005, 36(12): 2497-2505 doi: 10.1016/j.asr.2004.02.020 [13] CASALI S J, BARKER W N. Dynamic Calibration Atmosphere (DCA) for the high accuracy satellite drag model (HASDM)[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Monterey: AIAA, 2013. DOI: 10.2514/6.2002-4888 [14] LI Wenwen, LI Min, SHI Chuang, et al. Thermosphere mass density derivation using on-board accelerometer observations from GRACE satellites[J]. Chinese Journal of Geophysics, 2016, 59(9): 3159-3174 [15] DOORNBOS E, KLINKRAD H, VISSER P. Atmospheric density calibration using satellite drag observations[J]. Advances in Space Research, 2005, 36(3): 515-521 doi: 10.1016/j.asr.2005.02.009 [16] CEFOLA P J, PROULX R J, NAZARENKO A I, et al. Atmospheric density correction using two line element sets as the observation data[J]. Advances in the Astronautical Sciences, 2004, 116: 1953-1978 [17] BERGSTROM S E, PROULX R J, CEFOLA P J. Atmospheric density correction using observational data[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Monterey: AIAA, 2002: 4738 [18] CHEN Xuxing, HU Xiong, XIAO Chunying, et al. Correction method of the low earth orbital neutral density prediction based on the satellites data and NRLMSISE-00 model[J]. Chinese Journal of Geophysics, 2013, 56(10): 3246-3254 [19] PÉREZ D, BEVILACQUA R. Neural Network based calibration of atmospheric density models[J]. Acta Astronautica, 2015, 110: 58-76 doi: 10.1016/j.actaastro.2014.12.018 [20] PÉREZ D, WOHLBERG B, LOVELL T A, et al. Orbit-centered atmospheric density prediction using artificial neural networks[J]. Acta Astronautica, 2014, 98: 9-23 doi: 10.1016/j.actaastro.2014.01.007 [21] CHEN H R, LIU H X, HANADA T. Storm-time atmospheric density modeling using neural networks and its application in orbit propagation[J]. Advances in Space Research, 2014, 53(3): 558-567 doi: 10.1016/j.asr.2013.11.052 [22] ZHANG Y, YU J J, CHEN J Y, et al. An empirical atmospheric density calibration model based on long short-term memory neural network[J]. Atmosphere, 2021, 12(7): 925 doi: 10.3390/atmos12070925 [23] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780 doi: 10.1162/neco.1997.9.8.1735 [24] ZHOU H Y, ZHANG S H, PENG J Q, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting[C]//Proceedings of the 35th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2021: 11106-11115 [25] LIN S S, LIN W W, WU W T, et al. SegRNN: Segment recurrent neural network for long-term time series forecasting[OL]. (2023-08-22) [2024.12.30]. https://arxiv.org/abs/2308.11200 [26] EMMERT J T, DROB D P, PICONE J M, et al. NRLMSIS 2.0: a whole‐atmosphere empirical model of temperature and neutral species densities[J]. Earth and Space Science, 2021, 8(3): e2020EA001321 doi: 10.1029/2020EA001321 [27] VAN DEN IJSSEL J, VISSER P. Performance of GPS-based accelerometry: CHAMP and GRACE[J]. Advances in Space Research, 2007, 39(10): 1597-1603 doi: 10.1016/j.asr.2006.12.027 [28] TAPPING K F. The 10.7 cm solar radio flux (F10.7)[J]. Space Weather-the International Journal of Research :Times New Roman;">& Applications, 2013, 11(7): 394-406 [29] BARTELS J. The geomagnetic measures for the time-variations of solar corpuscular radiation, described for use in correlation studies in other geophysical fields[J]. Geomagnetism, 2013: 227-236 [30] KNIPP D J, TOBISKA W K, EMERY B A. Direct and indirect thermospheric heating sources for solar cycles 21-23[J]. Solar Physics, 2004, 224(1/2): 495-505 [31] GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[J]. Journal of Machine Learning Research, 2011, 15: 315-323 [32] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1): 1929-1958 [33] WU D X, WANG Y S, XIA S T, et al. Skip connections matter: On the transferability of adversarial examples generated with resnets[OL]. (2020-02-14) [2024.12. 30]. https://arxiv.org/abs/2002.05990 [34] PASZKE A, GROSS S, MASSA F, et al. Pytorch: an imperative style, high-performance deep learning library[J]. Neural Information Processing Systems, 2019, 32: 8026-8037 [35] CHUNG J Y, GULCEHRE C, CHO K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. Eprint Arxiv, 2014. DOI: 10.48550/arXiv.1412.3555 [36] KINGMA D P, BA J. Adam: A method for stochastic optimization[OL]. (2017-01-30) [2024-12-25]. https://arxiv.org/abs/1412.6980 [37] HAN L, YE H J, ZHAN D C. The capacity and robustness trade-off: Revisiting the channel independent strategy for multivariate time series forecasting[J]. IEEE Transactions on Automatic Control, 2024, 36(11): 7129-7142 [38] WANG Hongbo, ZHANG Mingjiang, XIONG Jianning. Effects of solar extreme ultraviolet radiation on thermospheric neutral density[J]. Chinese Journal of Space Science, 2023, 43(1): 87-100 (汪宏波, 张明江, 熊建宁. 太阳极紫外辐射对热层大气密度的影响[J]. 空间科学学报, 2023, 43(1): 87-100 doi: 10.11728/cjss2023.01.211217130WANG Hongbo, ZHANG Mingjiang, XIONG Jianning. Effects of solar extreme ultraviolet radiation on thermospheric neutral density[J]. Chinese Journal of Space Science, 2023, 43(1): 87-100 doi: 10.11728/cjss2023.01.211217130 [39] WANG Xin, MIAO Juan, LIU Siqing, et al. Characteristics analysis of thermospheric density response during the different intensity of geomagnetic storms[J]. Chinese Journal of Space Science, 2020, 40(1): 28-41 (王昕, 苗娟, 刘四清, 等. 不同强度磁暴期间热层大气密度响应特征分析[J]. 空间科学学报, 2020, 40(1): 28-41 doi: 10.11728/cjss2020.01.028WANG Xin, MIAO Juan, LIU Siqing, et al. Characteristics analysis of thermospheric density response during the different intensity of geomagnetic storms[J]. Chinese Journal of Space Science, 2020, 40(1): 28-41 doi: 10.11728/cjss2020.01.028 -
-
下载:
图(8) / 表(2)
计量
- 文章访问数: 387
- HTML全文浏览量: 74
- PDF下载量: 14
-
被引次数:
0(来源:Crossref)
0(来源:其他)
